3.2.4 立体几何中的向量方法 课件1
文档属性
| 名称 | 3.2.4 立体几何中的向量方法 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 20:35:53 | ||
图片预览

文档简介
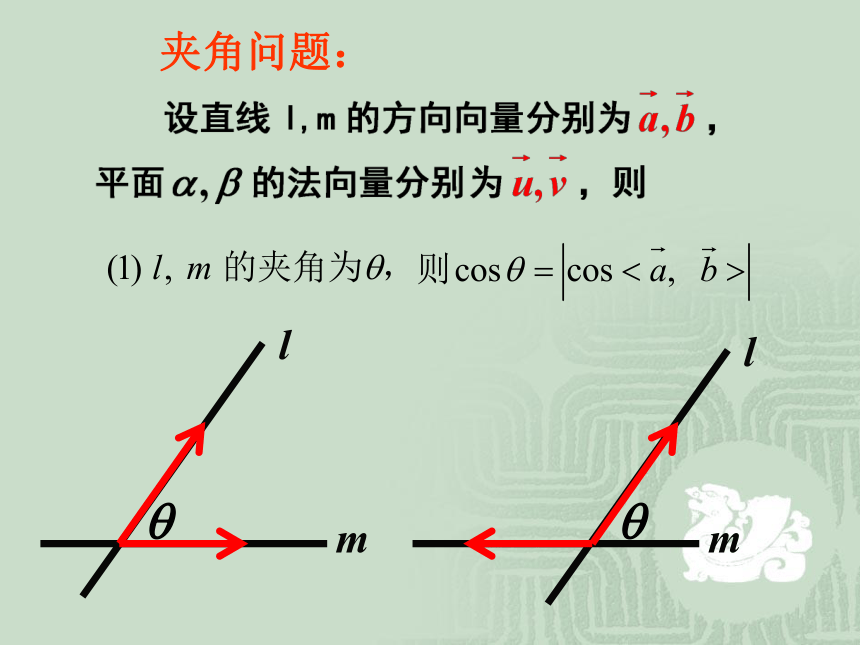
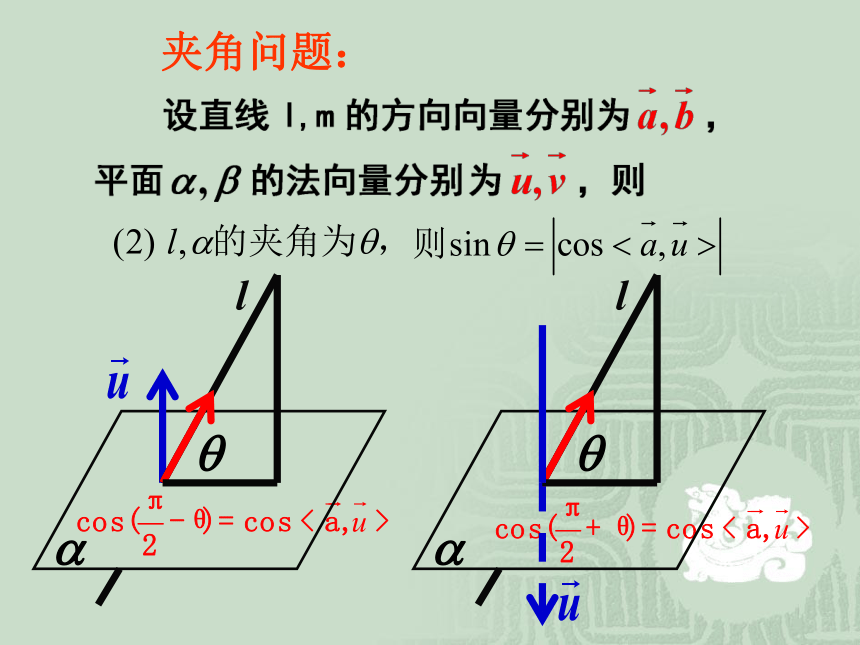
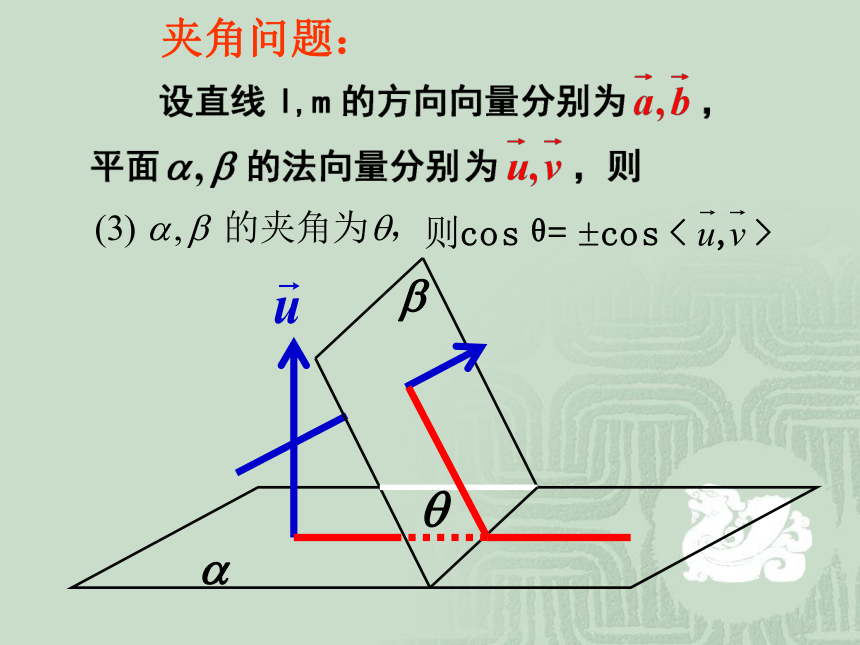
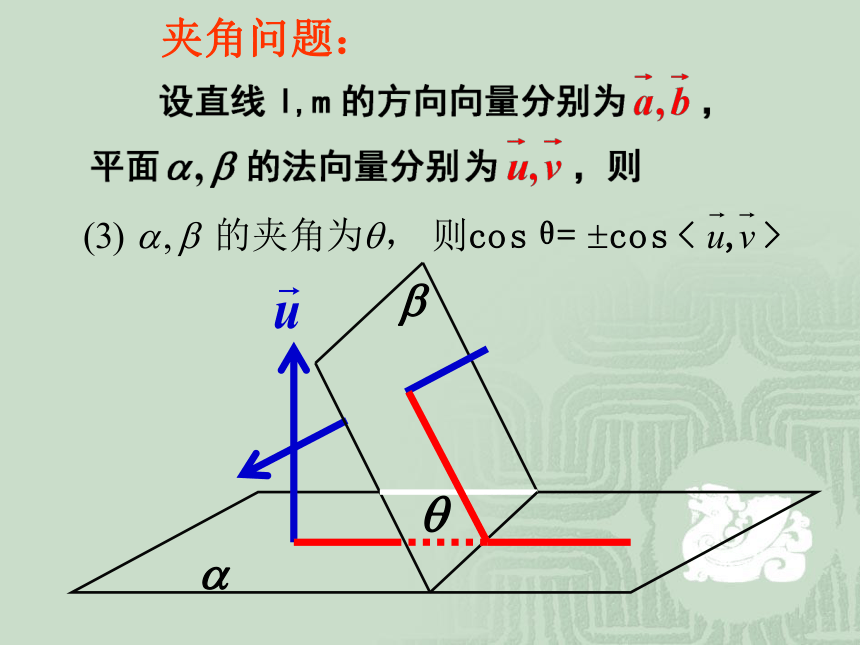
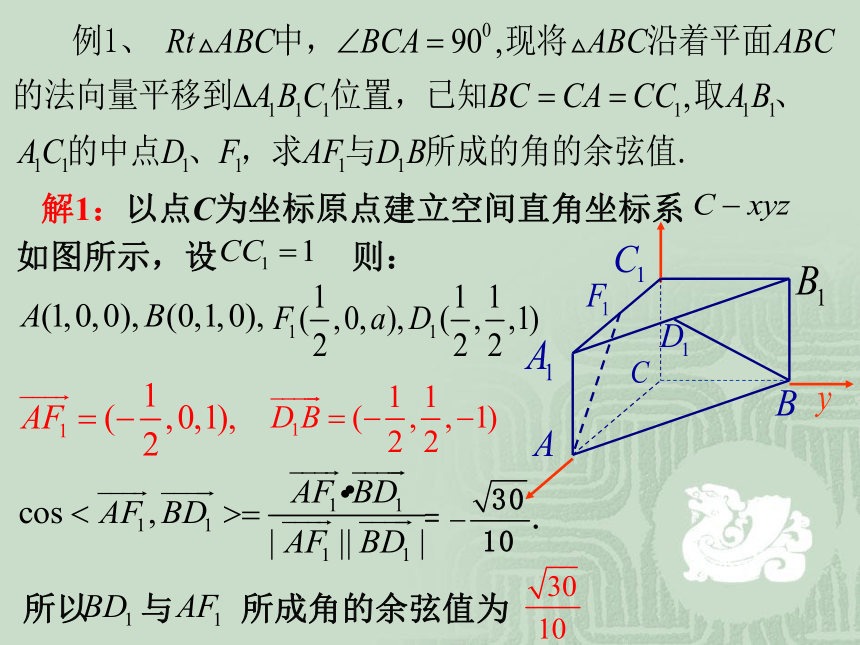
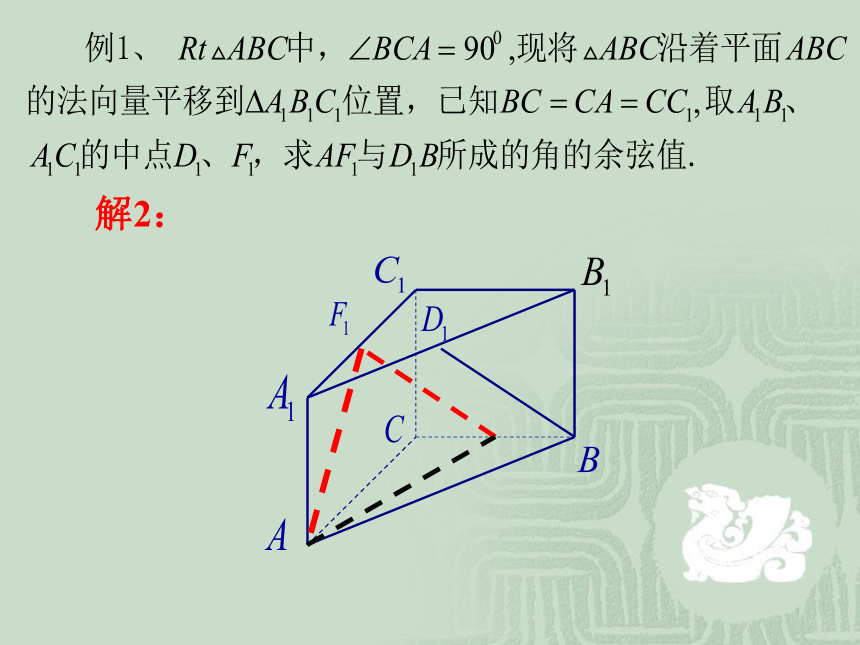
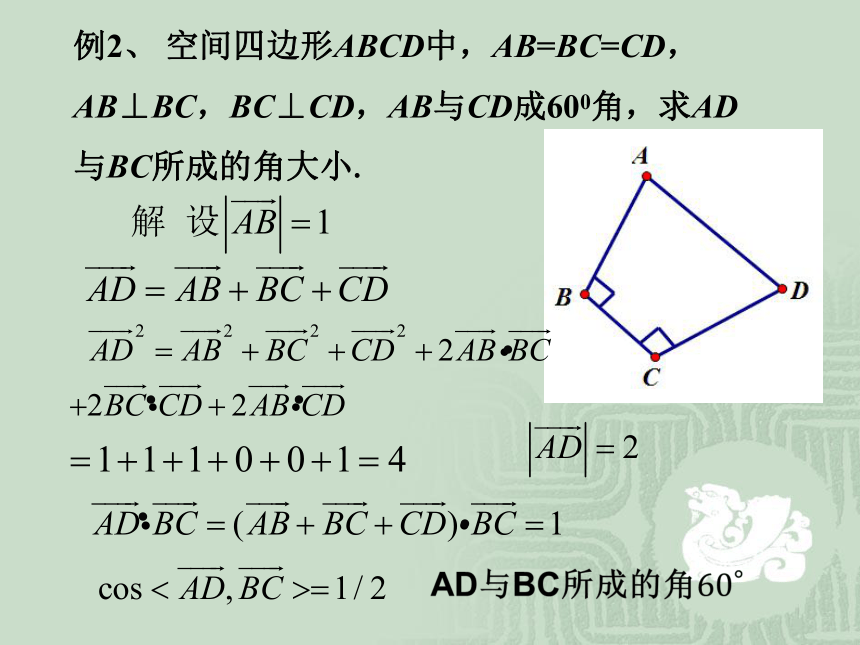
课件22张PPT。第三章 空间向量与立体几何3.2.4 立体几何中的向量方法夹角问题:lm夹角问题:ll夹角问题:夹角问题:.解2:例2、 空间四边形ABCD中,AB=BC=CD,
AB⊥BC,BC⊥CD,AB与CD成600角,求AD
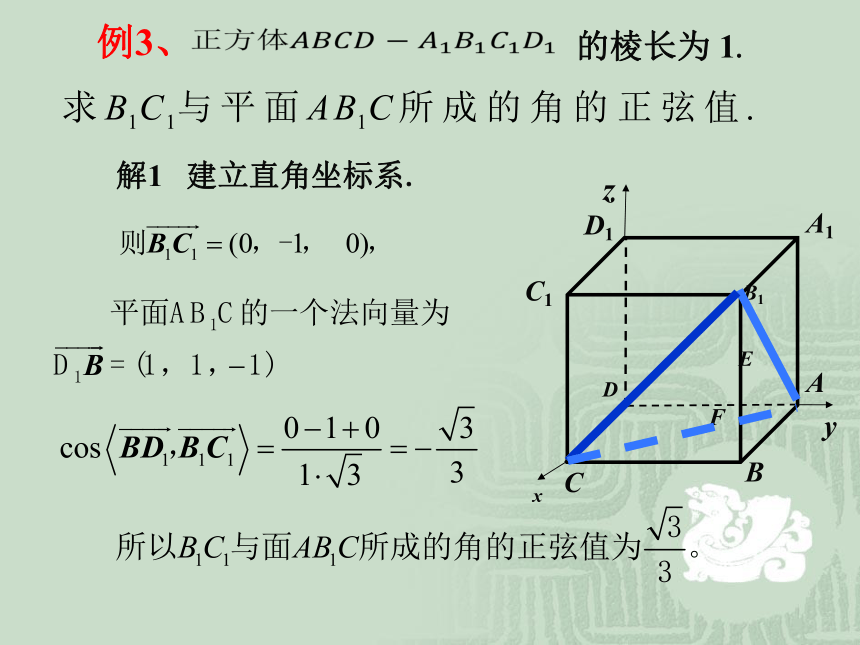
与BC所成的角大小.?.....例3、
解1 建立直角坐标系.?例3、解2 ? 例4、 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D
的大小.ABCDPEFABCDPEF(3) 解 建立空间直角坐标系,设DC=1. 例4、 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D
的大小.ABCDPEF平面PBC的一个法向量为 解2 如图所示建立
空间直角坐标系,设DC=1.平面PBD的一个法向量为G 例4、 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D
的大小.ABCDPEF 解3 设DC=1.例5、 解1 建立直角坐标系.?平面PBD1的一个法向量为平面CBD1的一个法向量为解2?例5、 距离问题:(1) A(x1,y1,z1), B(x2,y2,z2), 则距离问题:(2) 点P与直线l的距离为d , 则距离问题:(3) 点P与平面α的距离为d , 则d距离问题:(4) 平面α与β的距离为d , 则
AB⊥BC,BC⊥CD,AB与CD成600角,求AD
与BC所成的角大小.?.....例3、
解1 建立直角坐标系.?例3、解2 ? 例4、 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D
的大小.ABCDPEFABCDPEF(3) 解 建立空间直角坐标系,设DC=1. 例4、 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D
的大小.ABCDPEF平面PBC的一个法向量为 解2 如图所示建立
空间直角坐标系,设DC=1.平面PBD的一个法向量为G 例4、 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F. (3)求二面角C-PB-D
的大小.ABCDPEF 解3 设DC=1.例5、 解1 建立直角坐标系.?平面PBD1的一个法向量为平面CBD1的一个法向量为解2?例5、 距离问题:(1) A(x1,y1,z1), B(x2,y2,z2), 则距离问题:(2) 点P与直线l的距离为d , 则距离问题:(3) 点P与平面α的距离为d , 则d距离问题:(4) 平面α与β的距离为d , 则
