3.2.4 立体几何中的向量方法 课件3
文档属性
| 名称 | 3.2.4 立体几何中的向量方法 课件3 |  | |
| 格式 | zip | ||
| 文件大小 | 567.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 21:32:03 | ||
图片预览


文档简介
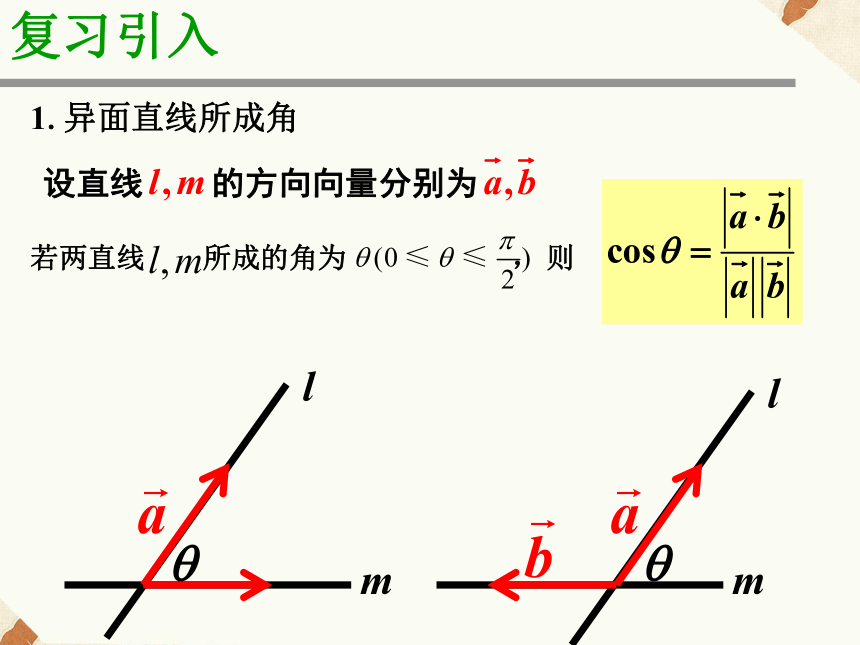
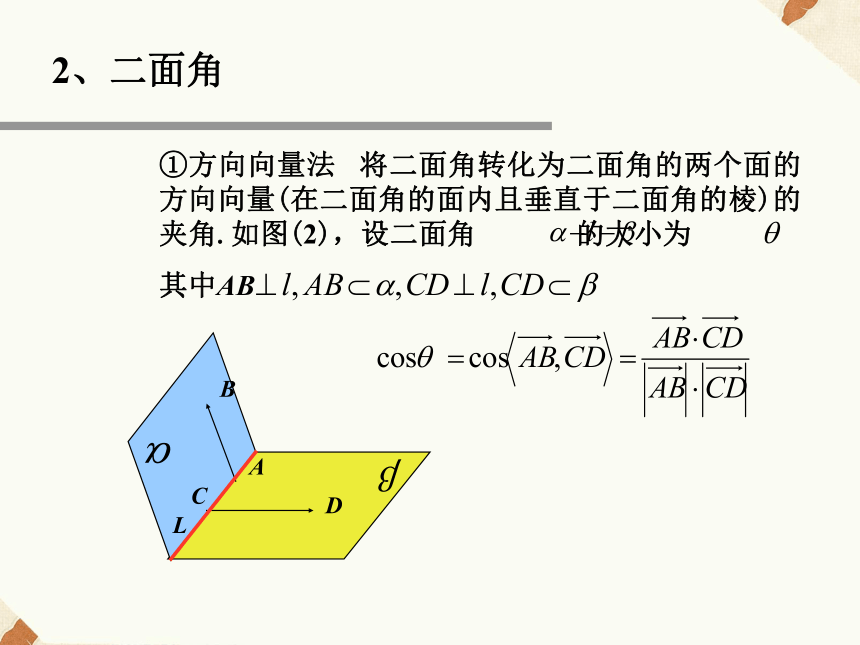
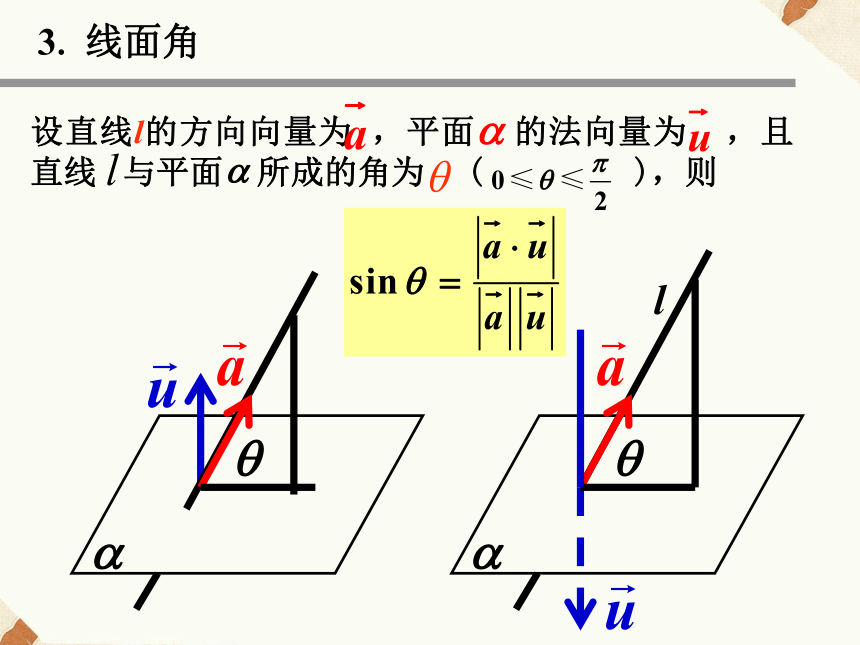
课件15张PPT。3.2.4立体几何中的向量方法空间“角度”问题1.异面直线所成角lmlm若两直线 所成的角为 , 则复习引入①方向向量法 将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角.如图(2),设二面角 的大小为
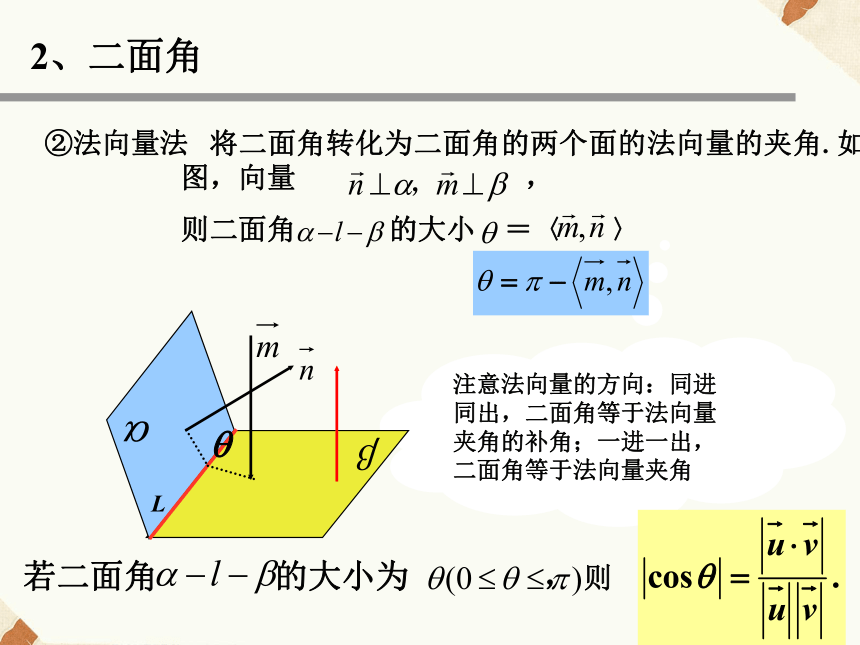
其中AB 2、二面角注意法向量的方向:同进同出,二面角等于法向量夹角的补角;一进一出,二面角等于法向量夹角 将二面角转化为二面角的两个面的法向量的夹角.如图,向量 ,
则二面角 的大小 =〈 〉
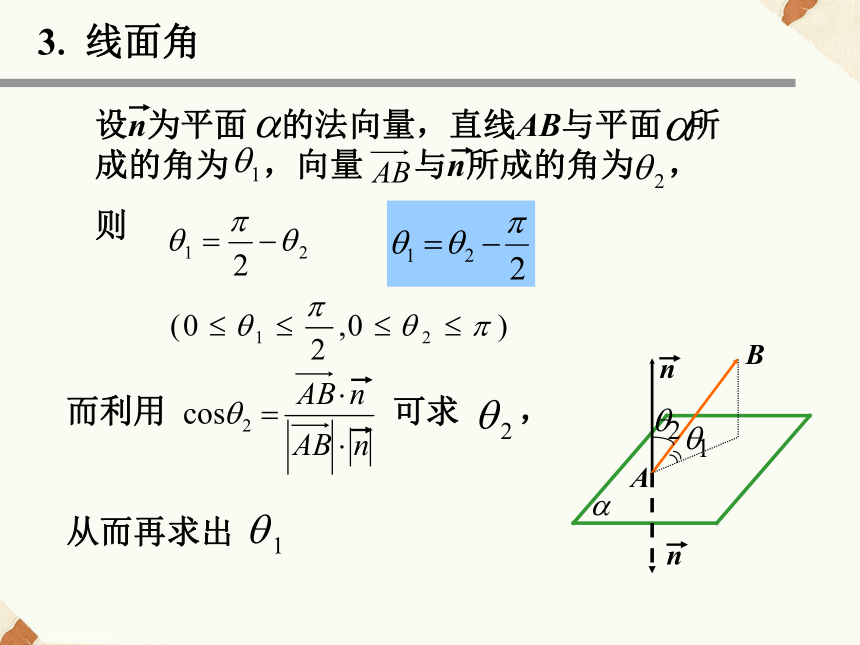
2、二面角若二面角 的大小为 , 则②法向量法3. 线面角3. 线面角l设直线l的方向向量为 ,平面 的法向量为 ,且直线 与平面 所成的角为 ( ),则2、如果平面的一条斜线与它在这个平面上的射影的方向向量分别是a=(1,0,1),b=(0,1,1),那么这条斜线与平面所成的角是______ .3、已知两平面的法向量分别m=(0,1,0),n=(0,1,1),则两平面所成的钝二面角为______ .基础训练:1、已知 =(2,2,1), =(4,5,3),则平面ABC的一个法向量是______ .6001350N解:如图建立坐标系A-xyz,则N又例2、如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC 底面ABCD.已知 AB=2,BC= ,SA=SB= .
(1)求证
(2)求直线SD与平面SAB所成角的正弦值.SABCD【典例剖析】 例3 如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,PA=AB=1,AD= ,在线段BC上是否存在一点E,使PA与平面PDE所成角的大小为450? 若存在,确定点E的位置;若不存在说明理由. 【典例剖析】 DBACEP解:以A为原点,AD、AB、AP所在的直线分别为X轴、Y轴、Z轴,建立空间直角坐标系,设BE=m,则例4、(2004,天津)如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD 底面ABCD,PD=DC,E是PC的中点.
(1)证明:PA//平面EDB;
(2)求EB与底面ABCD所成的角的正切值.【典例剖析】 ABCDPE【巩固练习】 1 三棱锥P-ABC PA⊥ABC,PA=AB=AC,
,E为PC中点 ,则PA与BE所成角的余弦值为_________ .
2 直三棱柱ABC-A1B1C1中A1A=2, AB=AC=1, 则AC1与截面BB1CC1所成
角的余弦值为_________ .
3正方体中ABCD-A1B1C1D1中E为A1D1的
中点, 则二面角E-BC-A的大小是_________如图,已知:直角梯形OABC中,OA∥BC,∠AOC=90°,SO⊥面OABC,且OS=OC=BC=1,OA=2.求:
(1)异面直线SA和OB所成的角的余弦值
(2)OS与面SAB所成角的余弦值
(3)二面角B-AS-O的余弦值【课后作业】
其中AB 2、二面角注意法向量的方向:同进同出,二面角等于法向量夹角的补角;一进一出,二面角等于法向量夹角 将二面角转化为二面角的两个面的法向量的夹角.如图,向量 ,
则二面角 的大小 =〈 〉
2、二面角若二面角 的大小为 , 则②法向量法3. 线面角3. 线面角l设直线l的方向向量为 ,平面 的法向量为 ,且直线 与平面 所成的角为 ( ),则2、如果平面的一条斜线与它在这个平面上的射影的方向向量分别是a=(1,0,1),b=(0,1,1),那么这条斜线与平面所成的角是______ .3、已知两平面的法向量分别m=(0,1,0),n=(0,1,1),则两平面所成的钝二面角为______ .基础训练:1、已知 =(2,2,1), =(4,5,3),则平面ABC的一个法向量是______ .6001350N解:如图建立坐标系A-xyz,则N又例2、如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC 底面ABCD.已知 AB=2,BC= ,SA=SB= .
(1)求证
(2)求直线SD与平面SAB所成角的正弦值.SABCD【典例剖析】 例3 如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,PA=AB=1,AD= ,在线段BC上是否存在一点E,使PA与平面PDE所成角的大小为450? 若存在,确定点E的位置;若不存在说明理由. 【典例剖析】 DBACEP解:以A为原点,AD、AB、AP所在的直线分别为X轴、Y轴、Z轴,建立空间直角坐标系,设BE=m,则例4、(2004,天津)如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD 底面ABCD,PD=DC,E是PC的中点.
(1)证明:PA//平面EDB;
(2)求EB与底面ABCD所成的角的正切值.【典例剖析】 ABCDPE【巩固练习】 1 三棱锥P-ABC PA⊥ABC,PA=AB=AC,
,E为PC中点 ,则PA与BE所成角的余弦值为_________ .
2 直三棱柱ABC-A1B1C1中A1A=2, AB=AC=1, 则AC1与截面BB1CC1所成
角的余弦值为_________ .
3正方体中ABCD-A1B1C1D1中E为A1D1的
中点, 则二面角E-BC-A的大小是_________如图,已知:直角梯形OABC中,OA∥BC,∠AOC=90°,SO⊥面OABC,且OS=OC=BC=1,OA=2.求:
(1)异面直线SA和OB所成的角的余弦值
(2)OS与面SAB所成角的余弦值
(3)二面角B-AS-O的余弦值【课后作业】
