3.2.5 立体几何中的向量方法 课件1
文档属性
| 名称 | 3.2.5 立体几何中的向量方法 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 945.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 00:00:00 | ||
图片预览






文档简介
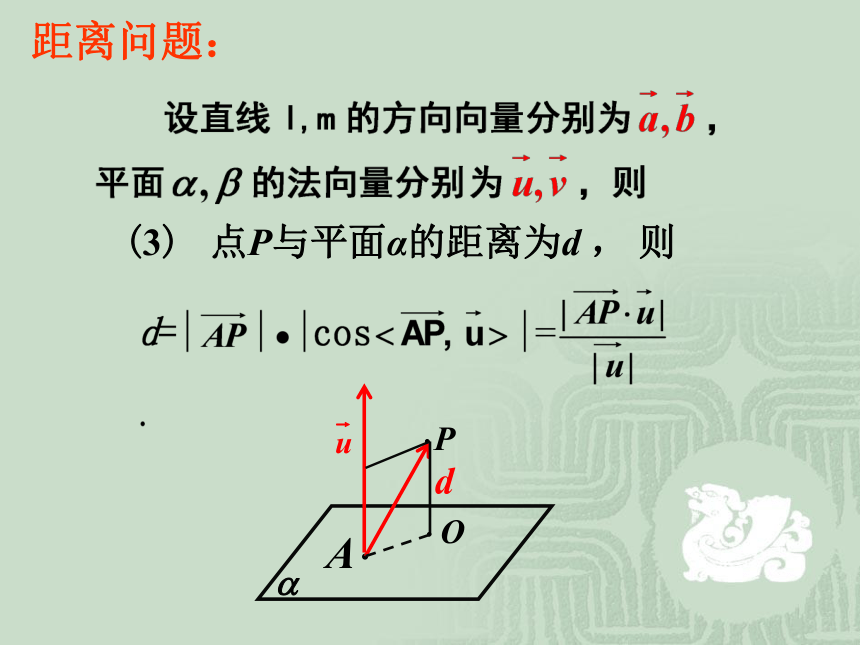
课件25张PPT。第三章 空间向量与立体几何3.2.5 立体几何中的向量方法距离问题:(1) A(x1,y1,z1), B(x2,y2,z2), 则距离问题:(2) 点P与直线l的距离为d , 则距离问题:(3) 点P与平面α的距离为d , 则d距离问题:(4) 平面α与β的距离为d , 则 例1、 如图1:一个结晶体的形状为四棱柱,其中,以顶点A为端点
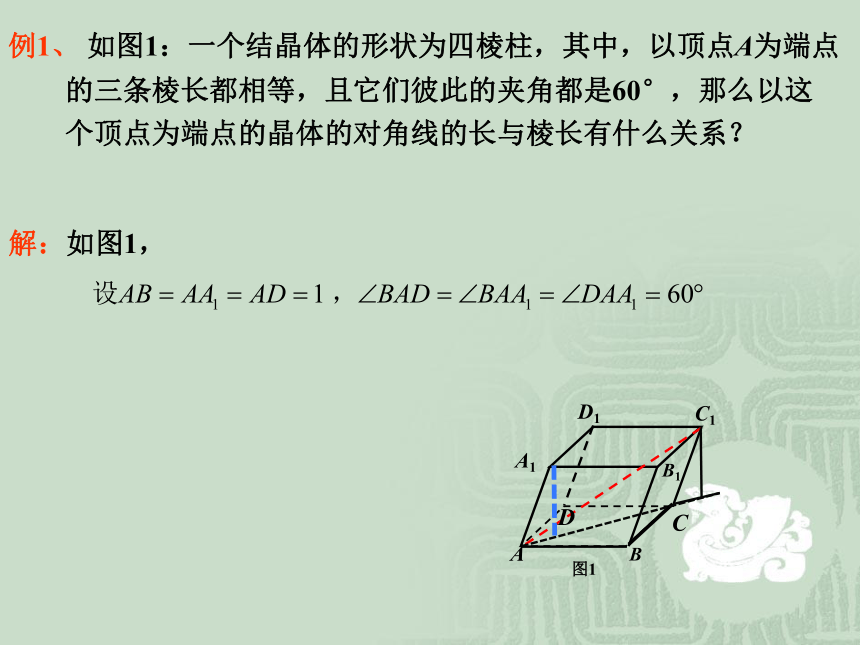
的三条棱长都相等,且它们彼此的夹角都是60°,那么以这
个顶点为端点的晶体的对角线的长与棱长有什么关系? 解:如图1,所以答: 这个晶体的对角线
AC1 的长是棱长的 倍. 例1、 如图1:一个结晶体的形状为四棱柱,其中,以顶点A为端点
的三条棱长都相等,且它们彼此的夹角都是60°,那么以这
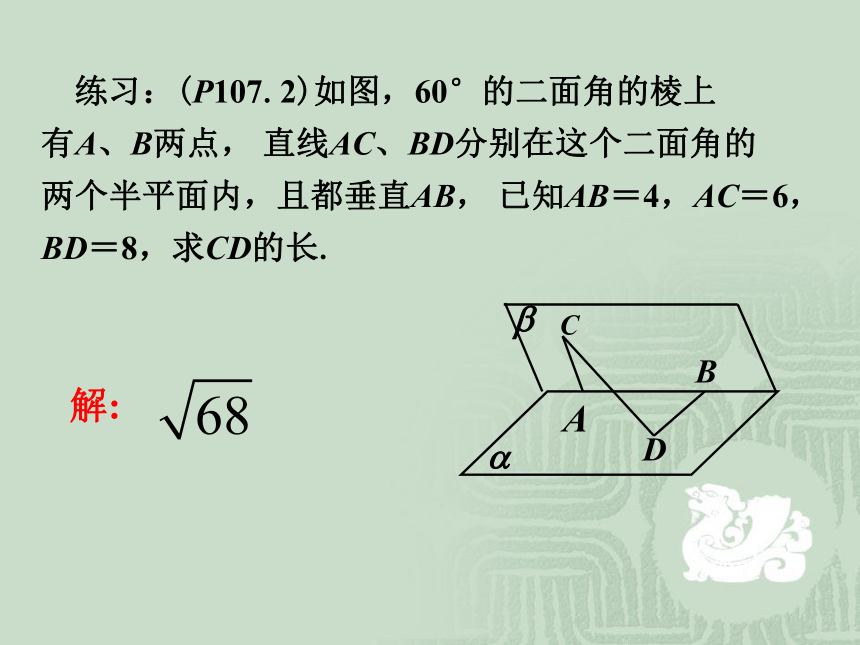
个顶点为端点的晶体的对角线的长与棱长有什么关系? 解:如图1, 练习:(P107.2)如图,60°的二面角的棱上
有A、B两点, 直线AC、BD分别在这个二面角的
两个半平面内,且都垂直AB, 已知AB=4,AC=6,
BD=8,求CD的长. 解: 练习:(P107.2)如图,60°的二面角的棱上
有A、B两点, 直线AC、BD分别在这个二面角的
两个半平面内,且都垂直AB, 已知AB=4,AC=6,
BD=8,求CD的长. 解2 例2、 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求点E到直线A1B的距离.点E到直线A1B的距离为 例2、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求点E到直线A1B的距离.解: 例3、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求B1到面A1BE的距离.... 例3、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求B1到面A1BE的距离.等体积法解2 例4、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求D1C到面A1BE的距离. 解1:∵D1C∥面A1BE
∴ D1到面A1BE的距离即为
D1C到面A1BE的距离. 仿上例求得D1C到 面A1BE的距离为 例4、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求D1C到面A1BE的距离.等体积法解2 例5、如图,在正方体ABCD-A1B1C1D1中,棱长为1,求面A1DB与面D1CB1的距离. 解1:∵面D1CB1∥面A1BD
∴ D1到面A1BD的距离即
为面D1CB1到面A1BD的距离 例5、如图,在正方体ABCD-A1B1C1D1中,棱长为1,求面A1DB与面D1CB1的距离.等体积法解2 例5、如图,在正方体ABCD-A1B1C1D1中,棱长为1,求面A1DB与面D1CB1的距离.解3 例6、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求异面直线D1B与A1E的距离. 例7、如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线l(库底与水坝的交线)的距离AC和BD分别为a 和b ,CD的长为c, AB的长为d .求库底与水坝所成二面角的余弦值. 解1:如图,答:…解2:如图, 例7、如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线l(库底与水坝的交线)的距离AC和BD分别为a 和b ,CD的长为c, AB的长为d .求库底与水坝所成二面角的余弦值. 例8、如图,一块均匀的正三角形面的钢板的质量为 ,在它的顶点处分别受力 、 、 ,每个力与同它相邻的三角形的两边之间的夹角都是 ,且 .这块钢板在这些力的作用下将会怎样运动?这三个力最小为多大时,才能提起这块钢板? 根据对称性可知
的三条棱长都相等,且它们彼此的夹角都是60°,那么以这
个顶点为端点的晶体的对角线的长与棱长有什么关系? 解:如图1,所以答: 这个晶体的对角线
AC1 的长是棱长的 倍. 例1、 如图1:一个结晶体的形状为四棱柱,其中,以顶点A为端点
的三条棱长都相等,且它们彼此的夹角都是60°,那么以这
个顶点为端点的晶体的对角线的长与棱长有什么关系? 解:如图1, 练习:(P107.2)如图,60°的二面角的棱上
有A、B两点, 直线AC、BD分别在这个二面角的
两个半平面内,且都垂直AB, 已知AB=4,AC=6,
BD=8,求CD的长. 解: 练习:(P107.2)如图,60°的二面角的棱上
有A、B两点, 直线AC、BD分别在这个二面角的
两个半平面内,且都垂直AB, 已知AB=4,AC=6,
BD=8,求CD的长. 解2 例2、 如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求点E到直线A1B的距离.点E到直线A1B的距离为 例2、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求点E到直线A1B的距离.解: 例3、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求B1到面A1BE的距离.... 例3、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求B1到面A1BE的距离.等体积法解2 例4、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求D1C到面A1BE的距离. 解1:∵D1C∥面A1BE
∴ D1到面A1BE的距离即为
D1C到面A1BE的距离. 仿上例求得D1C到 面A1BE的距离为 例4、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求D1C到面A1BE的距离.等体积法解2 例5、如图,在正方体ABCD-A1B1C1D1中,棱长为1,求面A1DB与面D1CB1的距离. 解1:∵面D1CB1∥面A1BD
∴ D1到面A1BD的距离即
为面D1CB1到面A1BD的距离 例5、如图,在正方体ABCD-A1B1C1D1中,棱长为1,求面A1DB与面D1CB1的距离.等体积法解2 例5、如图,在正方体ABCD-A1B1C1D1中,棱长为1,求面A1DB与面D1CB1的距离.解3 例6、如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求异面直线D1B与A1E的距离. 例7、如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线l(库底与水坝的交线)的距离AC和BD分别为a 和b ,CD的长为c, AB的长为d .求库底与水坝所成二面角的余弦值. 解1:如图,答:…解2:如图, 例7、如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线l(库底与水坝的交线)的距离AC和BD分别为a 和b ,CD的长为c, AB的长为d .求库底与水坝所成二面角的余弦值. 例8、如图,一块均匀的正三角形面的钢板的质量为 ,在它的顶点处分别受力 、 、 ,每个力与同它相邻的三角形的两边之间的夹角都是 ,且 .这块钢板在这些力的作用下将会怎样运动?这三个力最小为多大时,才能提起这块钢板? 根据对称性可知
