6.2角 同步练习含答案

6.2
角
一．选择题
1．如图所示，用量角器度量∠AOB，可以读出∠AOB的度数为（　　）
A．45°
B．55°
C．125°
D．135°
2．下列关系式正确的是（　　）
A．35.5°=35°5′
B．35.5°=35°50′
C．35.5°＜35°5′
D．35.5°＞35°5′
3．如图，Rt△ABC的斜边AB与量角器的直径恰好重合，B点与0刻度线的一端重合，∠ABC=40°，射线CD绕点C转动，与量角器外沿交于点D，若射线CD将△ABC分割出以BC为边的等腰三角形，则点D在量角器上对应的度数是（　　）
A．40°
B．70°
C．70°或80°
D．80°或140°
4．已知∠AOB=70°，以O为端点作射线OC，使∠AOC=42°，则∠BOC的度数为（　　）
A．28°
B．112°
C．28°或112°
D．68°
5．如果从甲船看乙船，乙船在甲船的北偏东30°方向，那么从乙船看甲船，甲船在乙船的（　　）
A．南偏西30°方向
B．南偏西60°方向
C．南偏东30°方向
D．南偏东60°方向
6．如图，在A、B
两地之间要修一条笔直的公路，从A地测得公路走向是北偏东48°，A，B两地同时开工，若干天后公路准确接通，若公路AB长8千米，另一条公路BC长是6千米，且BC的走向是北偏西42°，则A地到公路BC的距离是（　　）
A．6千米
B．8千米
C．10千米
D．14千米
7．一艘海上搜救船借助雷达探测仪寻找到事故船的位置，雷达示意图如图所示，搜救船位于图中圆心O处，事故船位于距O点40海里的A处，雷达操作员要用方位角把事故船相对于搜救船的位置汇报给船长，以便调整航向，下列四种表述方式中正确的为（　　）
A．事故船在搜救船的北偏东60°方向
B．事故船在搜救船的北偏东30°方向
C．事故船在搜救船的北偏西60°方向
D．事故船在搜救船的南偏东30°方向
8．如图，在一次定向越野活动中，“超越”小组准备从目前所在的A
处前往相距2km的B处，则相对于A处来说，B处的位置是（　　）
A．南偏西50°，2km
B．南偏东50°，2km
C．北偏西40°，2km
D．北偏东40°，2km
　
二．填空题
9．1.45°=　　．
10．北偏东30°与南偏东50°的两条射线组成的角的度数为　　°．
11．计算33°52′+21°54′=　　．
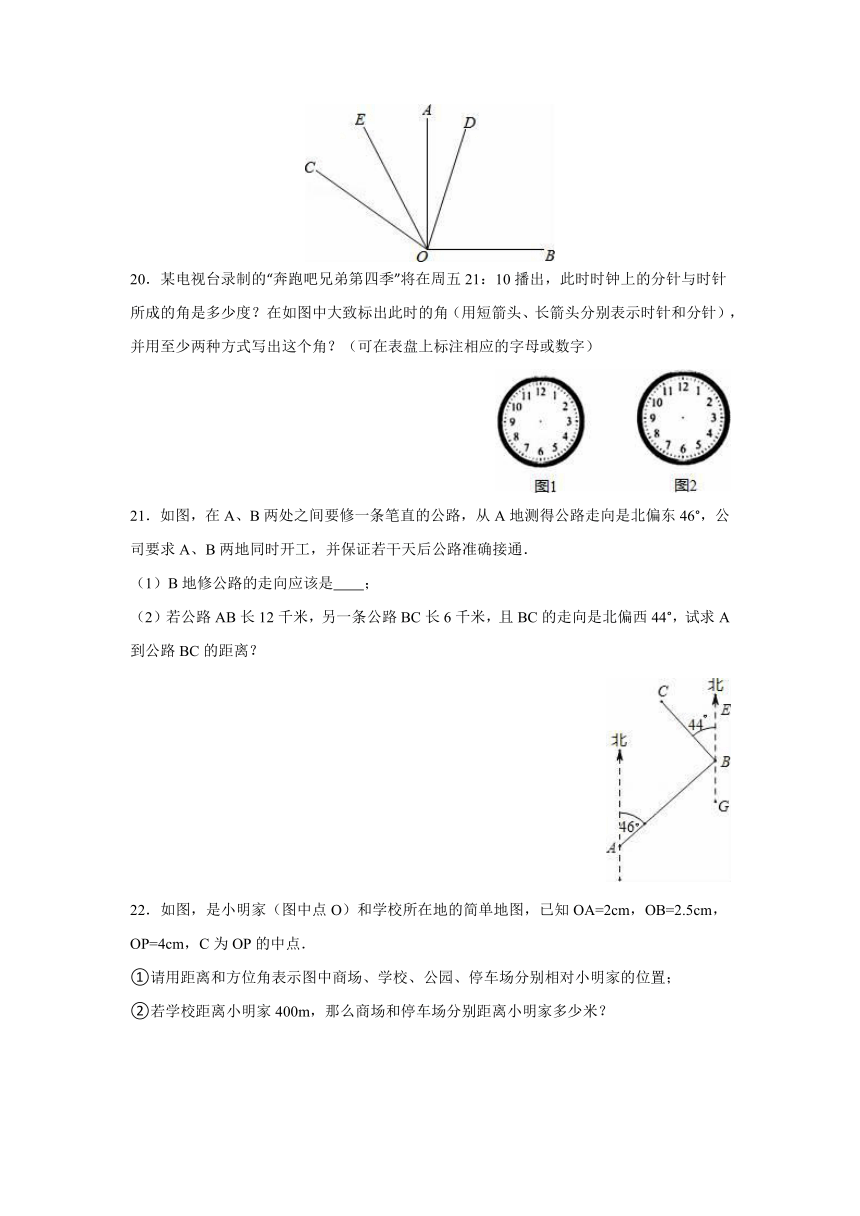
12．如图，点O在直线AB上，射线OC平分∠DOB，若∠COB=35°，则∠AOD=　　°．
13．上午8：30钟表的时针和分针构成角的度数是　　．
14．如图，C岛在A岛的北偏东60°方向，在B岛的北偏西45°方向，则∠ACB=　　．
15．如图所示，一艘船从A点出发，沿东北方向航行至B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于　　度．
16．甲看乙的方向是北偏东40°，那么乙看甲的方向是　　度．
　
三．解答题（共14小题）
17．用两种方法证明“三角形的外角和等于360°”．
如图，∠BAE、∠CBF、∠ACD是△ABC的三个外角．
求证∠BAE+∠CBF+∠ACD=360°．
证法1：∵　　，
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣（∠1+∠2+∠3）．
∵　　，
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°．
请把证法1补充完整，并用不同的方法完成证法2．
18．问题引入：
（1）如图①，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC=　　（用α表示）；如图②，∠CBO=∠ABC，∠BCO=∠ACB，∠A=α，则∠BOC=　　（用α表示）
拓展研究：
（2）如图③，∠CBO=∠DBC，∠BCO=∠ECB，∠A=α，请猜想∠BOC=　　（用α表示），并说明理由．
类比研究：
（3）BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO=∠DBC，∠BCO=∠ECB，∠A=α，请猜想∠BOC=　　．
19．如图，已知同一平面内∠AOB=90°，∠AOC=60°，
（1）填空∠BOC=　　；
（2）如OD平分∠BOC，OE平分∠AOC，直接写出∠DOE的度数为　　°；
（3）试问在（2）的条件下，如果将题目中∠AOC=60°改成∠AOC=2α（α＜45°），其他条件不变，你能求出∠DOE的度数吗？若能，请你写出求解过程；若不能，请说明理由．
20．某电视台录制的“奔跑吧兄弟第四季”将在周五21：10播出，此时时钟上的分针与时针所成的角是多少度？在如图中大致标出此时的角（用短箭头、长箭头分别表示时针和分针），并用至少两种方式写出这个角？（可在表盘上标注相应的字母或数字）
21．如图，在A、B两处之间要修一条笔直的公路，从A地测得公路走向是北偏东46°，公司要求A、B两地同时开工，并保证若干天后公路准确接通．
（1）B地修公路的走向应该是　　；
（2）若公路AB长12千米，另一条公路BC长6千米，且BC的走向是北偏西44°，试求A到公路BC的距离？
22．如图，是小明家（图中点O）和学校所在地的简单地图，已知OA=2cm，OB=2.5cm，OP=4cm，C为OP的中点．
①请用距离和方位角表示图中商场、学校、公园、停车场分别相对小明家的位置；
②若学校距离小明家400m，那么商场和停车场分别距离小明家多少米？
23．如图，点O是直线FA上一点，OB，OD，OC，OE是射线，OE平分∠AOC，OD平分∠BOC．
（1）若∠AOE=15°，求∠FOC的度数；
（2）若∠AOB=86°，求∠DOE的度数．
24．如图，点O为直线AB上一点，过点O作直线OC，已知∠AOC≠90°，射线OD平分∠AOC，射线OE平分∠BOC，射线OF平分∠DOE．求：
（1）当0°＜∠AOC＜90°时，求∠FOB+∠DOC的度数；
（2）若∠DOC=3∠COF，求∠AOC的度数．
25．（1）在图1中，以点P为顶点画∠P，使∠P的两边分别与∠1的两边垂直，则∠P和∠1之间的存在的数量关系是　　；
（2）在图2和图3中，作同样的∠P，则两图中∠P和∠1的数量关系是　　，理由是　　；
（3）由上述三种情形可以得到一个结论：如果一个角的两边分别和另一个角的两边垂直，那么这两个角　　（只需写出结论即可）．
（4）如果一个角的两边分别垂直于另一个角的两边且这两个角的差为40°，那么这两个角的度数分别是　　．
26．（1）在∠AOB内部画1条射线OC，则图1中有　　个不同的角；
（2）在∠AOB内部画2条射线OC，OD，则图2中有　　个不同的角；
（3）在∠AOB内部画3条射线OC，OD，OE，则图3中有　　个不同的角；
（4）在∠AOB内部画10条射线OC，OD，OE…，则图中有　　个不同的角；
（5）在∠AOB内部画n条射线OC，OD，OE…，则图中有　　个不同的角．
27．如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上，同时，在它北偏东30°、西北（即北偏西45°）方向上又分别发现了客轮B和海岛C．
（1）仿照表示灯塔方位的方法，分别画出表示客轮B和海岛C方向的射线OB，OC（不写作法）；
（2）若图中有一艘渔船D，且∠AOD的补角是它的余角的3倍，画出表示渔船D方向的射线OD，则渔船D在货轮O的　　（写出方位角）
28．生活经验：因为你在北半球，用走时准确的手表可以帮你辨别方向．将时针指向太阳所在方向，画它与12点夹角的平分线，这条平分线所指的方向就是南方，如图．
题目：沙漠探险队员用手表定好方位，∠COB=48°，发现一处水源D在7点指的方向，如图．营地E在水源D的北偏东40°方向．
（1）水源D在探险队员的　　偏　　度的方向（方位角）；
（2）在图中画出营地E所在的方向；
（3）求∠EDO的度数．
29．把一副三角板的直角顶点O重叠在一起．
（1）如图（1），当OB平分∠COD时，则∠AOD和∠BOC的和是多少度？
（2）如图（2），当OB不平分∠COD时，则∠AOD和∠BOC的和是多少度？
30．（1）如图1所示，已知∠AOB=120°，OC平分∠AOB，OD、OE分别平分∠AOC、∠COB，求∠DOE的度数；
（2）如图2，在（1）中把“OC平分∠AOB”改为“OC是∠AOB内任意一条射线”，其他任何条件都不变，试求∠DOE的度数；
（3）如图3，在（1）中把“OC平分∠AOB”改为“OC是∠AOB外的一条射线且点C与点B在直线AO的同侧”，其他任何条件都不变，请你直接写出∠DOE的度数．
　
答案与解析
一．选择题
1．（2016 北京）如图所示，用量角器度量∠AOB，可以读出∠AOB的度数为（　　）
A．45°
B．55°
C．125°
D．135°
【分析】由图形可直接得出．
【解答】解：由图形所示，∠AOB的度数为55°，
故选B．
【点评】本题主要考查了角的度量，量角器的使用方法，正确使用量角器是解题的关键．
　
2．（2016 百色）下列关系式正确的是（　　）
A．35.5°=35°5′
B．35.5°=35°50′
C．35.5°＜35°5′
D．35.5°＞35°5′
【分析】根据大单位化小单位乘以进率，可得答案．
【解答】解：A、35.5°=35°30′，35°30′＞35°5′，故A错误；
B、35.5°=35°30′，35°30′＜35°50′，故B错误；
C、35.5°=35°30′，35°30′＞35°5′，故C错误；
D、35.5°=35°30′，35°30′＞35°5′，故D正确；
故选：D．
【点评】本题考查了度分秒的换算，大单位化成效单位乘以进率是解题关键．
　
3．（2016 烟台）如图，Rt△ABC的斜边AB与量角器的直径恰好重合，B点与0刻度线的一端重合，∠ABC=40°，射线CD绕点C转动，与量角器外沿交于点D，若射线CD将△ABC分割出以BC为边的等腰三角形，则点D在量角器上对应的度数是（　　）
A．40°
B．70°
C．70°或80°
D．80°或140°
【分析】如图，点O是AB中点，连接DO，易知点D在量角器上对应的度数=∠DOB=2∠BCD，只要求出∠BCD的度数即可解决问题．
【解答】解：如图，点O是AB中点，连接DO．
∵点D在量角器上对应的度数=∠DOB=2∠BCD，
∵当射线CD将△ABC分割出以BC为边的等腰三角形时，
∠BCD=40°或70°，
∴点D在量角器上对应的度数=∠DOB=2∠BCD=80°或140°，
故选D．
【点评】本题考查圆心角与圆周角的关系，量角器、等腰三角形的判定和性质等知识，解题的关键是理解∠BOD=2∠BCD，学会分类讨论的思想，属于中考常考题型．
　
4．（2016 恩施州）已知∠AOB=70°，以O为端点作射线OC，使∠AOC=42°，则∠BOC的度数为（　　）
A．28°
B．112°
C．28°或112°
D．68°
【分析】根据题意画出图形，利用数形结合求解即可．
【解答】解：如图，当点C与点C1重合时，∠BOC=∠AOB﹣∠AOC=70°﹣42°=28°；
当点C与点C2重合时，∠BOC=∠AOB+∠AOC=70°+42°=112°．
故选C．
【点评】本题考查的是角的计算，在解答此题时要注意进行分类讨论，不要漏解．
　
5．如果从甲船看乙船，乙船在甲船的北偏东30°方向，那么从乙船看甲船，甲船在乙船的（　　）
A．南偏西30°方向
B．南偏西60°方向
C．南偏东30°方向
D．南偏东60°方向
【分析】根据题意正确画出图形进而分析得出从乙船看甲船的方向．
【解答】解：如图所示：可得∠1=30°，
∵从甲船看乙船，乙船在甲船的北偏东30°方向，
∴从乙船看甲船，甲船在乙船的南偏西30°方向．
故选：A．
【点评】此题主要考查了方向角，根据题意画出图形是解题关键．
　
6．如图，在A、B
两地之间要修一条笔直的公路，从A地测得公路走向是北偏东48°，A，B两地同时开工，若干天后公路准确接通，若公路AB长8千米，另一条公路BC长是6千米，且BC的走向是北偏西42°，则A地到公路BC的距离是（　　）
A．6千米
B．8千米
C．10千米
D．14千米
【分析】根据方位角的概念，图中给出的信息，再根据已知转向的角度求解．
【解答】解：根据两直线平行，内错角相等，可得∠ABG=48°，
∵∠ABC=180°﹣∠ABG﹣∠EBC=180°﹣48°﹣42°=90°，
∴AB⊥BC，
∴A地到公路BC的距离是AB=8千米，
故选：B．
【点评】此题是一道方向角问题，结合生活中的实际问题，将解三角形的相关知识有机结合，体现了数学应用于实际生活的思想．
　
7．一艘海上搜救船借助雷达探测仪寻找到事故船的位置，雷达示意图如图所示，搜救船位于图中圆心O处，事故船位于距O点40海里的A处，雷达操作员要用方位角把事故船相对于搜救船的位置汇报给船长，以便调整航向，下列四种表述方式中正确的为（　　）
A．事故船在搜救船的北偏东60°方向
B．事故船在搜救船的北偏东30°方向
C．事故船在搜救船的北偏西60°方向
D．事故船在搜救船的南偏东30°方向
【分析】根据点的位置确定应该有方向以及距离，进而利用图象得出即可．
【解答】解：如图所示：事故船A在搜救船北偏东30°方向，
故选：B．
【点评】此题主要考查了点的坐标确定位置，注意方向角的确定方法．
　
8．如图，在一次定向越野活动中，“超越”小组准备从目前所在的A
处前往相距2km的B处，则相对于A处来说，B处的位置是（　　）
A．南偏西50°，2km
B．南偏东50°，2km
C．北偏西40°，2km
D．北偏东40°，2km
【分析】直接利用方向角的定义得出相对于A处来说，B处的位置．
【解答】解：如图所示：相对于A处来说，B处的位置是：南偏西50°，2km．
故选：A．
【点评】此题主要考查了方向角，利用方向角确定位置是解题关键．
　
二．填空题（共8小题）
9．（2016 雅安）1.45°=　87′　．
【分析】直接利用度分秒的转化将0.45°转会为分即可．
【解答】解：1.45°=60′+0.45×60′=87′．
故答案为：87′．
【点评】此题主要考查了度分秒的转化，正确掌握度分秒之间的关系是解题关键．
　
10．北偏东30°与南偏东50°的两条射线组成的角的度数为　100　°．
【分析】根据方向角的表示方法，可得答案．
【解答】解：如图：
北偏东30°与南偏东50°的两条射线组成的角的度数为180﹣30﹣50=100°，
故答案为：100．
【点评】本题考查了方向角，画出图形，利用数形结合是解题关键．
　
11．计算33°52′+21°54′=　55°46′　．
【分析】相同单位相加，分满60，向前进1即可．
【解答】解：33°52′+21°54′=54°106′=55°46′．
【点评】计算方法为：度与度，分与分对应相加，分的结果若满60，则转化为1度．
12．如图，点O在直线AB上，射线OC平分∠DOB，若∠COB=35°，则∠AOD=　110　°．
【分析】首先根据角平分线定义可得∠BOD=2∠BOC=70°，再根据邻补角的性质可得∠AOD的度数．
【解答】解：∵射线OC平分∠DOB．
∴∠BOD=2∠BOC，
∵∠COB=35°，
∴∠DOB=70°，
∴∠AOD=180°﹣70°=110°，
故答案是：110．
【点评】此题主要考查了角平分线定义，关键是掌握角平分线把角分成相等的两部分．
　
13．上午8：30钟表的时针和分针构成角的度数是　75°　．
【分析】本题考查了钟表里的旋转角的问题，钟表表盘被分成12大格，每一大格又被分为5小格，故表盘共被分成60小格，每一小格所对角的度数为6°．分针转动一圈，时间为60分钟，则时针转1大格，即时针转动30°．也就是说，分针转动360°时，时针才转动30°，即分针每转动1°，时针才转动（）度，逆过来同理．
【解答】解：∵8时30分时，时针指向8与9之间，分针指向6．钟表12个数字，每相邻两个数字之间的夹角为30°，
∴8时30分时分针与时针的夹角是2×30°+15°=75°．
故答案为：75°．
【点评】本题考查的是钟表表盘与角度相关的特征．能更好地认识角，感受角的大小．
　
14．如图，C岛在A岛的北偏东60°方向，在B岛的北偏西45°方向，则∠ACB=　105°　．
【分析】过点C作CD∥AE，从而可证明CD∥BF，然后由平行线的性质可知∠DCA=∠CAE，∠DCB=∠CBF，从而可求得∠ACB的度数．
【解答】解：过点C作CD∥AE．
∵CD∥AE，BF∥AE，
∴CD∥BF．
∵CD∥AE，
∴∠DCA=∠CAE=60°，
同理：∠DCB=∠CBF=45°．
∴∠ACB=∠ACD+∠BCD=105°．
【点评】本题主要考查的是方向角的定义和平行线的性质的应用，掌握此类问题辅助线的作法是解题的关键．
　
15．如图所示，一艘船从A点出发，沿东北方向航行至B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于　60　度．
【分析】根据南北方向是平行的得出∠ABF=45°，再和∠CBF相加即可得出答案．
【解答】解：
∵AE∥BF，
∴∠ABF= EAB=45°，
∴∠ABC=∠ABF+∠CBF=45°+15°=60°，
故答案为：60．
【点评】本题考查了方向角和角的有关计算的应用，主要考查学生的计算能力．
　
16．甲看乙的方向是北偏东40°，那么乙看甲的方向是　南偏西40°　度．
【分析】甲看乙的方向是北偏东40°，是以甲为标准，反之乙看甲的方向是甲相对于乙的方向与位置．方向完全相反，角度不变．
【解答】解：甲看乙的方向是北偏东40°，则乙看甲的方向是南偏西40°，
故答案为：南偏西40°．
【点评】本题考查了方向角的定义，理解定义是关键．
　
三．解答题（共14小题）
17．（2016 南京）用两种方法证明“三角形的外角和等于360°”．
如图，∠BAE、∠CBF、∠ACD是△ABC的三个外角．
求证∠BAE+∠CBF+∠ACD=360°．
证法1：∵　平角等于180°　，
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣（∠1+∠2+∠3）．
∵　∠1+∠2+∠3=180°　，
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°．
请把证法1补充完整，并用不同的方法完成证法2．
【分析】证法1：根据平角的定义得到∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=540°，再根据三角形内角和定理和角的和差关系即可得到结论；
证法2：要求证∠BAE+∠CBF+∠ACD=360°，根据三角形外角性质得到∠BAE=∠2+∠3，∠CBF=∠1+∠3，∠ACD=∠1+∠2，则∠BAE+∠CBF+∠ACD=2（∠1+∠2+∠3），然后根据三角形内角和定理即可得到结论．
【解答】证明：证法1：∵平角等于180°，
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°，
∴∠BAE+∠CBF+∠ACD=540°﹣（∠1+∠2+∠3）．
∵∠1+∠2+∠3=180°，
∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°．
证法2：∵∠BAE=∠2+∠3，∠CBF=∠1+∠3，∠ACD=∠1+∠2，
∴∠BAE+∠CBF+∠ACD=2（∠1+∠2+∠3），
∵∠1+∠2+∠3=180°，
∴∠BAE+∠CBF+∠ACD=360°．
故答案为：平角等于180°，∠1+∠2+∠3=180°．
【点评】本题考查了多边形的外角和：n边形的外角和为360°．也考查了三角形内角和定理和外角性质．
　
18．（2016 内江）问题引入：
（1）如图①，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC=　90°+α　（用α表示）；如图②，∠CBO=∠ABC，∠BCO=∠ACB，∠A=α，则∠BOC=　120°+α　（用α表示）
拓展研究：
（2）如图③，∠CBO=∠DBC，∠BCO=∠ECB，∠A=α，请猜想∠BOC=　120°﹣α　（用α表示），并说明理由．
类比研究：
（3）BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO=∠DBC，∠BCO=∠ECB，∠A=α，请猜想∠BOC=　﹣α　．
【分析】（1）如图①，根据角平分线的定义可得∠OBC=∠ABC，∠OCB=∠ACB，然后表示出∠OBC+∠OCB，再根据三角形的内角和等于180°列式整理即可得∠BOC=90°+α；如图②，根据三角形的内角和等于180°列式整理即可得∠BOC=120°+α；
（2）如图③，根据三角形的内角和等于180°列式整理即可得∠BOC=120°﹣α；
（3）根据三角形的内角和等于180°列式整理即可得∠BOC=﹣α．
【解答】解：（1）如图①，∵∠ABC与∠ACB的平分线相交于点O，
∴∠OBC=∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=（∠ABC+∠ACB），
在△OBC中，∠BOC=180°﹣（∠OBC+∠OCB）
=180°﹣（∠ABC+∠ACB）
=180°﹣（180°﹣∠A）
=90°+∠A
=90°+α；
如图②，在△OBC中，∠BOC=180°﹣（∠OBC+∠OCB）
=180°﹣（∠ABC+∠ACB）
=180°﹣（180°﹣∠A）
=120°+∠A
=120°+α；
（2）如图③，在△OBC中，∠BOC=180°﹣（∠OBC+∠OCB）
=180°﹣（∠DBC+∠ECB）
=180°﹣（∠A+∠ACB+∠A+ABC）
=180°﹣（∠A+180°）
=120°﹣α；
（3）在△OBC中，∠BOC=180°﹣（∠OBC+∠OCB）
=180°﹣（∠DBC+∠ECB）
=180°﹣（∠A+∠ACB+∠A+ABC）
=180°﹣（∠A+180°）
=﹣α．
故答案为90°+α，120°+α；120°﹣α；﹣α．
【点评】本题考查了三角形的内角和定理，角平分线的定义，整体思想的利用是解题的关键．
　
19．如图，已知同一平面内∠AOB=90°，∠AOC=60°，
（1）填空∠BOC=　150°　；
（2）如OD平分∠BOC，OE平分∠AOC，直接写出∠DOE的度数为　45　°；
（3）试问在（2）的条件下，如果将题目中∠AOC=60°改成∠AOC=2α（α＜45°），其他条件不变，你能求出∠DOE的度数吗？若能，请你写出求解过程；若不能，请说明理由．
【分析】（1）直接根据已知利用∠BOC=∠AOB+∠AOC求出即可；
（2）利用角平分线的性质和（1）中所求得出答案即可；
（3）根据角平分线的性质∠DOC=∠BOC=45°+α，∠COE=∠AOC=α，进而求出即可．
【解答】解：（1）∵∠AOB=90°，∠AOC=60°，
∴∠BOC=∠AOB+∠AOC=90°+60°=150°，
故答案为：150°；
（2）∵OD平分∠BOC，OE平分∠AOC，
∴∠COD=∠BOC=75°，∠COE=∠AOC=30°，
∴∠DOE的度数为：∠COD﹣∠COE=45°；
故答案为：45；
（3）∵∠AOB=90°，∠AOC=2α，
∴∠BOC=90°+2α，
∵OD、OE平分∠BOC，∠AOC，
∴∠DOC=∠BOC=45°+α，∠COE=∠AOC=α，
∴∠DOE=∠DOC﹣∠COE=45°．
【点评】此题主要考查了角平分线的性质以及有关角的计算，熟练利用角平分线的性质得出是解题关键．
　
20．某电视台录制的“奔跑吧兄弟第四季”将在周五21：10播出，此时时钟上的分针与时针所成的角是多少度？在如图中大致标出此时的角（用短箭头、长箭头分别表示时针和分针），并用至少两种方式写出这个角？（可在表盘上标注相应的字母或数字）
【分析】直接利用时针每分钟走0.5°，分钟每分钟走6°，进而求出答案．
【解答】解：如图所示：∵时针每分钟走0.5°，
分钟每分钟走6°，
21点时分针与时针的夹角为90°，
∴10×6°=60°，10×0.5°=5°，
21点时夹角为：90°+60°﹣5°=145°．
可以表示为∠1，∠AOB，∠O等．
【点评】此题主要考查了钟面角以及角的表示方法，正确得出时针与分钟转动速度是解题关键．
　
21．如图，在A、B两处之间要修一条笔直的公路，从A地测得公路走向是北偏东46°，公司要求A、B两地同时开工，并保证若干天后公路准确接通．
（1）B地修公路的走向应该是　南偏西46°　；
（2）若公路AB长12千米，另一条公路BC长6千米，且BC的走向是北偏西44°，试求A到公路BC的距离？
【分析】根据方位角的概念，图中给出的信息，再根据已知转向的角度求解．
【解答】解：（1）由两地南北方向平行，根据内错角相等，可知B地所修公路的走向是南偏西46°．
（2）∵∠ABC=180°﹣∠ABG﹣∠EBC=180°﹣46°﹣44°=90°，
∴AB⊥BC，
∴A地到公路BC的距离是AB=12千米．
故答案为：南偏西46°．
【点评】此题考查了方向角问题，结合生活中的实际问题，将解三角形的相关知识有机结合，体现了数学应用于实际生活的思想．
　
22．如图，是小明家（图中点O）和学校所在地的简单地图，已知OA=2cm，OB=2.5cm，OP=4cm，C为OP的中点．
①请用距离和方位角表示图中商场、学校、公园、停车场分别相对小明家的位置；
②若学校距离小明家400m，那么商场和停车场分别距离小明家多少米？
【分析】①根据方位角定义及图中线段的长度即可得知；
②根据学校距离小明家400m而图中对应线段OA=2cm可知图中1cm表示200m，再根据OB、OP的长即可得．
【解答】解：①商场在小明家西偏北60°方向，距离2.5cm位置，
学校在小明家东偏北45°方向，距离2cm位置，
公园在小明家东偏南30°方向，距离2cm位置，
停车场在小明家东偏南30°方向，距离4cm位置；
②∵学校距离小明家400m，且OA=2cm，
∴图中1cm表示200m，
∴商场距离小明家2.5×200=500m，
停车场距离小明家4×200=800m．
【点评】本题主要考查方向角的概念，用方位角描述方向时，通常以正北或正南方向为角的始边，以对象所处的射线为终边，故描述方位角时，一般先叙述北或南，再叙述偏东或偏西．
　
23．如图，点O是直线FA上一点，OB，OD，OC，OE是射线，OE平分∠AOC，OD平分∠BOC．
（1）若∠AOE=15°，求∠FOC的度数；
（2）若∠AOB=86°，求∠DOE的度数．
【分析】（1）先根据角平分线，求得∠AOC的度数，再根据邻补角求得∠FOC的度数；
（2）先根据角平分线得到∠EOC=∠AOC，∠DOC=∠BOC，再根据角的和差关系进行计算即可．
【解答】解：（1）∵∠AOE=15°，OE平分∠AOC，
∴∠AOC=2×15°=30°，
∵点O是直线FA上一点，
∴∠FOC=180°﹣30°=150°；
（2）∵OE平分∠AOC，OD平分∠BOC，
∴∠EOC=∠AOC，∠DOC=∠BOC，
∴∠DOE=∠AOC+∠BOC=∠AOB=×86°=43°．
【点评】本题主要考查了角平分线的定义，根据角平分线定义得出所求角与已知角的关系是解决问题的关键．
　
24．如图，点O为直线AB上一点，过点O作直线OC，已知∠AOC≠90°，射线OD平分∠AOC，射线OE平分∠BOC，射线OF平分∠DOE．求：
（1）当0°＜∠AOC＜90°时，求∠FOB+∠DOC的度数；
（2）若∠DOC=3∠COF，求∠AOC的度数．
【分析】（1）先根据射线OD平分∠AOC，∠AOD=∠COD，射线OE平分∠BOC，得∠COE=∠BOE，再根据∠AOC+∠BOC=180°，得出∠DOE=90°，由射线OF平分∠DOE，得∠DOF=∠EOF=45°，从而求得∠FOB+∠DOC的度数；
（2）设∠AOD=∠COD=x°，分∠AOC为锐角和钝角两种情况，根据∠DOC=3∠COF，得出x的值，即可求得∠AOC的度数．
【解答】解：如图1，
（1）∵射线OD平分∠AOC，
∴∠AOD=∠COD，
∵射线OE平分∠BOC，
∴∠COE=∠BOE，
∵∠AOC+∠BOC=180°，
∴∠DOE=∠DOC+∠EOC=∠AOC+∠BOC=90°，
∵OF平分∠DOE，
∴∠DOF=∠EOF=∠DOE=45°，
∴∠FOB+∠DOC=∠BOF+∠AOD=180°﹣∠DOF=180°﹣45°=135°；
（2）设∠AOD=∠COD=x°，则∠AOC=2x°，
由（1）的证明过程可知∠DOE=90°，∠DOF=∠EOF=45°，
∠AOC≠90°，分情况考虑如下：
①当∠AOC为锐角时，如图1，∠COF=∠DOF﹣∠COD=45°﹣x，
∵∠DOC=3∠COF，
∴x=3 （45°﹣x），
解得x=33.75°，
∴∠AOC=2x=67.5°．
②当∠AOC为钝角时，如图2，∠COF=∠COD﹣∠DOF=x﹣45°，
∵∠DOC=3∠COF，
∴x=3 （x﹣45°），
解得x=67.5°，
∴∠AOC=2x=135°．
综合，可得∠AOC=67.5°或135°．
【点评】本题考查了角的计算和角平分线的定义，一定要注意角平分线的几种表示方法．如：∠1=∠2，∠1=∠AOB，∠AOB=2∠1．
　
25．（1）在图1中，以点P为顶点画∠P，使∠P的两边分别与∠1的两边垂直，则∠P和∠1之间的存在的数量关系是　互补　；
（2）在图2和图3中，作同样的∠P，则两图中∠P和∠1的数量关系是　相等　，理由是　同角（或等角）的余角相等　；
（3）由上述三种情形可以得到一个结论：如果一个角的两边分别和另一个角的两边垂直，那么这两个角　相等或互补　（只需写出结论即可）．
（4）如果一个角的两边分别垂直于另一个角的两边且这两个角的差为40°，那么这两个角的度数分别是　110°和70°　．
【分析】（1）根据四边形内角和定理即可判断．
（2）根据同角（或等角）的余角相等，即可判断．
（3）由（1）（2）可知结论．
（4）理由（3）中结论即可解决问题．
【解答】解：（1）∠P与∠1互补．
故答案为互补．
（2）∠P=∠1相等．理由：同角（或等角）的余角相等．
故答案为相等，同角（或等角）的余角相等．
（3）相等或互补．
故答案为相等或互补．
（4）由题意这两个角互补，不妨设这两个角分别为α、β．（α＞β）
则
解得
故答案为110°和70°．
【点评】本题考查角的计算，互余、互补等知识，解题的关键是学会正确画好图形，学会利用结论解决问题，属于中考常考题型．
　
26．（1）在∠AOB内部画1条射线OC，则图1中有　3　个不同的角；
（2）在∠AOB内部画2条射线OC，OD，则图2中有　6　个不同的角；
（3）在∠AOB内部画3条射线OC，OD，OE，则图3中有　10　个不同的角；
（4）在∠AOB内部画10条射线OC，OD，OE…，则图中有　66　个不同的角；
（5）在∠AOB内部画n条射线OC，OD，OE…，则图中有　　个不同的角．
【分析】（1）根据图形数出即可；
（2）根据图形数出即可；
（3）根据图形数出即可；
（4）有1+2+3+…+9+10+11=66个角；
（5）求出1+2+3+…+n+（n+1）的值即可．
【解答】解：（1）在∠AOB内部画1条射线OC，则图中有3个不同的角，
故答案为：3．
（2）在∠AOB内部画2条射线OC，OD，则图中有6个不同的角，
故答案为：6．
（3）在∠AOB内部画3条射线OC，OD，OE，则图中有10个不同的角，
故答案为：10．
（4）在∠AOB内部画10条射线OC，OD，OE，…，则图中有1+2+3+…+10+11=66个不同的角，
故答案为：66．
（5）在∠AOB内部画n条射线OC，OD，OE，…，则图中有1+2+3+…+n+（n+1）=个不同的角．
故答案为：．
【点评】本题考查了角的有关概念的应用，关键是能根据题意得出规律．
　
27．如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上，同时，在它北偏东30°、西北（即北偏西45°）方向上又分别发现了客轮B和海岛C．
（1）仿照表示灯塔方位的方法，分别画出表示客轮B和海岛C方向的射线OB，OC（不写作法）；
（2）若图中有一艘渔船D，且∠AOD的补角是它的余角的3倍，画出表示渔船D方向的射线OD，则渔船D在货轮O的　D在O南偏东15°或北偏东75°　（写出方位角）
【分析】（1）根据方向角的度数，可得答案；
（2）根据余角与补角的关系，可得∠AOD的度数，根据角的和差，可得方向角．
【解答】解：（1）如图1：
，
（2）如图2：
，
由∠AOD的补角是它的余角的3倍，得
180°﹣∠AOD=3（180°﹣∠AOD）．
解得∠AOD=45°．
故D在O南偏东15°或北偏东75°．
故答案为：D在O南偏东15°或北偏东75°．
【点评】本题考查了方向角，利用余角与补角的关系得出∠AOD的度数是解题关键．
　
28．生活经验：因为你在北半球，用走时准确的手表可以帮你辨别方向．将时针指向太阳所在方向，画它与12点夹角的平分线，这条平分线所指的方向就是南方，如图．
题目：沙漠探险队员用手表定好方位，∠COB=48°，发现一处水源D在7点指的方向，如图．营地E在水源D的北偏东40°方向．
（1）水源D在探险队员的　西　偏　北72　度的方向（方位角）；
（2）在图中画出营地E所在的方向；
（3）求∠EDO的度数．
【分析】（1）过O作直线OF⊥OC，则OF为北，求出∠DOF=72°，则水源D在探险队员的西偏北72°的方向；
（2）过点D画出四个方位，标出营地E所在的方向；
（3）先求∠ODF=90°﹣72°=18°，再根据平角定义求出结论．
【解答】解：（1）过O作直线OF⊥OC，
则∠FOB=90°﹣48°=42°，
∵OC平分∠AOB，
∴∠AOB=2∠BOC=96°，
∴∠DOB=180°﹣96°+30°=114°，
∴∠DOF=114°﹣42°=72°，
则水源D在探险队员的西偏北72°的方向，
故答案为：西，北72；
（2）如图所示，
（3）在Rt△DOF中，∠ODF=90°﹣72°=18°，
∴∠EDO=180°﹣40°﹣18°=122°．
【点评】本题考查了方位角问题，这是数学中的一个难点，本题需要理解方位角的概念；解答此类题需要从运动的角度，正确画出四个方位：东、南、西、北，再结合三角形的内角和及角平分线和平角的关系求解．
　
29．把一副三角板的直角顶点O重叠在一起．
（1）如图（1），当OB平分∠COD时，则∠AOD和∠BOC的和是多少度？
（2）如图（2），当OB不平分∠COD时，则∠AOD和∠BOC的和是多少度？
【分析】已知一副三角板的直角顶点O重叠在一起，就是已知图形中的两个三角形各角的度数，这样重叠时存在的角的关系是：∠AOD=∠AOB+∠COD﹣∠COB．
【解答】解：（1）∵OB平分∠COD，
∴∠COB=∠BOD=45°，
∴∠COA=90°﹣45°=45°，
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC
=45°+90°+45°=180°，
∴∠AOD和∠BOC的和是180°．
（2）∵∠AOC+∠BOC=90°，∠BOD+∠BOC=90°，
∴∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC
∴∠AOD+∠BOC=（∠AOC+∠BOC）+（∠BOD+∠BOC）
=90°+90°=180°．
∴∠AOD和∠BOC的和是180°．
【点评】根据角平分线定义得出所求角与已知角的关系转化求解．注意一副三角板的直角顶点O重叠在一起时角的关系．
　
30．（1）如图1所示，已知∠AOB=120°，OC平分∠AOB，OD、OE分别平分∠AOC、∠COB，求∠DOE的度数；
（2）如图2，在（1）中把“OC平分∠AOB”改为“OC是∠AOB内任意一条射线”，其他任何条件都不变，试求∠DOE的度数；
（3）如图3，在（1）中把“OC平分∠AOB”改为“OC是∠AOB外的一条射线且点C与点B在直线AO的同侧”，其他任何条件都不变，请你直接写出∠DOE的度数．
【分析】（1）根据角平分线定义求出∠BOC和∠AOC度数，即可得出答案；
（2）根据角平分线定义得出∠COD=∠AOC，∠COE=∠BOC，求出∠DOE=∠COD+∠COE=∠AOB，代入求出即可；
（3）根据角平分线定义得出∠COD=∠AOC，∠COE=∠BOC，求出∠DOE=∠COD﹣∠COE=∠AOB，代入求出即可．
【解答】解：（1）∵∠AOB=120°，0C平分∠AOB，
∴∠AOC=∠COB=∠AOB=60°，
∵OD、OE分别平分∠AOC、∠COB，
∴∠COD=∠AOC=30°，∠COE=∠BOC=30°，
∴∠DOE=∠COD+∠COE=30°+30°=60°；
（2）∵OD、OE分别平分∠AOC、∠COB，
∴∠COD=∠AOC，∠COE=∠BOC，
∴∠DOE=∠COD+∠COE=（∠AOC+∠BOC）=∠AOB=×120°=60°；
（3）∵OD、OE分别平分∠AOC、∠COB