14.2.4其他判定两个三角形全等的条件【课件】
文档属性
| 名称 | 14.2.4其他判定两个三角形全等的条件【课件】 |

|
|
| 格式 | zip | ||
| 文件大小 | 393.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 00:00:00 | ||
图片预览




文档简介
课件13张PPT。4.其他判定两个三角形全等的条件教学目标1、了解AAS的适用条件
2、会用AAS证明三角形全等预学检测1、本节课主要学习那些内容?
2、你认为本节课的重点内容是什么?
3、你对哪些内容有疑问?
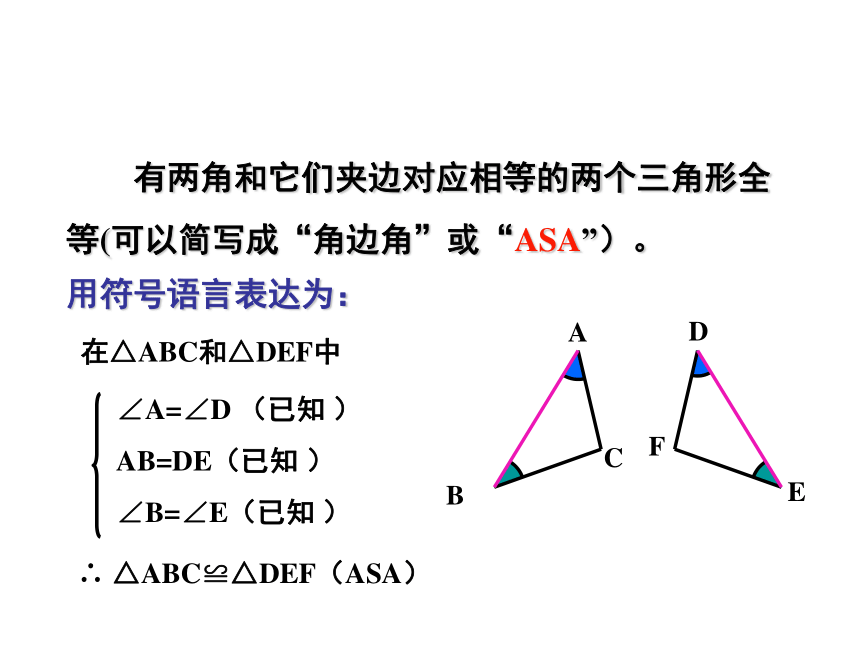
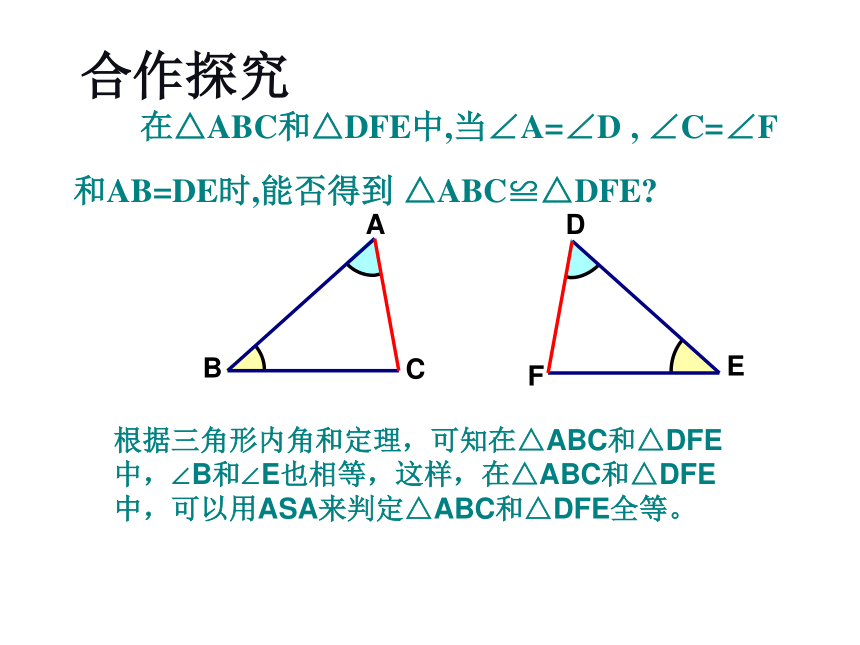
在△ABC和△DEF中∴ △ABC≌△DEF(ASA) 有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。用符号语言表达为:FEDCBA 在△ABC和△DFE中,当∠A=∠D , ∠C=∠F和AB=DE时,能否得到 △ABC≌△DFE?合作探究根据三角形内角和定理,可知在△ABC和△DFE中,∠B和∠E也相等,这样,在△ABC和△DFE中,可以用ASA来判定△ABC和△DFE全等。定理两角分别相等且其中一组等角的对边相等的两个三角形全等。简记为“角角边”或.AAS1.两个直角三角形中,斜边和一锐角对应相等,这两个
直角三角形全等吗?为什么?2.两个直角三角形中,有一条直角边和一锐角对应相
等,这两个直角三角形全等吗?为什么?答:全等,根据AAS答:全等,根据AAS 例1:如图,点D在AB上,点E在AC上,AB=AC, ∠B= ∠C,求证:AD=AE ∠B=∠C(已知) 证明:在△ABE和△ACD中AB=AC(已知)∠A=∠A(公共角)∴△ABE≌△ACD(ASA)∴AD=AE(全等三角形的对应边相等) 已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD
在△ABD和△ABC中
∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
证明:ABCDE12 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?解: △ABC和△ADE全等。
∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC ∴ △ABC≌△ADE(AAS)在△ABC和△ADC 中即∠BAC=∠DAE =(已知)ADAB(1) 两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.(2)三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。总结提升 布置作业 课堂作业:P107练习第二题
家庭作业:1、
2、预学下一节内容。 教学反思
2、会用AAS证明三角形全等预学检测1、本节课主要学习那些内容?
2、你认为本节课的重点内容是什么?
3、你对哪些内容有疑问?
在△ABC和△DEF中∴ △ABC≌△DEF(ASA) 有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。用符号语言表达为:FEDCBA 在△ABC和△DFE中,当∠A=∠D , ∠C=∠F和AB=DE时,能否得到 △ABC≌△DFE?合作探究根据三角形内角和定理,可知在△ABC和△DFE中,∠B和∠E也相等,这样,在△ABC和△DFE中,可以用ASA来判定△ABC和△DFE全等。定理两角分别相等且其中一组等角的对边相等的两个三角形全等。简记为“角角边”或.AAS1.两个直角三角形中,斜边和一锐角对应相等,这两个
直角三角形全等吗?为什么?2.两个直角三角形中,有一条直角边和一锐角对应相
等,这两个直角三角形全等吗?为什么?答:全等,根据AAS答:全等,根据AAS 例1:如图,点D在AB上,点E在AC上,AB=AC, ∠B= ∠C,求证:AD=AE ∠B=∠C(已知) 证明:在△ABE和△ACD中AB=AC(已知)∠A=∠A(公共角)∴△ABE≌△ACD(ASA)∴AD=AE(全等三角形的对应边相等) 已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD
在△ABD和△ABC中
∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (AAS)
∴AC=AD (全等三角形对应边相等)
证明:ABCDE12 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?解: △ABC和△ADE全等。
∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC ∴ △ABC≌△ADE(AAS)在△ABC和△ADC 中即∠BAC=∠DAE =(已知)ADAB(1) 两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.(2)三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。总结提升 布置作业 课堂作业:P107练习第二题
家庭作业:1、
2、预学下一节内容。 教学反思
