14.2.4.其他判定两个三角形全等的条件【导学案 无答案】
文档属性
| 名称 | 14.2.4.其他判定两个三角形全等的条件【导学案 无答案】 |
|
|
| 格式 | zip | ||
| 文件大小 | 153.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
4.其他判定两个三角形全等的条件
学习目标:
1、掌握好AAS定理的内容及它的三个条件;
2、能通过已知及推证得到必要的三个条件,从而证明两三角形全等;
3、提高利用图形及已知进行推理,得到需要的条件从而证明三角形全等。
(一)、自学导航:
1、判定两个三角形全等我们学过了什么方法?它有几个条件,它们之间有什么限制。
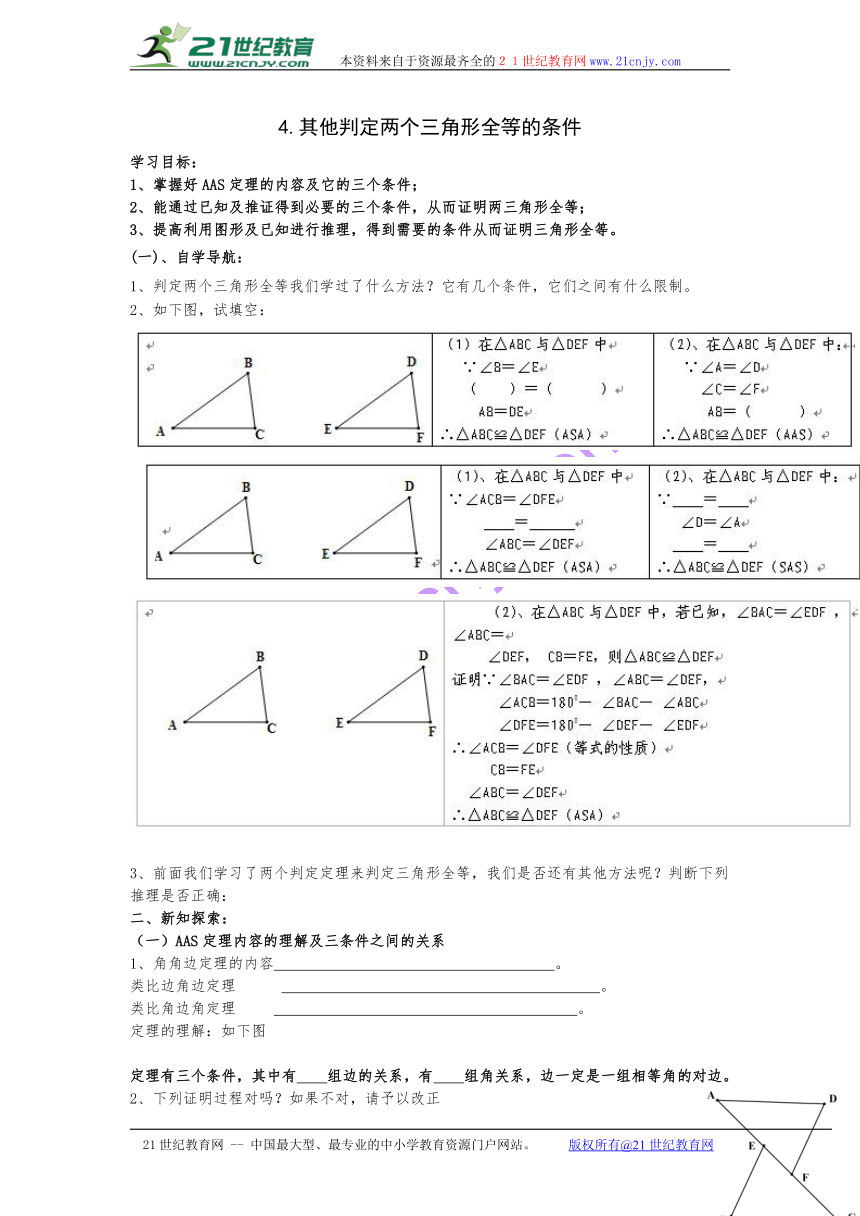
2、如下图,试填空:
3、前面我们学习了两个判定定理来判定三角形全等,我们是否还有其他方法呢?判断下列推理是否正确:
二、新知探索:
(一)AAS定理内容的理解及三条件之间的关系
1、角角边定理的内容
。
类比边角边定理
。
类比角边角定理
。
定理的理解:如下图
定理有三个条件,其中有 组边的关系,有 组角关系,边一定是一组相等角的对边。
2、下列证明过程对吗?如果不对,请予以改正
加深对AAS的理解。记住相等的边关系指的是:对应角(相等的角)的所对的边。
(二)定理的运用:
1、如下图,已知BE∥DF,∠B=∠D,AE=CF,(1)试证明:△ADF≌△CBE;
分析:(1)已知有一组角相等,并有线段相等,我们观察能否得到边相等,
(三种方法都必需有边的相等关系)
给出了平行,我们能联想到角的关系。
(2)看到这种类似滑动的图形,我们就想到等量加等量和相等的运用。
2、已知如图,∠BAD=∠CAD,∠B=∠C,求证:(1)△ADB≌△ADC,(2)AD⊥BC
分析:(1)有两组的条件,缺少一个条件,并且一定是边的条件,你能从图中有所发现吗?
且哪种方法可以证明两三角形全等呢?
讨论完成。
(2)可证明∠ADB=∠ADC=900
3、已知如图,AB∥DE,∠A=∠D,BE=CF,求证:AC=DF
分析:
证
AC=DF,可找到它们所在的三角形,证明三角形全等,
再找三角形中的边与角关系。
特别注意,一定要是三角形的边与角才可以。
(四)拓展运用:
1、已知如左图,△ABC中,AB=CB,∠BEC=∠BDA,AD与CE相交于点F,
(1)试证明:BE=BD;
(2)试证明:AE=CD;
(3)试证明△AFE≌△CFD
(4)试证明:∠FCA=∠FAC,试判断△AFC的形状。
分析:(1)证BE=BD的方法,再找到条件进行推理。
(2)从图中你能看到AB、BE、AE;CB,BD,CD的关系吗?
(3)有AE=CD了,你还能找到其他的有吗?
(四)自我归纳:
1、我们学习了两个判定三角形全等的方法,分别是 、 与 。它们都必需满足三个条件,我们要记牢。21世纪教育网版权所有
2、证明线段及角相等的办法,可以通过证明它们所在的三角形全等来解决。
(六)课堂检测题:
1、已知如图,∠A=∠D,AB=CD,求证:(1)△ABO≌△DCO;(2)BO=CO,AO=DO
2、已知如图,AB∥DE,AC∥DF,且AC=DF,求证:(1)△ABC≌△DEF;(2)BC=EF,BF=CE21教育网
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
4.其他判定两个三角形全等的条件
学习目标:
1、掌握好AAS定理的内容及它的三个条件;
2、能通过已知及推证得到必要的三个条件,从而证明两三角形全等;
3、提高利用图形及已知进行推理,得到需要的条件从而证明三角形全等。
(一)、自学导航:
1、判定两个三角形全等我们学过了什么方法?它有几个条件,它们之间有什么限制。
2、如下图,试填空:
3、前面我们学习了两个判定定理来判定三角形全等,我们是否还有其他方法呢?判断下列推理是否正确:
二、新知探索:
(一)AAS定理内容的理解及三条件之间的关系
1、角角边定理的内容
。
类比边角边定理
。
类比角边角定理
。
定理的理解:如下图
定理有三个条件,其中有 组边的关系,有 组角关系,边一定是一组相等角的对边。
2、下列证明过程对吗?如果不对,请予以改正
加深对AAS的理解。记住相等的边关系指的是:对应角(相等的角)的所对的边。
(二)定理的运用:
1、如下图,已知BE∥DF,∠B=∠D,AE=CF,(1)试证明:△ADF≌△CBE;
分析:(1)已知有一组角相等,并有线段相等,我们观察能否得到边相等,
(三种方法都必需有边的相等关系)
给出了平行,我们能联想到角的关系。
(2)看到这种类似滑动的图形,我们就想到等量加等量和相等的运用。
2、已知如图,∠BAD=∠CAD,∠B=∠C,求证:(1)△ADB≌△ADC,(2)AD⊥BC
分析:(1)有两组的条件,缺少一个条件,并且一定是边的条件,你能从图中有所发现吗?
且哪种方法可以证明两三角形全等呢?
讨论完成。
(2)可证明∠ADB=∠ADC=900
3、已知如图,AB∥DE,∠A=∠D,BE=CF,求证:AC=DF
分析:
证
AC=DF,可找到它们所在的三角形,证明三角形全等,
再找三角形中的边与角关系。
特别注意,一定要是三角形的边与角才可以。
(四)拓展运用:
1、已知如左图,△ABC中,AB=CB,∠BEC=∠BDA,AD与CE相交于点F,
(1)试证明:BE=BD;
(2)试证明:AE=CD;
(3)试证明△AFE≌△CFD
(4)试证明:∠FCA=∠FAC,试判断△AFC的形状。
分析:(1)证BE=BD的方法,再找到条件进行推理。
(2)从图中你能看到AB、BE、AE;CB,BD,CD的关系吗?
(3)有AE=CD了,你还能找到其他的有吗?
(四)自我归纳:
1、我们学习了两个判定三角形全等的方法,分别是 、 与 。它们都必需满足三个条件,我们要记牢。21世纪教育网版权所有
2、证明线段及角相等的办法,可以通过证明它们所在的三角形全等来解决。
(六)课堂检测题:
1、已知如图,∠A=∠D,AB=CD,求证:(1)△ABO≌△DCO;(2)BO=CO,AO=DO
2、已知如图,AB∥DE,AC∥DF,且AC=DF,求证:(1)△ABC≌△DEF;(2)BC=EF,BF=CE21教育网
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
