1.2.1 几个常用函数的导数与基本初等函数的导数公式 课件2
文档属性
| 名称 | 1.2.1 几个常用函数的导数与基本初等函数的导数公式 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 765.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 00:00:00 | ||
图片预览








文档简介
课件24张PPT。1.2.1 几个常用函数的导数
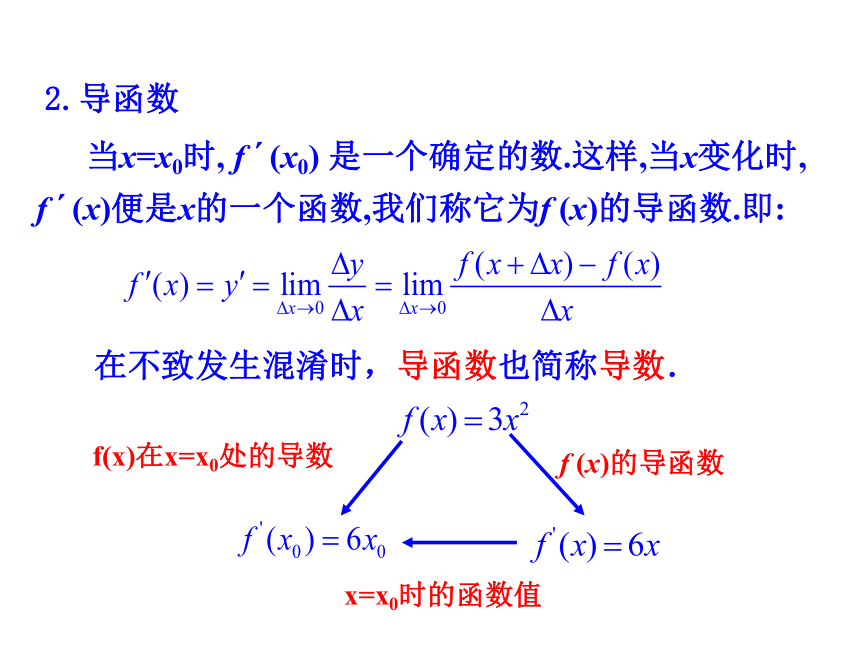
与基本初等函数的导数公式 1.求函数在点x0处的导数的方法是:在不致发生混淆时,导函数也简称导数.2.导函数 当x=x0时, f ′(x0) 是一个确定的数.这样,当x变化时,
f ′(x)便是x的一个函数,我们称它为f (x)的导函数.即:f(x)在x=x0处的导数f (x)的导函数x=x0时的函数值1.能利用导数的定义推导函数y=c,y=x,y
=x2, y=x-1 , y= 的导数.
2.能根据基本初等函数的求导公式,求简单
函数的导数.(重点)探究点1 几种常见函数的导数根据导数的定义可以得出一些常见函数的导数公式.公式一:1.函数y=f(x)=c的导数.2.函数y=f(x)=x的导数3.函数y=f(x)=x2的导数探究点2 基本初等函数的导数公式
(1)若f(x)=c(c为常数),则 = ;
(2)若f(x)=xa (a∈Q*),则 = ;
(3)若f(x)=sin x,则 = ;
(4)若f(x)= cos x,则 = ;
(5)若f(x)=ax,则 = ;axln a cos x-sin x0(6)若f(x)=ex,则f′(x)=_____;
(7)若f(x)=logax,则f′(x)=_______;
(8)若f(x)=ln x,则f ′(x)=______.ex【变式练习】例2 求下列函数的导数
(1)y=a2(a为常数).
(2)y=x12.
(3)y=x-4.
(4)y=lg x.?【总结提升】(1)用导数的定义求导是求导数的基本方法,但运算较繁.利用常用函数的导数公式,可以简化求导过程,降低运算难度.
(2)利用导数公式求导,应根据所给问题的特征,恰当地选择求导公式,将题中函数的结构进行调整.如将根式、分式转化为指数式,利用幂函数的求导公式求导.??在确定与切线垂直的直线方程时,应注意考察函数在切点处的导数y′是否为零,当y′=0时,切线平行于x轴,过切点P垂直于切线的直线斜率不存在.【总结提升】1.选择题(1)下列各式正确的是( )C(2)下列各式正确的是( )D(1) f(x)=80,则f′(x)=______;2.填空0e+1(5)曲线y=xn在x=2处的导数为12,则n等于____.32.基本初等函数的导数公式
(1)若f (x)=c,则f′(x)=____;
(2)若f (x)=xa(a∈Q*),则f′(x)= ;
(3)若f (x)=sin x,则f′(x)=______;
(4)若f (x)= cos x,则f′(x)=_______;
(5)若f (x)=ax,则f′(x)=__________;axln acos x-sin x01.会求常用函数的导数.axa-1(6)若f (x)=e x,则f′(x)=____;
(7)若f (x)=logax,则f′(x)= ;
(8)若f (x)=ln x,则f′(x)=____.e x 业精于勤,荒于嬉;行成于思,毁于随.
——韩愈
与基本初等函数的导数公式 1.求函数在点x0处的导数的方法是:在不致发生混淆时,导函数也简称导数.2.导函数 当x=x0时, f ′(x0) 是一个确定的数.这样,当x变化时,
f ′(x)便是x的一个函数,我们称它为f (x)的导函数.即:f(x)在x=x0处的导数f (x)的导函数x=x0时的函数值1.能利用导数的定义推导函数y=c,y=x,y
=x2, y=x-1 , y= 的导数.
2.能根据基本初等函数的求导公式,求简单
函数的导数.(重点)探究点1 几种常见函数的导数根据导数的定义可以得出一些常见函数的导数公式.公式一:1.函数y=f(x)=c的导数.2.函数y=f(x)=x的导数3.函数y=f(x)=x2的导数探究点2 基本初等函数的导数公式
(1)若f(x)=c(c为常数),则 = ;
(2)若f(x)=xa (a∈Q*),则 = ;
(3)若f(x)=sin x,则 = ;
(4)若f(x)= cos x,则 = ;
(5)若f(x)=ax,则 = ;axln a cos x-sin x0(6)若f(x)=ex,则f′(x)=_____;
(7)若f(x)=logax,则f′(x)=_______;
(8)若f(x)=ln x,则f ′(x)=______.ex【变式练习】例2 求下列函数的导数
(1)y=a2(a为常数).
(2)y=x12.
(3)y=x-4.
(4)y=lg x.?【总结提升】(1)用导数的定义求导是求导数的基本方法,但运算较繁.利用常用函数的导数公式,可以简化求导过程,降低运算难度.
(2)利用导数公式求导,应根据所给问题的特征,恰当地选择求导公式,将题中函数的结构进行调整.如将根式、分式转化为指数式,利用幂函数的求导公式求导.??在确定与切线垂直的直线方程时,应注意考察函数在切点处的导数y′是否为零,当y′=0时,切线平行于x轴,过切点P垂直于切线的直线斜率不存在.【总结提升】1.选择题(1)下列各式正确的是( )C(2)下列各式正确的是( )D(1) f(x)=80,则f′(x)=______;2.填空0e+1(5)曲线y=xn在x=2处的导数为12,则n等于____.32.基本初等函数的导数公式
(1)若f (x)=c,则f′(x)=____;
(2)若f (x)=xa(a∈Q*),则f′(x)= ;
(3)若f (x)=sin x,则f′(x)=______;
(4)若f (x)= cos x,则f′(x)=_______;
(5)若f (x)=ax,则f′(x)=__________;axln acos x-sin x01.会求常用函数的导数.axa-1(6)若f (x)=e x,则f′(x)=____;
(7)若f (x)=logax,则f′(x)= ;
(8)若f (x)=ln x,则f′(x)=____.e x 业精于勤,荒于嬉;行成于思,毁于随.
——韩愈
