1.3.1 函数的单调性与导数 课件1
文档属性
| 名称 | 1.3.1 函数的单调性与导数 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 900.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 19:07:56 | ||
图片预览






文档简介
课件27张PPT。1.3 导数在研究函数中的应用
1.3.1 函数的单调性与导数 过山车是一项富有刺激性的娱乐工具.那种风驰电掣、有惊无险的快感令不少人着迷. 过山车在设计过程中用到了那些数学知识呢,本节课我们就研究一下导数在实际生活中的应用吧!1.正确理解利用导数判断函数的单调性的原理. (重点)
2.利用导数判断函数单调性.(难点)
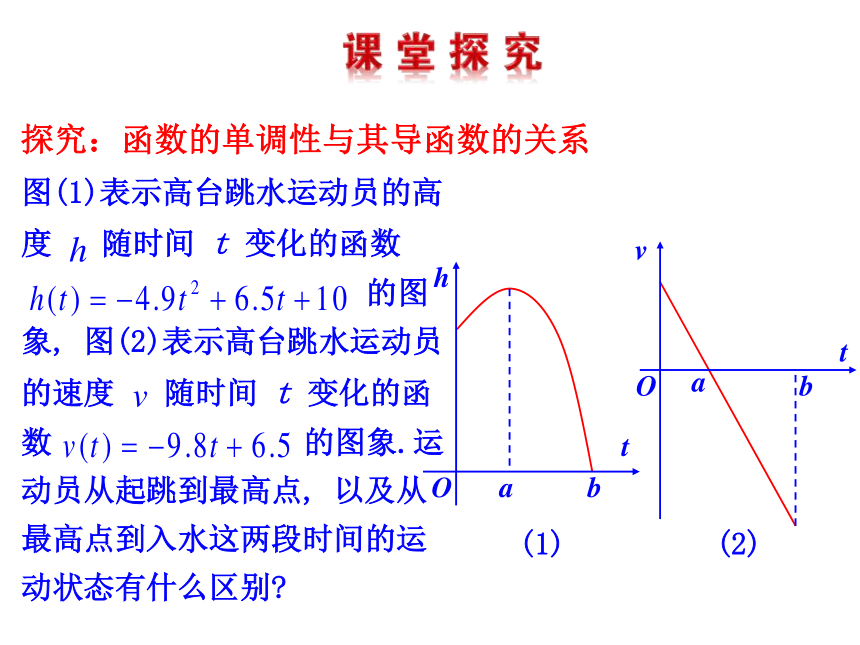
3.掌握利用导数判断函数单调性的方法.图(1)表示高台跳水运动员的高
度 随时间 t 变化的函数
的图
象, 图(2)表示高台跳水运动员
的速度 随时间 t 变化的函
数 的图象.运
动员从起跳到最高点, 以及从
最高点到入水这两段时间的运
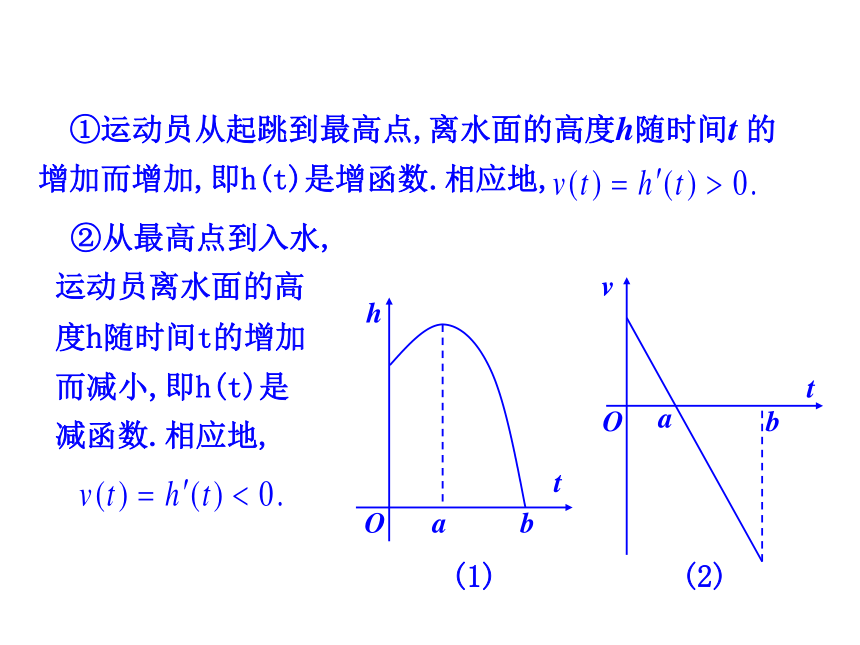
动状态有什么区别?aabbttvhOO(1)(2)探究:函数的单调性与其导函数的关系aabbttvhOO ①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地, ②从最高点到入水,
运动员离水面的高
度h随时间t的增加
而减小,即h(t)是
减函数.相应地,(1)(2)OOOO例1 已知导函数 的下列信息:当1 < x < 4 时,当 x > 4 , 或 x < 1时,当 x = 4 , 或 x = 1时,试画出函数f(x)图象的大致形状. 当 x > 4 , 或 x < 1时, 可知 在这两个区间内单调递减; 当 x = 4 , 或 x = 1时, 综上, 函数 图象的大致形状如图所示.y= 例2 判断下列函数的单调性, 并求出单调区间:因此, 函数 在
上单调递增.如图(1)所示单调递减单调递增单调递减根据导数确定函数的单调性步骤:1.确定函数f(x)的定义域.2.求出函数的导数.3.解不等式f′(x)>0,得函数单调增区间;
解不等式f′(x)<0,得函数单调减区间.总结提升例4 已知函数f(x)=ax3+3x2-x+1在(-∞,+∞)上是减函数,求实数a的取值范围.【解析】f′(x)=3ax2+6x-1,
由题意得3ax2+6x-1≤0在(-∞,+∞)上恒成立.
当a=0时,6x-1≤0,x≤ 不满足题意,∴a≠0.
当a≠0时,由题意得,
解得a≤-3.
综上可知,实数a的取值范围是a≤-3.1.函数y=3x-x3的单调增区间是( )
A.(0,+∞) B.(-∞,-1)
C.(-1,1) D.(1,+∞)C2.(2014·新课标全国2)若函数
在区间 单调递增,则k的取值范围是( )
A. B.
C. D.D3.函数y=xlnx在区间(0,1)上是( )
A.单调增函数
B.单调减函数
C.在(0, )上是减函数,在( , 1)上是增函数
D.在( , 1)上是减函数,在(0, )上是增函数C4.函数y=x2(x+3)的单调递减区间是 ,
单调递增区间是 .(-2,0) (-∞,-2),(0,+∞) 5.函数f(x)=cos2x的单调递减区间是
.(kπ, kπ+ ), k∈Z 1.求可导函数f(x)单调区间的步骤:
(1)求
(2)解不等式 >0(或 <0)
(3)确认并指出递增区间(或递减区间)2.证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求
(2)确认 在(a,b)内的符号
(3)作出结论 古之成大事者,不惟有超世之才,亦必有坚忍不拔之志也.
1.3.1 函数的单调性与导数 过山车是一项富有刺激性的娱乐工具.那种风驰电掣、有惊无险的快感令不少人着迷. 过山车在设计过程中用到了那些数学知识呢,本节课我们就研究一下导数在实际生活中的应用吧!1.正确理解利用导数判断函数的单调性的原理. (重点)
2.利用导数判断函数单调性.(难点)
3.掌握利用导数判断函数单调性的方法.图(1)表示高台跳水运动员的高
度 随时间 t 变化的函数
的图
象, 图(2)表示高台跳水运动员
的速度 随时间 t 变化的函
数 的图象.运
动员从起跳到最高点, 以及从
最高点到入水这两段时间的运
动状态有什么区别?aabbttvhOO(1)(2)探究:函数的单调性与其导函数的关系aabbttvhOO ①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地, ②从最高点到入水,
运动员离水面的高
度h随时间t的增加
而减小,即h(t)是
减函数.相应地,(1)(2)OOOO例1 已知导函数 的下列信息:当1 < x < 4 时,当 x > 4 , 或 x < 1时,当 x = 4 , 或 x = 1时,试画出函数f(x)图象的大致形状. 当 x > 4 , 或 x < 1时, 可知 在这两个区间内单调递减; 当 x = 4 , 或 x = 1时, 综上, 函数 图象的大致形状如图所示.y= 例2 判断下列函数的单调性, 并求出单调区间:因此, 函数 在
上单调递增.如图(1)所示单调递减单调递增单调递减根据导数确定函数的单调性步骤:1.确定函数f(x)的定义域.2.求出函数的导数.3.解不等式f′(x)>0,得函数单调增区间;
解不等式f′(x)<0,得函数单调减区间.总结提升例4 已知函数f(x)=ax3+3x2-x+1在(-∞,+∞)上是减函数,求实数a的取值范围.【解析】f′(x)=3ax2+6x-1,
由题意得3ax2+6x-1≤0在(-∞,+∞)上恒成立.
当a=0时,6x-1≤0,x≤ 不满足题意,∴a≠0.
当a≠0时,由题意得,
解得a≤-3.
综上可知,实数a的取值范围是a≤-3.1.函数y=3x-x3的单调增区间是( )
A.(0,+∞) B.(-∞,-1)
C.(-1,1) D.(1,+∞)C2.(2014·新课标全国2)若函数
在区间 单调递增,则k的取值范围是( )
A. B.
C. D.D3.函数y=xlnx在区间(0,1)上是( )
A.单调增函数
B.单调减函数
C.在(0, )上是减函数,在( , 1)上是增函数
D.在( , 1)上是减函数,在(0, )上是增函数C4.函数y=x2(x+3)的单调递减区间是 ,
单调递增区间是 .(-2,0) (-∞,-2),(0,+∞) 5.函数f(x)=cos2x的单调递减区间是
.(kπ, kπ+ ), k∈Z 1.求可导函数f(x)单调区间的步骤:
(1)求
(2)解不等式 >0(或 <0)
(3)确认并指出递增区间(或递减区间)2.证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求
(2)确认 在(a,b)内的符号
(3)作出结论 古之成大事者,不惟有超世之才,亦必有坚忍不拔之志也.
