1.3.2 函数的极值与导数 课件1
文档属性
| 名称 | 1.3.2 函数的极值与导数 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 19:14:56 | ||
图片预览








文档简介
课件49张PPT。1.3.2 函数的极值与导数 自主学习 新知突破1.了解函数极值的概念,会从几何的角度直观理解函数的极值与导数的关系,并会灵活应用.
2.掌握函数极值的判定及求法.
3.掌握函数在某一点取得极值的条件.
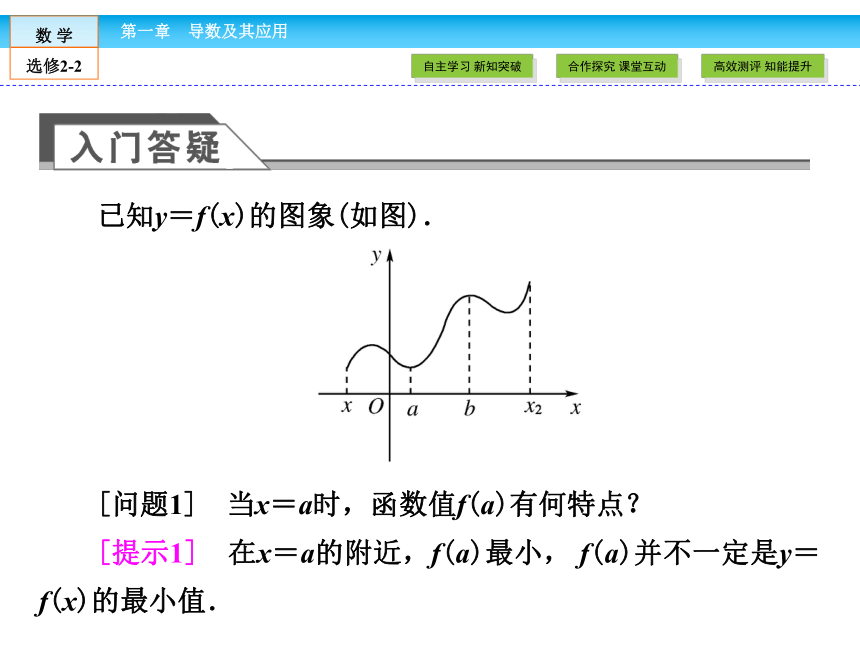
4.增强数形结合的思维意识,提高运用导数的基本思想去分析和解决实际问题的能力.已知y=f(x)的图象(如图).
[问题1] 当x=a时,函数值f(a)有何特点?
[提示1] 在x=a的附近,f(a)最小, f(a)并不一定是y=f(x)的最小值.
[问题2] 试分析在x=a的附近导数的符号.
[提示2] 在x=a附近的左侧,曲线的切线斜率小于零,即f′(x)<0,而在x=a附近的右侧,曲线的切线斜率大于零,即f′(x)>0.
[问题3] f′(a)值是什么?
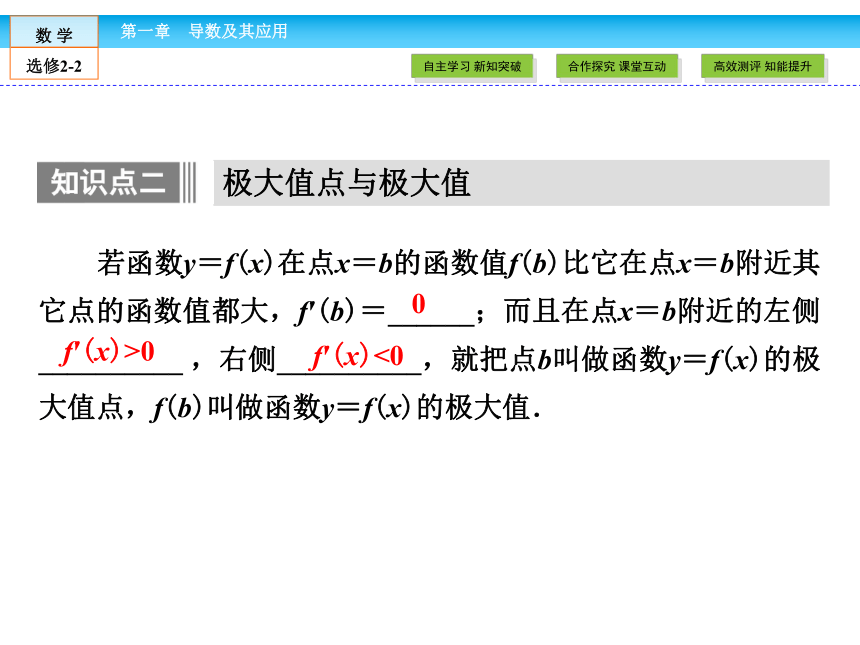
[提示3] f′(a)=0.若函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其它点的函数值都小,f′(a)=_______;而且在点x=a附近的左侧__________,右侧__________,就把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.极小值点与极小值 0f′(x)<0f′(x)>0若函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其它点的函数值都大,f′(b)=______;而且在点x=b附近的左侧__________ ,右侧__________,就把点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.极大值点与极大值 0f′(x)>0f′(x)<01.对函数极值概念的理解
(1)函数的极值是函数的局部性质,它反映了函数在某一点附近的大小情况.
(2)由函数极值的定义知道,函数在一个区间的端点处一定不可能取得极值,即端点一定不是函数的极值点.
(3)在一个给定的区间上,函数可能有若干个极值点,也可能不存在极值点;函数可能只有极大值,没有极小值,或者只有极小值,没有极大值,也可能既有极大值,又有极小值.极大值不一定比极小值大,极小值也不一定比极大值小.求函数y=f(x)的极值的方法是:
解方程f′(x)=0,当f′(x0)=0时
(1)如果在x0附近的左侧__________,右侧__________,那么,f(x0)是极大值.
(2)如果在x0附近的左侧__________,右侧__________,那么,f(x0)是极小值.函数极值的求法 f′(x)>0f′(x)<0f′(x)<0f′(x)>02.极值点与导数的关系
(1)可导函数的极值点必须是导数为0的点,但导数为0的点不一定是极值点.
(2)不可导点可能是极值点,也可能不是极值点.
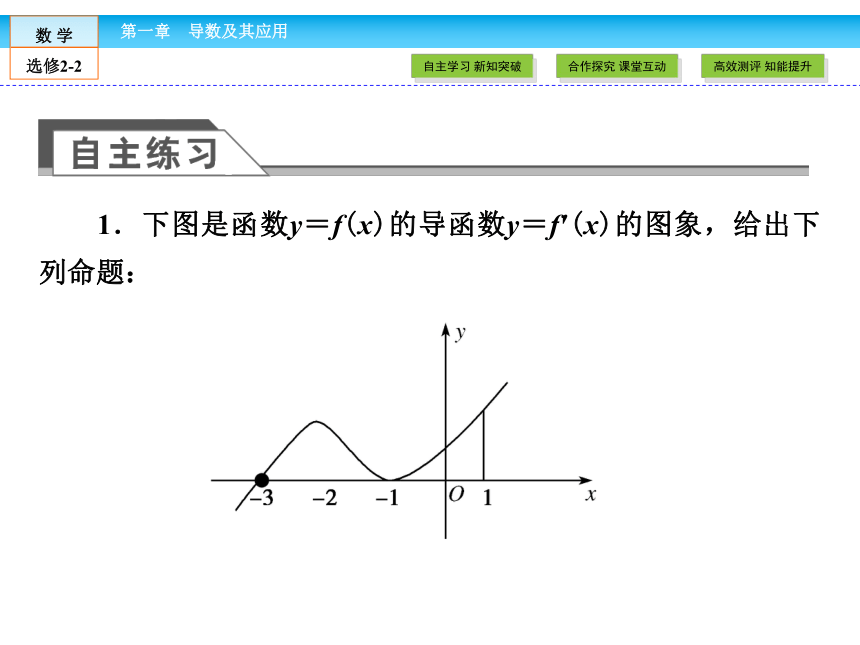
(3)导数为0是极值点:y=x2,y′(0)=0,x=0是极小值点.1.下图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
①-3是函数y=f(x)的极值点;
②-1是函数y=f(x)的最小值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(-3,1)上单调递增.
则正确命题的序号是( )
A.①② B.①④
C.②③ D.③④
解析: 由导函数图象知函数f(x)在(-∞,-3)上单调递减,(-3,+∞)上单调递增,f′(-3)=0,f′(0)>0,x=-3是函数f(x)的极值点,①④正确.
答案: B
2.函数y=(x2-1)3+1的极值点是( )
A.极大值点x=-1 B.极大值点x=0
C.极小值点x=0 D.极小值点x=1
解析: y′=6x(x2-1)2=0有三个根,x1=-1,x2=0,x3=1,由解y′>0得x>0;由解y′<0得x<0,只有x=0是极小值点,故选C.
答案: C3.函数f(x)=x3-3x2+1的极小值点为________.
解析: 由f′(x)=3x2-6x=0,
解得x=0或x=2.
列表如下:
∴当x=2时,f(x)取得极小值.
答案: x=2合作探究 课堂互动 求函数的极值 求下列函数的极值:
[思路点拨] 先确定函数定义域,然后正确求导,再解方程f′(x)=0,列表分析,求出函数的极值. (1)函数的定义域为R.
f′(x)=x2-2x-3=(x+1)(x-3).
令f′(x)=0,得x1=-1,x2=3.
由此可知当x变化时,f′(x),f(x)的变化情况如下表所示:
当x变化时,f′(x)与f(x)的变化情况如下表:
故当x=3时函数取得极小值,且f(3)=-22. 1.求可导函数f(x)极值的步骤:
(1)求函数的导数f′(x);
(2)令f′(x)=0,求出全部的根x0;
(3)列表,方程的根x0将整个定义域分成若干个区间,把x,f′(x),f(x)在每个区间内的变化情况列在这个表格内;
(4)判断得结论,若导数在x0附近左正右负,则在x0处取得极大值;若左负右正,则取得极小值.
2.注意事项:
(1)不要忽略函数的定义域;
(2)要正确地列出表格,不要遗漏区间和分界点.1.求下列函数的极值:
(1)f(x)=x3-12x;
(2)f(x)=x2e-x.
解析: (1)函数f(x)的定义域为R.
f′(x)=3x2-12=3(x+2)(x-2).
令f′(x)=0,得x=-2或x=2.当x变化时,f′(x),f(x)的变化情况如下表:
从表中可以看出,当x=-2时,函数f(x)有极大值,
且f(-2)=(-2)3-12×(-2)=16;
当x=2时,函数f(x)有极小值,
且f(2)=23-12×2=-16.
(2)函数f(x)的定义域为R.
f′(x)=2xe-x+x2e-x(-x)′=2xe-x-x2e-x
=x(2-x)e-x.
令f′(x)=0,得x=0或x=2.已知函数极值求参数 设函数f(x)=ax3+bx2+cx,在x=1和x=-1处有极值,且f(1)=-1,求a,b,c的值,并求出相应的极值.
根据x=±1列表分析f′(x)的符号,f(x)的单调性和极值点.
由上表可以看出,
当x=-1时,函数有极大值,且f(-1)=1;
当x=1时,函数有极小值,且f(1)=-1. 已知函数极值情况,逆向应用确定函数的解析式,进而研究函数性质时,注意两点:
(1)常根据极值点处导数为0和极值两个条件列方程组,利用待定系数法求解;
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.
2.已知函数f(x)=x3+ax2+bx+c,当x=-1时,取得极大值7;当x=3时,取得极小值.求这个极小值及a,b,c的值.
解析: f′(x)=3x2+2ax+b.
据题意,-1,3是方程3x2+2ax+b=0的两个根,
由根与系数的关系得极值的综合应用 已知a为实数,函数f(x)=-x3+3x+a.
(1)求函数f(x)的极值,并画出其图象(草图);
(2)当a为何值时,方程f(x)=0恰好有两个实数根?[思路点拨]
(2)结合图象,当极大值a+2=0时,有极小值小于0,此时曲线f(x)与x轴恰有两个交点,即方程f(x)=0恰有两个实数根,所以a=-2满足条件;当极小值a-2=0时,有极大值大于0,此时曲线f(x)与x轴恰有两个交点,即方程f(x)=0恰好有两个实数根,所以a=2满足条件.
综上,当a=±2时,方程恰有两个实数根. 12分 1.如何利用导数画函数的大致图象?
求出函数的极值点和极值,结合函数的单调性及x→∞时,f(x)值的变化趋势,可画出函数的大致图象.
2.如何利用导数判断方程根的个数?
用求导的方法确定方程根的个数,是一种很有效的方法.它通过函数的变化情况,运用数形结合思想来确定函数图象与x轴的交点个数,从而判断方程根的个数. 3.将本例中(2)改为:
①f(x)=0恰有三个实数根;②若只有一个实数根.
求实数a的取值范围.
②若f(x)=0恰有一个实数根,如图(2)则有:
a-2>0,解得a>2,或a+2<0,解得a<-2.
故①-2②a>2,或a<-2时,f(x)=0只有一个实数根.◎已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a,b的值.【错因】 根据极值的定义,函数先减后增为极小值,函数先增后减为极大值,此题未验证x=-1两侧函数的单调性,故求错.
当a=1,b=3时,f′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去.
当a=2,b=9时,f′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈(-∞,-3)时,f(x)为增函数;
当x∈(-3,-1)时,f(x)为减函数;
当x∈(-1,+∞)时,f(x)为增函数.
所以f(x)在x=-1时取得极小值,
因此a=2,b=9.高效测评 知能提升 完成练习册作业谢谢观看!
2.掌握函数极值的判定及求法.
3.掌握函数在某一点取得极值的条件.
4.增强数形结合的思维意识,提高运用导数的基本思想去分析和解决实际问题的能力.已知y=f(x)的图象(如图).
[问题1] 当x=a时,函数值f(a)有何特点?
[提示1] 在x=a的附近,f(a)最小, f(a)并不一定是y=f(x)的最小值.
[问题2] 试分析在x=a的附近导数的符号.
[提示2] 在x=a附近的左侧,曲线的切线斜率小于零,即f′(x)<0,而在x=a附近的右侧,曲线的切线斜率大于零,即f′(x)>0.
[问题3] f′(a)值是什么?
[提示3] f′(a)=0.若函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其它点的函数值都小,f′(a)=_______;而且在点x=a附近的左侧__________,右侧__________,就把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.极小值点与极小值 0f′(x)<0f′(x)>0若函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其它点的函数值都大,f′(b)=______;而且在点x=b附近的左侧__________ ,右侧__________,就把点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.极大值点与极大值 0f′(x)>0f′(x)<01.对函数极值概念的理解
(1)函数的极值是函数的局部性质,它反映了函数在某一点附近的大小情况.
(2)由函数极值的定义知道,函数在一个区间的端点处一定不可能取得极值,即端点一定不是函数的极值点.
(3)在一个给定的区间上,函数可能有若干个极值点,也可能不存在极值点;函数可能只有极大值,没有极小值,或者只有极小值,没有极大值,也可能既有极大值,又有极小值.极大值不一定比极小值大,极小值也不一定比极大值小.求函数y=f(x)的极值的方法是:
解方程f′(x)=0,当f′(x0)=0时
(1)如果在x0附近的左侧__________,右侧__________,那么,f(x0)是极大值.
(2)如果在x0附近的左侧__________,右侧__________,那么,f(x0)是极小值.函数极值的求法 f′(x)>0f′(x)<0f′(x)<0f′(x)>02.极值点与导数的关系
(1)可导函数的极值点必须是导数为0的点,但导数为0的点不一定是极值点.
(2)不可导点可能是极值点,也可能不是极值点.
(3)导数为0是极值点:y=x2,y′(0)=0,x=0是极小值点.1.下图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
①-3是函数y=f(x)的极值点;
②-1是函数y=f(x)的最小值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(-3,1)上单调递增.
则正确命题的序号是( )
A.①② B.①④
C.②③ D.③④
解析: 由导函数图象知函数f(x)在(-∞,-3)上单调递减,(-3,+∞)上单调递增,f′(-3)=0,f′(0)>0,x=-3是函数f(x)的极值点,①④正确.
答案: B
2.函数y=(x2-1)3+1的极值点是( )
A.极大值点x=-1 B.极大值点x=0
C.极小值点x=0 D.极小值点x=1
解析: y′=6x(x2-1)2=0有三个根,x1=-1,x2=0,x3=1,由解y′>0得x>0;由解y′<0得x<0,只有x=0是极小值点,故选C.
答案: C3.函数f(x)=x3-3x2+1的极小值点为________.
解析: 由f′(x)=3x2-6x=0,
解得x=0或x=2.
列表如下:
∴当x=2时,f(x)取得极小值.
答案: x=2合作探究 课堂互动 求函数的极值 求下列函数的极值:
[思路点拨] 先确定函数定义域,然后正确求导,再解方程f′(x)=0,列表分析,求出函数的极值. (1)函数的定义域为R.
f′(x)=x2-2x-3=(x+1)(x-3).
令f′(x)=0,得x1=-1,x2=3.
由此可知当x变化时,f′(x),f(x)的变化情况如下表所示:
当x变化时,f′(x)与f(x)的变化情况如下表:
故当x=3时函数取得极小值,且f(3)=-22. 1.求可导函数f(x)极值的步骤:
(1)求函数的导数f′(x);
(2)令f′(x)=0,求出全部的根x0;
(3)列表,方程的根x0将整个定义域分成若干个区间,把x,f′(x),f(x)在每个区间内的变化情况列在这个表格内;
(4)判断得结论,若导数在x0附近左正右负,则在x0处取得极大值;若左负右正,则取得极小值.
2.注意事项:
(1)不要忽略函数的定义域;
(2)要正确地列出表格,不要遗漏区间和分界点.1.求下列函数的极值:
(1)f(x)=x3-12x;
(2)f(x)=x2e-x.
解析: (1)函数f(x)的定义域为R.
f′(x)=3x2-12=3(x+2)(x-2).
令f′(x)=0,得x=-2或x=2.当x变化时,f′(x),f(x)的变化情况如下表:
从表中可以看出,当x=-2时,函数f(x)有极大值,
且f(-2)=(-2)3-12×(-2)=16;
当x=2时,函数f(x)有极小值,
且f(2)=23-12×2=-16.
(2)函数f(x)的定义域为R.
f′(x)=2xe-x+x2e-x(-x)′=2xe-x-x2e-x
=x(2-x)e-x.
令f′(x)=0,得x=0或x=2.已知函数极值求参数 设函数f(x)=ax3+bx2+cx,在x=1和x=-1处有极值,且f(1)=-1,求a,b,c的值,并求出相应的极值.
根据x=±1列表分析f′(x)的符号,f(x)的单调性和极值点.
由上表可以看出,
当x=-1时,函数有极大值,且f(-1)=1;
当x=1时,函数有极小值,且f(1)=-1. 已知函数极值情况,逆向应用确定函数的解析式,进而研究函数性质时,注意两点:
(1)常根据极值点处导数为0和极值两个条件列方程组,利用待定系数法求解;
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.
2.已知函数f(x)=x3+ax2+bx+c,当x=-1时,取得极大值7;当x=3时,取得极小值.求这个极小值及a,b,c的值.
解析: f′(x)=3x2+2ax+b.
据题意,-1,3是方程3x2+2ax+b=0的两个根,
由根与系数的关系得极值的综合应用 已知a为实数,函数f(x)=-x3+3x+a.
(1)求函数f(x)的极值,并画出其图象(草图);
(2)当a为何值时,方程f(x)=0恰好有两个实数根?[思路点拨]
(2)结合图象,当极大值a+2=0时,有极小值小于0,此时曲线f(x)与x轴恰有两个交点,即方程f(x)=0恰有两个实数根,所以a=-2满足条件;当极小值a-2=0时,有极大值大于0,此时曲线f(x)与x轴恰有两个交点,即方程f(x)=0恰好有两个实数根,所以a=2满足条件.
综上,当a=±2时,方程恰有两个实数根. 12分 1.如何利用导数画函数的大致图象?
求出函数的极值点和极值,结合函数的单调性及x→∞时,f(x)值的变化趋势,可画出函数的大致图象.
2.如何利用导数判断方程根的个数?
用求导的方法确定方程根的个数,是一种很有效的方法.它通过函数的变化情况,运用数形结合思想来确定函数图象与x轴的交点个数,从而判断方程根的个数. 3.将本例中(2)改为:
①f(x)=0恰有三个实数根;②若只有一个实数根.
求实数a的取值范围.
②若f(x)=0恰有一个实数根,如图(2)则有:
a-2>0,解得a>2,或a+2<0,解得a<-2.
故①-2
当a=1,b=3时,f′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去.
当a=2,b=9时,f′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈(-∞,-3)时,f(x)为增函数;
当x∈(-3,-1)时,f(x)为减函数;
当x∈(-1,+∞)时,f(x)为增函数.
所以f(x)在x=-1时取得极小值,
因此a=2,b=9.高效测评 知能提升 完成练习册作业谢谢观看!
