1.3.3 函数的最大(小)值与导数 课件1
文档属性
| 名称 | 1.3.3 函数的最大(小)值与导数 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 536.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 19:19:12 | ||
图片预览







文档简介
课件22张PPT。1.3.3 函数的最大(小)值与导数 汽油的消耗量(单位:L)与
汽车的速度(单位:km/h)
之间有一定的关系,汽油的
消耗量是汽车速度的函数.
根据你的生活经验,思考
下面两个问题:
(1)是不是汽车的速度越快,汽油的消耗量越大 ; (2)“汽油的使用率最高”的含义是什么?
解析:(1)显然不是;
(2)行驶里程一定,汽油消耗量最小.
今天我们来学习有关最大值与最小值的问题! 飞驰的汽车1.借助函数图象,直观地理解函数的最大值和
最小值概念.
2.弄清函数最大值、最小值与极大值、极小值
的区别与联系,理解和熟悉函数必有最大值
和最小值的充分条件.(重点)
3.掌握求在闭区间上连续的函数的最大值和
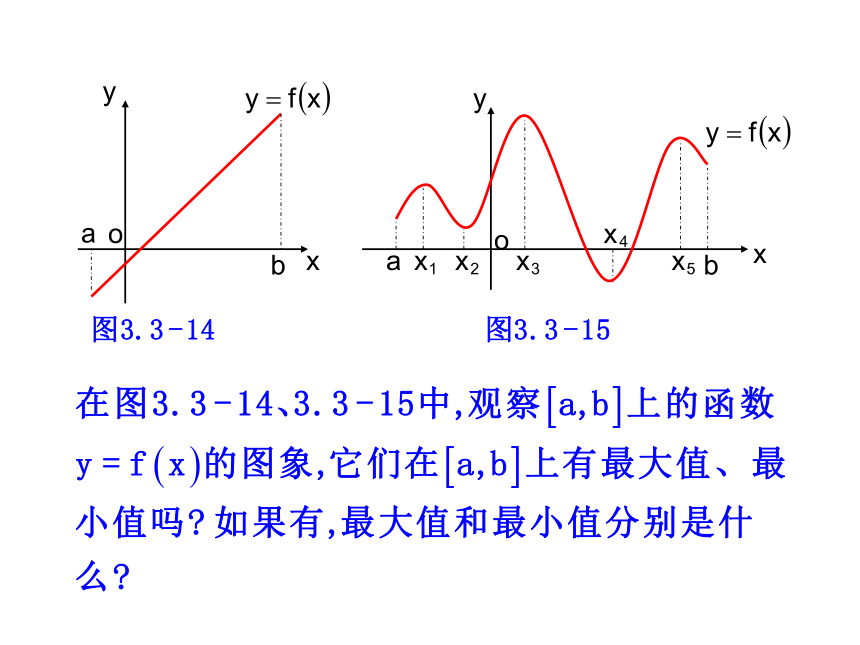
最小值的思想方法和步骤.(难点) 在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高、效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题. 函数在什么条件下一定有最大、最小值?它们与函数极值关系如何? 极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小.探究点 函数的最大(小)值与导数
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: 最大值与最小值的概念 (1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最大值. 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≥M;
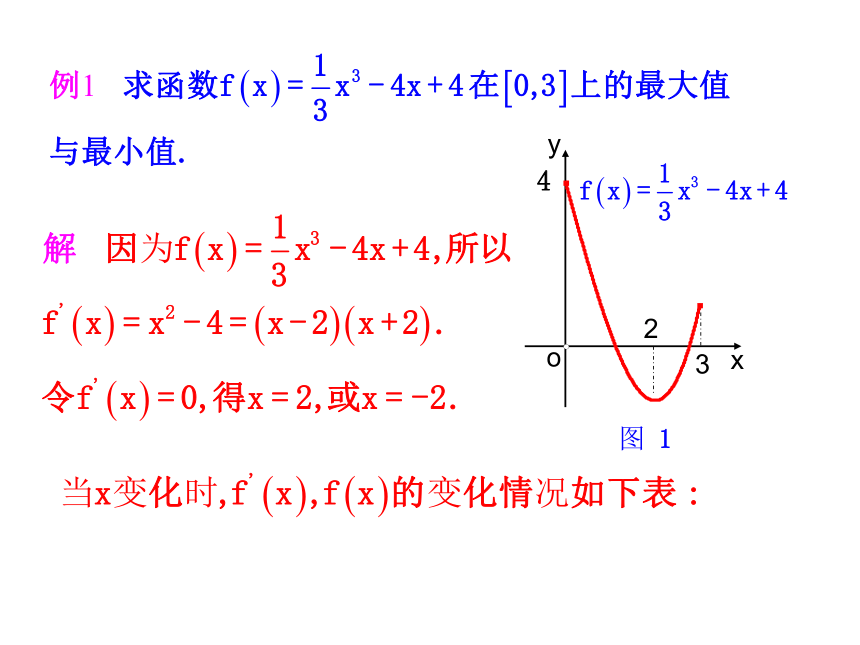
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最小值. 4例2 求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.解:令 ,解得x=-1,0,1.当x变化时, 的变化情况如下表:从上表可知,最大值是13,最小值是4.1345↗4↘130-0+0-2(1,2)1(0,1)0(-1,0)-1(-2,-1)-2+↘↗1.函数的最值概念是全局性的2.函数的最大值(最小值)唯一3.函数的最值可在端点处取得总结提升函数f(x)=x3-3x+1在闭区间[-3,0]上的最大值、
最小值分别是( )
1,-1 B. 1,-17
C. 3,-17 D. 9,-19C2.函数f(x)的定义域为R,导函数f′(x)的图象
如图,则函数f(x)( )
无极大值点,有两个极小值点
有三个极大值点,两个极小值点
有两个极大值点,两个极小值点
有四个极大值点,
无极小值点C 3.设函数 则 ( )
A.有最大值 B.有最小值
C.是增函数 D.是减函数AA5.已知f(x)=2x3-6x2+m(m为常数),在[-2 , 2]上
有最大值3,函数在[-2 , 2]上的最小值为____.-376.函数f(x)=x3+ax+b,满足f(0)=0,且在x=1时取
得极小值,则实数a的值为_____.-37.若函数 的最大值为3,最小值为-29,求a,b的值. 解:令 得x=0, x=4(舍去).当x变化时, ,f(x)的变化情况如下表:由表知,当x=0时,f(x)取得最大值b,故b=3.又f(-1)-f(2)=9a>0,
所以f(x)的最小值为f(2)=-16a+3=-29,故a=2.1.求在[a,b]上连续,(a,b)上可导的函数f(x)在[a,b]上的最值的步骤:
(1)求f(x)在(a,b)内的极值;
(2)将f(x)的各极值与f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.一是利用函数性质
二是利用不等式
三是利用导数 2.求函数最值的一般方法:3.求函数的最值时,应注意以下几点:(1)要正确区分极值与最值这两个概念.(2)在[a,b]上连续,(a,b)上可导的函数f(x)在(a,b)内未必有最大值与最小值.(3)一旦给出的函数在(a,b)上有个别不可导点的话,不要忘记在步骤(2)中,要把这些点的函数值与各极值和f(a),f(b)放在一起比较.苦心人,天不负,卧薪尝胆,三千越甲可吞吴.
汽车的速度(单位:km/h)
之间有一定的关系,汽油的
消耗量是汽车速度的函数.
根据你的生活经验,思考
下面两个问题:
(1)是不是汽车的速度越快,汽油的消耗量越大 ; (2)“汽油的使用率最高”的含义是什么?
解析:(1)显然不是;
(2)行驶里程一定,汽油消耗量最小.
今天我们来学习有关最大值与最小值的问题! 飞驰的汽车1.借助函数图象,直观地理解函数的最大值和
最小值概念.
2.弄清函数最大值、最小值与极大值、极小值
的区别与联系,理解和熟悉函数必有最大值
和最小值的充分条件.(重点)
3.掌握求在闭区间上连续的函数的最大值和
最小值的思想方法和步骤.(难点) 在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高、效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题. 函数在什么条件下一定有最大、最小值?它们与函数极值关系如何? 极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小.探究点 函数的最大(小)值与导数
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: 最大值与最小值的概念 (1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最大值. 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)对于任意的x∈I,都有f(x)≥M;
(2)存在x0∈I,使得f(x0) = M那么,称M是函数y=f(x)的最小值. 4例2 求函数y=x4-2x2+5在区间[-2,2]上的最大值与最小值.解:令 ,解得x=-1,0,1.当x变化时, 的变化情况如下表:从上表可知,最大值是13,最小值是4.1345↗4↘130-0+0-2(1,2)1(0,1)0(-1,0)-1(-2,-1)-2+↘↗1.函数的最值概念是全局性的2.函数的最大值(最小值)唯一3.函数的最值可在端点处取得总结提升函数f(x)=x3-3x+1在闭区间[-3,0]上的最大值、
最小值分别是( )
1,-1 B. 1,-17
C. 3,-17 D. 9,-19C2.函数f(x)的定义域为R,导函数f′(x)的图象
如图,则函数f(x)( )
无极大值点,有两个极小值点
有三个极大值点,两个极小值点
有两个极大值点,两个极小值点
有四个极大值点,
无极小值点C 3.设函数 则 ( )
A.有最大值 B.有最小值
C.是增函数 D.是减函数AA5.已知f(x)=2x3-6x2+m(m为常数),在[-2 , 2]上
有最大值3,函数在[-2 , 2]上的最小值为____.-376.函数f(x)=x3+ax+b,满足f(0)=0,且在x=1时取
得极小值,则实数a的值为_____.-37.若函数 的最大值为3,最小值为-29,求a,b的值. 解:令 得x=0, x=4(舍去).当x变化时, ,f(x)的变化情况如下表:由表知,当x=0时,f(x)取得最大值b,故b=3.又f(-1)-f(2)=9a>0,
所以f(x)的最小值为f(2)=-16a+3=-29,故a=2.1.求在[a,b]上连续,(a,b)上可导的函数f(x)在[a,b]上的最值的步骤:
(1)求f(x)在(a,b)内的极值;
(2)将f(x)的各极值与f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.一是利用函数性质
二是利用不等式
三是利用导数 2.求函数最值的一般方法:3.求函数的最值时,应注意以下几点:(1)要正确区分极值与最值这两个概念.(2)在[a,b]上连续,(a,b)上可导的函数f(x)在(a,b)内未必有最大值与最小值.(3)一旦给出的函数在(a,b)上有个别不可导点的话,不要忘记在步骤(2)中,要把这些点的函数值与各极值和f(a),f(b)放在一起比较.苦心人,天不负,卧薪尝胆,三千越甲可吞吴.
