1.3.3 函数的最大(小)值与导数 课件2
文档属性
| 名称 | 1.3.3 函数的最大(小)值与导数 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 00:00:00 | ||
图片预览











文档简介
课件61张PPT。1.3.3
函数的最大(小)值与导数1.函数y=f(x)在闭区间[a,b]上取得最值的条件
如果在区间[a,b]上函数y=f(x)的图象是_____________的曲
线,那么它必有最大值和最小值.
2.求函数y=f(x)在[a,b]上的最大值与最小值的步骤
(1)求函数y=f(x)在_______内的极值.
(2)将函数y=f(x)的_______与端点处的_________________比
较,其中_____的一个是最大值,_____的一个是最小值.一条连续不断(a,b)各极值函数值f(a),f(b)最大最小1.判一判(正确的打“√”,错误的打“×”)
(1)函数的最大值一定是函数的极大值.( )
(2)开区间上的单调连续函数无最值.( )
(3)函数f(x)在区间[a,b]上的最大值和最小值一定在两个端点处取得.( )【解析】(1)错误.最大值也可能是端点的值.
(2)正确.在开区间上的单调函数无极值且端点处函数值取不到,故无最值.
(3)错误.函数f(x)在[a,b]上的最大值和最小值也有可能在区间内部某个极值点处取得.
答案:(1)× (2)√ (3)×2.做一做(请把正确的答案写在横线上)
(1)设函数f(x)=e2x+3x(x∈R),则f(x)__________(填“有”或“无”)最值.
(2)已知函数y=x3-x2-x,该函数在区间[0,3]上的最大值是__________.
(3)已知函数f(x)=-x3+3x2+m(x∈[-2,2]),f(x)的最小值为1,则m=__________.【解析】(1)因为函数f(x)=e2x+3x(x∈R),所以f′(x)=2e2x+3>0,所以函数f(x)在R上单调递增,没有最值.
答案:无
(2)y′=3x2-2x-1=(3x+1)(x-1),
当0≤x<1时,y′<0,当10,
所以当x=1时,y取得极小值,即最小值,为-1,
又当x=0时,y=0,当x=3时,y=15,
所以该函数在区间[0,3]上的最大值是15.
答案:15(3)f′(x)=-3x2+6x=-3x(x-2),令f′(x)=0,解得x=0或x=2.当x∈[-2,2]时,解f′(x)<0,得-2≤x<0;解f′(x)>0,得0答案:1【要点探究】
知识点 函数的最大(小)值与导数
1.对函数最值的三点说明
(1)闭区间上的连续函数一定有最值,开区间内的连续函数不一定有最值.若有惟一的极值,则此极值必是函数的最值.
(2)函数的最大值和最小值是一个整体性概念.
(3)函数y=f(x)在[a,b]上连续,是函数y=f(x)在[a,b]上有最大值或最小值的充分而非必要条件.2.函数极值与最值的关系
(1)函数的极值是函数在某一点附近的局部概念,函数的最大值和最小值是一个整体性概念.
(2)函数的最大值、最小值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,函数的极值可以有多个,但最值只能有一个.
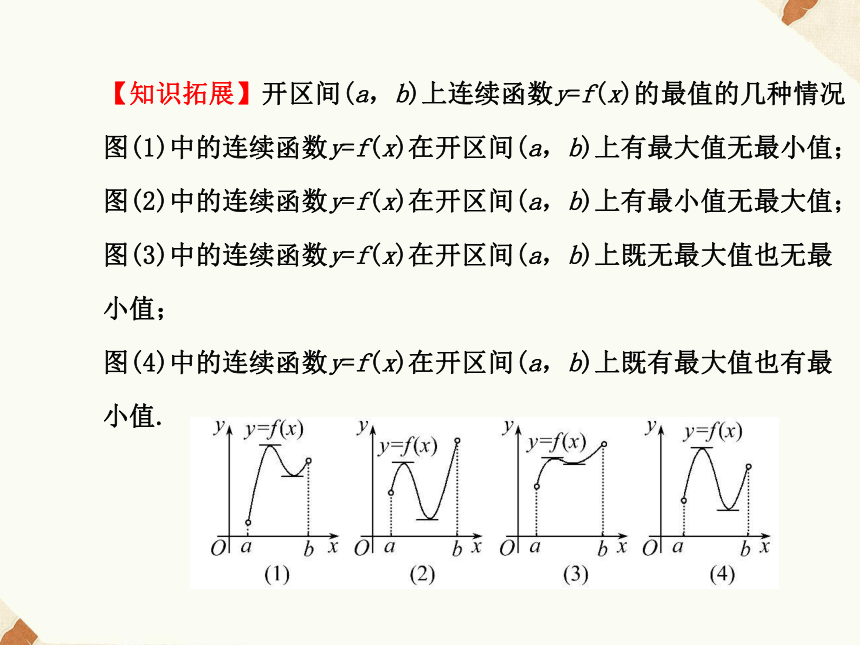
(3)极值只能在区间内取得,最值则可以在端点处取得.有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值不在端点处取得时必定是极值.【知识拓展】开区间(a,b)上连续函数y=f(x)的最值的几种情况
图(1)中的连续函数y=f(x)在开区间(a,b)上有最大值无最小值;
图(2)中的连续函数y=f(x)在开区间(a,b)上有最小值无最大值;
图(3)中的连续函数y=f(x)在开区间(a,b)上既无最大值也无最
小值;
图(4)中的连续函数y=f(x)在开区间(a,b)上既有最大值也有最
小值.【微思考】
(1)函数的极值是否一定是函数的最值?
提示:不一定.端点值也可能是函数的最值.
(2)如果在开区间(a,b)上的连续函数y=f(x)只有一个极值且为极小值,那么函数在开区间(a,b)上有最值吗?
提示:有最小值,无最大值.若x0是函数的极值点,则函数在(a,x0)是减函数,在(x0,b)是增函数,故f(x)在x=x0处取得最小值.【即时练】
关于函数f(x)=(2x-x2)ex,则下列四个结论:
①f(x)>0的解集为{x|0②f(x)的极小值为f(- ),极大值为f( );
③f(x)没有最小值,也没有最大值;
④f(x)没有最小值,有最大值.
其中正确结论为( )
A.①②④ B.①②③ C.①③ D.②④【解析】选A.由f(x)>0可得(2x-x2)ex>0,
因为ex>0,所以2x-x2>0,所以0f′(x)=ex(2-x2),由f′(x)=0得x=± ,
由f′(x)<0得,x> 或x<- ,
由f′(x)>0得,-所以f(x)的单调减区间为(-∞,- ),( ,+∞);
单调增区间为(- , ).所以f(x)的极大值为f( ),极小
值为f(- ),故②正确.因为x>2和x<0时,f(x)<0恒成立.
所以f(x)无最小值,但有最大值f( ),
所以③不正确,④正确.故选A.【题型示范】
类型一 求函数的最值
【典例1】(1)函数f(x)=lnx-x在区间(0,e]上的最大值为
( )
A.1-e B.-1 C.-e D.0
(2)求f(x)=x3-3x2-9x+5在[-4,4]上的最大值和最小值.【解题探究】1.题(1)中f′(x)在(0,e]内的符号是什么?
2.题(2)中求闭区间上函数最大最小值的关键是什么?
【探究提示】1.在(0,1)时,f′(x)>0,在(1,e)时,f′(x)<0.
2.关键是要找到函数f(x)在[-4,4]内的极值与端点值.【自主解答】(1)选B.f′(x)=
当x∈(0,1)时,f′(x)>0,当x∈(1,e)时,f′(x)<0,
所以f(x)在(0,1)上递增,在(1,e)上递减,
故当x=1时,f(x)取得极大值,也为最大值,f(1)=-1.故选B.(2)f′(x)=3x2-6x-9=3(x+1)(x-3),
令f′(x)=0得x1=-1,x2=3,
所以f(x)在x=-1处有极大值f(-1)=10,
f(x)在x=3处有极小值f(3)=-22,
在区间端点处f(-4)=-71,f(4)=-15,
比较上述结果得,f(x)在[-4,4]上的最大值为f(-1)=10,最小值为f(-4)=-71.【方法技巧】求函数最值的四个步骤
第一步求函数的定义域.
第二步求f′(x),解方程f′(x)=0.
第三步列出关于x,f(x),f′(x)的变化表.
第四步求极值、端点值,确定最值.【变式训练】已知函数f(x)=x2-cos x,x∈[ ]的值域是_______.
【解析】因为f(-x)=(-x)2-cos(-x)=x2-cos x=f(x),
所以函数为偶函数.
求导函数,可得f′(x)=2x+sin x,
当x∈[0, ]时,f′(x)>0,函数为单调增函数,
因为f(0)=0-1=-1,f( )=
所以函数f(x)=x2-cos x,x∈[0, ]的值域是[-1, ],
所以函数f(x)=x2-cos x,x∈[- , ]的值域是[-1, ].
答案:[-1, ]【补偿训练】已知函数f(x)=x3+ax2+b的图象在点P(1,0)处的切线与直线3x+y=0平行.
(1)求常数a,b的值.
(2)求函数f(x)在区间[0,m]上的最小值和最大值(m>0).【解析】(1)f′(x)=3x2+2ax,
f′(1)=3+2a=-3,所以a=-3,
f(1)=a+b+1=0,所以b=2.
(2)f(x)=x3-3x2+2,f′(x)=3x2-6x,
令f′(x)=0得,x1=0,x2=2,当x<0或x>2时,f′(x)>0,当0所以f(x)的增区间为(-∞,0)和(2,+∞),减区间为(0,2),
f(0)=2,令f(x)=x3-3x2+2=2得x=0或x=3.
所以f(0)=f(3)=2,①当0f(x)max=f(0)=2;
②当2③当m>3时,f(x)min=f(2)=-2,
f(x)max=f(m)=m3-3m2+2.类型二 由函数的最值求参数的值(范围)
【典例2】(1)若函数f(x)=3x-x3在区间(a2-12,a)上有最小值,则实数a的取值范围是( )
A.(-1, ) B.(-1,4)
C.(-1,2] D.(-1,2)
(2)已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
①若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值.
②当a=3,b=-9时,若函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.【解题探究】1.题(1)中f(x)的极小值是什么?
2.题(2)中由在交点(1,c)处具有公切线,可以得出什么条件?
【探究提示】1.先求f(x)的导函数f′(x),然后可知当x=-1时取极小值为-2.
2.可以得(1,c)在f(x)与g(x)上且在此点处两个函数的导数值相等.【自主解答】(1)选C.由题知f′(x)=3-3x2,令f′(x)>0解得
-11,由此得函数在(-∞,-1)上是减函数,在(-1,1)上是增函数,在(1,+∞)上是减函数.故函数在x=-1处取到极小值-2,判断知此极小值必是区间(a2-12,a)上的最小值.所以a2-12<-1综上知a∈(-1,2].故选C.(2)①f′(x)=2ax,g′(x)=3x2+b,
f(1)=a+1=c,
由已知可得 g(1)=1+b=c,解得a=b=3.
2a=3+b,
②f(x)=3x2+1,g(x)=x3-9x,
h(x)=f(x)+g(x)=x3+3x2-9x+1,
h′(x)=3x2+6x-9.令h′(x)=0,得x1=-3,x2=1,
当x变化时h′(x)及h(x)的变化情况如下表.当x=-3时,取极大值28;
当x=1时,取极小值-4.而h(2)=3如果h(x)在区间[k,2]上的最大值为28,则k≤-3.【方法技巧】
1.含参数的函数最值问题的两类情况
(1)能根据条件确定出参数,从而化为不含参数函数的最值问题.
(2)不能求出参数时,常需分类讨论.若参数对导数的正负有影响时,需讨论参数;若极值与函数端点值比较大小不能确定,也需分类讨论以确定最值.
2.已知函数最值求参数值(范围)的思路
已知函数在某区间上的最值求参数的值(范围)是求函数最值的逆向思维,一般先求导数,利用导数研究函数的单调性及极值点,探索最值点,根据已知最值列方程(不等式)解决问题.【变式训练】已知函数
f(x)=(4x2+4ax+a2) ,其中a<0.
(1)当a=-4时,求f(x)的单调递增区间.
(2)若f(x)在区间[1,4]上的最小值为8,求a的值.【解析】(1)当a=-4时,f(x)=(4x2-16x+16) ,定义域为
[0,+∞),f′(x)=(8x-16)
令f′(x)>0得02,所以f(x)的单
调递增区间为 ,[2,+∞).
(2)f′(x)=
令f′(x)=0得x= 或x=
f(x)在定义域上的单调性为 上增, 上减,
上增.
从而需要讨论 与1及4的大小.①当 ≥4或 ≤1,即a≤-40或-2≤a<0时,f(x)在
[1,4]上增,故f(x)的最小值为f(1)=4+4a+a2=8,
解得a=-2± ,均舍去;
②当 ≤1且 ≥4,
即-10≤a≤-8时,f(x)在[1,4]上减,
故f(x)的最小值为f(4)=2(64+16a+a2)=8,
解得a=-10或a=-6(舍去);③当1< <4,即-8因为 =0,所以不成立;
④当1< <4,即-40 上减,f(x)的最小值为f(1)与f(4)中的一个,
根据上面的①②得均不成立.综上所述a=-10.【补偿训练】函数f(x)=xa-ax(0A.1 B. C.0 D.a
【解题指南】先求出函数f(x)的导数,再求出其极值点,因为在区间[0,+∞)内是惟一的极值点,也即最大值点.【解析】选A.因为f(x)=xa-ax,所以f′(x)=axa-1-a=a(xa-1-1)(0当00;当x>1时,f′(x)<0.所以当x=1时,函数f(x)=xa-ax(0故函数f(x)=xa-ax(0【典例3】(1)函数f(x)=x3-3x-1,若对于区间[-3,2]上的任意x1,x2都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )
A.20 B.18 C.1 D.0
(2)已知函数f(x)=ekx-2x(k为非零常数).
①当k=1时,求函数f(x)的最小值.
②若f(x)≥1恒成立,求k的值.【解题探究】1.题(1)中|f(x1)-f(x2)|≤t等价于什么?
2.题(2)中①要求最小值先求什么?
【探究提示】1.对于区间[-3,2]上的任意x1,x2都有|f(x1)-f(x2)|≤t,等价于对于区间[-3,2]上的任意x,都有f(x)max-f(x)min≤t,利用导数确定函数的单调性,求最值,即可得出结论.
2.将k=1代入函数f(x),应先求出导函数f′(x)=0的根,确定出函数的极小值即最小值.【自主解答】(1)选A.对于区间[-3,2]上的任意x1,x2都有|f(x1)-f(x2)|≤t,等价于对于区间[-3,2]上的任意x,都有f(x)max-f(x)min≤t,
因为f(x)=x3-3x-1,所以f′(x)=3x2-3=3(x-1)(x+1),
因为x∈[-3,2],所以函数在[-3,-1],[1,2]上单调递增,在[-1,1]上单调递减,
所以f(x)max=f(2)=f(-1)=1,f(x)min=f(-3)=-19.
所以f(x)max-f(x)min=20,所以t≥20,
所以实数t的最小值是20,故选A.(2)①因为f(x)=ex-2x,所以f′(x)=ex-2,
令f′(x)=0,得x=ln2,所以当xln2时,f′(x)>0,可得f(x)在(ln2,+∞)上单调递增,
所以f(x)的最小值为f(ln2)=2-2ln2.
②因为f′(x)=kekx-2,
(ⅰ)当k<0时,f′(x)恒小于零,则f(x)在R上单调递减;
因为当x>0时,f(x)所以不符合f(x)≥1恒成立.(ⅱ)当k>0时,令f′(x)=0,得
当x< 时,f′(x)<0,可知f(x)在(-∞, )上单调递减,
当x> 时,f′(x)>0,可知f(x)在( ,+∞)上单调递增,
所以f(x)的最小值为f( )=
因为f(x)≥1恒成立,即f(x)min≥1恒成立,
所以 ≥1,构造函数g(x)=x-xln x(x>0),则有g( )≥1,
因为g′(x)=1-ln x-1=-ln x,
所以g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以g(x)≤g(1)=1,当且仅当x=1时取得最大值,
结合g( )≥1,所以 =1,所以k=2.【延伸探究】若将题(1)中的“任意x1,x2都有|f(x1)-f(x2)|≤t”改为“任意x都有f(x)≤t”结果如何?
【解析】选C.对于区间[-3,2]上的任意x都有f(x)≤t,等价于对于区间[-3,2]上的任意x,都有f(x)max≤t,
因为f(x)=x3-3x-1,所以f′(x)=3x2-3=3(x-1)(x+1),
因为x∈[-3,2],所以函数在[-3,-1],[1,2]上单调递增,在[-1,1]上单调递减,
所以f(x)max=f(2)=f(-1)=1,所以t≥1.【方法技巧】分离参数求解不等式恒成立问题【变式训练】已知函数f(x)=ax+lnx,x∈[1,e].
(1)若a=1,求f(x)的最大值.
(2)若f(x)≤0恒成立,求a的取值范围.
【解析】(1)若a=1,则f(x)=x+lnx,f′(x)=
因为x∈[1,e],所以f′(x)>0,
所以f(x)在[1,e]上为增函数,
所以f(x)max=f(e)=e+1.(2)要使x∈[1,e],f(x)≤0恒成立,只需x∈[1,e]时,
f(x)max≤0,
显然当a≥0时,f(x)=ax+ln x在[1,e]上单增,
所以f(x)max=f(e)=ae+1>0,不合题意;
当a<0时,f′(x)=
令f′(x)=0,x=
当x< 时,f′(x)>0,当x> 时,f′(x)<0,①当 ≤1,即a≤-1时,f(x)在[1,e]上为减函数,
所以f(x)max=f(1)=a<0,
所以a≤-1;
②当 ≥e,即 ≤a<0时,f(x)在[1,e]上为增函数,
所以f(x)max=f(e)=ae+1≤0,a≤ ,所以a= ;
③当1<所以f(x)max=f( )=-1+ln( ).因为1< 所以f( )<0成立;
由①②③可得a≤ .【补偿训练】设f(x)=lnx,g(x)=f(x)+f′(x).
(1)求g(x)的单调区间和最小值.
(2)求a的取值范围,使得g(a)-g(x)< 对任意x>0成立.
【解题指南】(1)先求函数f(x)的导数,得到函数g(x)的解析式,再利用导数求函数g(x)的单调区间和最小值.
(2)要使g(a)-g(x)< 恒成立,等价于g(a)-g(x)min< 成立.【解析】(1)由题设知f′(x)= ,g(x)=
所以g′(x)= .令g′(x)=0得x=1.
当x∈(0,1)时,g′(x)<0,故(0,1)是g(x)的单调递减区间;
当x∈(1,+∞)时,g′(x)>0,故(1,+∞)是g(x)的单调递增区间.因此,x=1是g(x)在(0,+∞)上的惟一极值点,且为极小值点,从而是最小值点,所以最小值为g(1)=1.
(2)由(1)知g(x)的最小值为1,所以,g(a)-g(x)< ,对任意x>0成立?g(a)-1< ,即ln a<1,从而得0<a<e.【误区警示】解决题(1)时,一定要注意函数自变量的取值范围.【拓展类型】与最值有关的不等式的求解或证明问题
【备选典例】(1)函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
A.(-1,1) B.(-1,+∞)
C.(-∞,-1) D.(-∞,+∞)
(2)已知m∈R,函数f(x)=(x2+mx+m)ex,
①若函数没有零点,求实数m的取值范围.
②当m=0时,求证f(x)≥x2+x3.【解析】(1)选B.构造函数g(x)=f(x)-(2x+4),则g(-1)=
f(-1)-(-2+4)=2-2=0,又因为f′(x)>2,所以g′(x)=f′(x)-2>0,可知g(x)在R上是增函数,所以f(x)>2x+4可化为g(x)>0,即g(x)>g(-1),利用单调性可知,x>-1.选B.
(2)①由已知条件f(x)=0无解,即x2+mx+m=0无实根,
则Δ=m2-4m<0,解得0设g(x)=ex-x-1,所以g′(x)=ex-1,g(x),g′(x)随x变化情况如下:
由此可知对于x∈R,g(x)≥g(0),
即ex-x-1≥0,因此x2(ex-x-1)≥0,整理得,
x2ex≥x3+x2,即f(x)≥x3+x2.【方法技巧】用导数证明不等式的方法
(1)利用导数证明不等式要考虑构造新的函数,利用新函数的单调性或最值解决不等式的证明问题.比如要证明对?x∈[a,b]都有f(x)≥g(x),可设h(x)=f(x)-g(x)只要利用导数说明h(x)在[a,b]上的最小值为0即可.
(2)利用导数解决不等式,应特别注意区间端点是否取得到.
(3)学会观察不等式与函数的内在联系,构造函数再利用导数证明不等式,借助导数工具来解决不等式的证明问题,是转化与化归思想在中学数学中的重要体现.【易错误区】利用导数求函数的最值的误区
【典例】已知函数f(x)=(x2+1)(x+a)(a∈R),当f′(-1)=0时,函数y=f(x)在[ ]上的最大值为__________,最小值为__________.【解析】f(x)=x3+ax2+x+a,f′(x)=3x2+2ax+1,f′(-1)=
3-2a+1=0,所以a=2.f′(x)=3x2+4x+1=3(x+ )(x+1),
由f′(x)=3(x+1)(x+ )>0,得x<-1或x>- ;
由f′(x)=3(x+1)(x+ )<0,得-1<x<- .
所以函数的递增区间是[- ,-1],[- ,1];
函数的递减区间是[-1,- ].
f(- )= ,f(-1)=2,f(- )= ,f(1)=6,
所以函数f(x)在[ ,1]上的最大值为6,最小值为
答案:6 【常见误区】【防范措施】
求函数最值时的注意点
求函数最值时,若函数的定义域是闭区间,则需比较极值点处函数值与端点处函数值的大小;如本例中需比较极值与端点值的大小才能确定出最值.若函数的定义域是开区间且只有一个极值点,则该极值点就是最值点.【类题试解】设f(x)=x3-3x2+5,x∈[1,3],则f(x)的最大值为__________,最小值为__________.
【解析】f′(x)=3x2-6x,令f′(x)=0,得x=0或x=2.列表如下:(-∞,0)和(2,+∞)是函数f(x)的单调递增区间;(0,2)是函数f(x)的单调递减区间.
由此可知,当x∈[1,3]时,f(x)在x=2处取得极小值,无极大值.又f(1)=3,f(2)=1,f(3)=5,所以f(x)在区间[1,3]上的最大值是5,最小值是1.
答案:5 1
函数的最大(小)值与导数1.函数y=f(x)在闭区间[a,b]上取得最值的条件
如果在区间[a,b]上函数y=f(x)的图象是_____________的曲
线,那么它必有最大值和最小值.
2.求函数y=f(x)在[a,b]上的最大值与最小值的步骤
(1)求函数y=f(x)在_______内的极值.
(2)将函数y=f(x)的_______与端点处的_________________比
较,其中_____的一个是最大值,_____的一个是最小值.一条连续不断(a,b)各极值函数值f(a),f(b)最大最小1.判一判(正确的打“√”,错误的打“×”)
(1)函数的最大值一定是函数的极大值.( )
(2)开区间上的单调连续函数无最值.( )
(3)函数f(x)在区间[a,b]上的最大值和最小值一定在两个端点处取得.( )【解析】(1)错误.最大值也可能是端点的值.
(2)正确.在开区间上的单调函数无极值且端点处函数值取不到,故无最值.
(3)错误.函数f(x)在[a,b]上的最大值和最小值也有可能在区间内部某个极值点处取得.
答案:(1)× (2)√ (3)×2.做一做(请把正确的答案写在横线上)
(1)设函数f(x)=e2x+3x(x∈R),则f(x)__________(填“有”或“无”)最值.
(2)已知函数y=x3-x2-x,该函数在区间[0,3]上的最大值是__________.
(3)已知函数f(x)=-x3+3x2+m(x∈[-2,2]),f(x)的最小值为1,则m=__________.【解析】(1)因为函数f(x)=e2x+3x(x∈R),所以f′(x)=2e2x+3>0,所以函数f(x)在R上单调递增,没有最值.
答案:无
(2)y′=3x2-2x-1=(3x+1)(x-1),
当0≤x<1时,y′<0,当1
所以当x=1时,y取得极小值,即最小值,为-1,
又当x=0时,y=0,当x=3时,y=15,
所以该函数在区间[0,3]上的最大值是15.
答案:15(3)f′(x)=-3x2+6x=-3x(x-2),令f′(x)=0,解得x=0或x=2.当x∈[-2,2]时,解f′(x)<0,得-2≤x<0;解f′(x)>0,得0
知识点 函数的最大(小)值与导数
1.对函数最值的三点说明
(1)闭区间上的连续函数一定有最值,开区间内的连续函数不一定有最值.若有惟一的极值,则此极值必是函数的最值.
(2)函数的最大值和最小值是一个整体性概念.
(3)函数y=f(x)在[a,b]上连续,是函数y=f(x)在[a,b]上有最大值或最小值的充分而非必要条件.2.函数极值与最值的关系
(1)函数的极值是函数在某一点附近的局部概念,函数的最大值和最小值是一个整体性概念.
(2)函数的最大值、最小值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,函数的极值可以有多个,但最值只能有一个.
(3)极值只能在区间内取得,最值则可以在端点处取得.有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值不在端点处取得时必定是极值.【知识拓展】开区间(a,b)上连续函数y=f(x)的最值的几种情况
图(1)中的连续函数y=f(x)在开区间(a,b)上有最大值无最小值;
图(2)中的连续函数y=f(x)在开区间(a,b)上有最小值无最大值;
图(3)中的连续函数y=f(x)在开区间(a,b)上既无最大值也无最
小值;
图(4)中的连续函数y=f(x)在开区间(a,b)上既有最大值也有最
小值.【微思考】
(1)函数的极值是否一定是函数的最值?
提示:不一定.端点值也可能是函数的最值.
(2)如果在开区间(a,b)上的连续函数y=f(x)只有一个极值且为极小值,那么函数在开区间(a,b)上有最值吗?
提示:有最小值,无最大值.若x0是函数的极值点,则函数在(a,x0)是减函数,在(x0,b)是增函数,故f(x)在x=x0处取得最小值.【即时练】
关于函数f(x)=(2x-x2)ex,则下列四个结论:
①f(x)>0的解集为{x|0
③f(x)没有最小值,也没有最大值;
④f(x)没有最小值,有最大值.
其中正确结论为( )
A.①②④ B.①②③ C.①③ D.②④【解析】选A.由f(x)>0可得(2x-x2)ex>0,
因为ex>0,所以2x-x2>0,所以0
由f′(x)<0得,x> 或x<- ,
由f′(x)>0得,-
单调增区间为(- , ).所以f(x)的极大值为f( ),极小
值为f(- ),故②正确.因为x>2和x<0时,f(x)<0恒成立.
所以f(x)无最小值,但有最大值f( ),
所以③不正确,④正确.故选A.【题型示范】
类型一 求函数的最值
【典例1】(1)函数f(x)=lnx-x在区间(0,e]上的最大值为
( )
A.1-e B.-1 C.-e D.0
(2)求f(x)=x3-3x2-9x+5在[-4,4]上的最大值和最小值.【解题探究】1.题(1)中f′(x)在(0,e]内的符号是什么?
2.题(2)中求闭区间上函数最大最小值的关键是什么?
【探究提示】1.在(0,1)时,f′(x)>0,在(1,e)时,f′(x)<0.
2.关键是要找到函数f(x)在[-4,4]内的极值与端点值.【自主解答】(1)选B.f′(x)=
当x∈(0,1)时,f′(x)>0,当x∈(1,e)时,f′(x)<0,
所以f(x)在(0,1)上递增,在(1,e)上递减,
故当x=1时,f(x)取得极大值,也为最大值,f(1)=-1.故选B.(2)f′(x)=3x2-6x-9=3(x+1)(x-3),
令f′(x)=0得x1=-1,x2=3,
所以f(x)在x=-1处有极大值f(-1)=10,
f(x)在x=3处有极小值f(3)=-22,
在区间端点处f(-4)=-71,f(4)=-15,
比较上述结果得,f(x)在[-4,4]上的最大值为f(-1)=10,最小值为f(-4)=-71.【方法技巧】求函数最值的四个步骤
第一步求函数的定义域.
第二步求f′(x),解方程f′(x)=0.
第三步列出关于x,f(x),f′(x)的变化表.
第四步求极值、端点值,确定最值.【变式训练】已知函数f(x)=x2-cos x,x∈[ ]的值域是_______.
【解析】因为f(-x)=(-x)2-cos(-x)=x2-cos x=f(x),
所以函数为偶函数.
求导函数,可得f′(x)=2x+sin x,
当x∈[0, ]时,f′(x)>0,函数为单调增函数,
因为f(0)=0-1=-1,f( )=
所以函数f(x)=x2-cos x,x∈[0, ]的值域是[-1, ],
所以函数f(x)=x2-cos x,x∈[- , ]的值域是[-1, ].
答案:[-1, ]【补偿训练】已知函数f(x)=x3+ax2+b的图象在点P(1,0)处的切线与直线3x+y=0平行.
(1)求常数a,b的值.
(2)求函数f(x)在区间[0,m]上的最小值和最大值(m>0).【解析】(1)f′(x)=3x2+2ax,
f′(1)=3+2a=-3,所以a=-3,
f(1)=a+b+1=0,所以b=2.
(2)f(x)=x3-3x2+2,f′(x)=3x2-6x,
令f′(x)=0得,x1=0,x2=2,当x<0或x>2时,f′(x)>0,当0
f(0)=2,令f(x)=x3-3x2+2=2得x=0或x=3.
所以f(0)=f(3)=2,①当0
②当2
f(x)max=f(m)=m3-3m2+2.类型二 由函数的最值求参数的值(范围)
【典例2】(1)若函数f(x)=3x-x3在区间(a2-12,a)上有最小值,则实数a的取值范围是( )
A.(-1, ) B.(-1,4)
C.(-1,2] D.(-1,2)
(2)已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
①若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值.
②当a=3,b=-9时,若函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.【解题探究】1.题(1)中f(x)的极小值是什么?
2.题(2)中由在交点(1,c)处具有公切线,可以得出什么条件?
【探究提示】1.先求f(x)的导函数f′(x),然后可知当x=-1时取极小值为-2.
2.可以得(1,c)在f(x)与g(x)上且在此点处两个函数的导数值相等.【自主解答】(1)选C.由题知f′(x)=3-3x2,令f′(x)>0解得
-1
f(1)=a+1=c,
由已知可得 g(1)=1+b=c,解得a=b=3.
2a=3+b,
②f(x)=3x2+1,g(x)=x3-9x,
h(x)=f(x)+g(x)=x3+3x2-9x+1,
h′(x)=3x2+6x-9.令h′(x)=0,得x1=-3,x2=1,
当x变化时h′(x)及h(x)的变化情况如下表.当x=-3时,取极大值28;
当x=1时,取极小值-4.而h(2)=3
1.含参数的函数最值问题的两类情况
(1)能根据条件确定出参数,从而化为不含参数函数的最值问题.
(2)不能求出参数时,常需分类讨论.若参数对导数的正负有影响时,需讨论参数;若极值与函数端点值比较大小不能确定,也需分类讨论以确定最值.
2.已知函数最值求参数值(范围)的思路
已知函数在某区间上的最值求参数的值(范围)是求函数最值的逆向思维,一般先求导数,利用导数研究函数的单调性及极值点,探索最值点,根据已知最值列方程(不等式)解决问题.【变式训练】已知函数
f(x)=(4x2+4ax+a2) ,其中a<0.
(1)当a=-4时,求f(x)的单调递增区间.
(2)若f(x)在区间[1,4]上的最小值为8,求a的值.【解析】(1)当a=-4时,f(x)=(4x2-16x+16) ,定义域为
[0,+∞),f′(x)=(8x-16)
令f′(x)>0得0
调递增区间为 ,[2,+∞).
(2)f′(x)=
令f′(x)=0得x= 或x=
f(x)在定义域上的单调性为 上增, 上减,
上增.
从而需要讨论 与1及4的大小.①当 ≥4或 ≤1,即a≤-40或-2≤a<0时,f(x)在
[1,4]上增,故f(x)的最小值为f(1)=4+4a+a2=8,
解得a=-2± ,均舍去;
②当 ≤1且 ≥4,
即-10≤a≤-8时,f(x)在[1,4]上减,
故f(x)的最小值为f(4)=2(64+16a+a2)=8,
解得a=-10或a=-6(舍去);③当1< <4,即-8
④当1< <4,即-40
根据上面的①②得均不成立.综上所述a=-10.【补偿训练】函数f(x)=xa-ax(0
【解题指南】先求出函数f(x)的导数,再求出其极值点,因为在区间[0,+∞)内是惟一的极值点,也即最大值点.【解析】选A.因为f(x)=xa-ax,所以f′(x)=axa-1-a=a(xa-1-1)(0
A.20 B.18 C.1 D.0
(2)已知函数f(x)=ekx-2x(k为非零常数).
①当k=1时,求函数f(x)的最小值.
②若f(x)≥1恒成立,求k的值.【解题探究】1.题(1)中|f(x1)-f(x2)|≤t等价于什么?
2.题(2)中①要求最小值先求什么?
【探究提示】1.对于区间[-3,2]上的任意x1,x2都有|f(x1)-f(x2)|≤t,等价于对于区间[-3,2]上的任意x,都有f(x)max-f(x)min≤t,利用导数确定函数的单调性,求最值,即可得出结论.
2.将k=1代入函数f(x),应先求出导函数f′(x)=0的根,确定出函数的极小值即最小值.【自主解答】(1)选A.对于区间[-3,2]上的任意x1,x2都有|f(x1)-f(x2)|≤t,等价于对于区间[-3,2]上的任意x,都有f(x)max-f(x)min≤t,
因为f(x)=x3-3x-1,所以f′(x)=3x2-3=3(x-1)(x+1),
因为x∈[-3,2],所以函数在[-3,-1],[1,2]上单调递增,在[-1,1]上单调递减,
所以f(x)max=f(2)=f(-1)=1,f(x)min=f(-3)=-19.
所以f(x)max-f(x)min=20,所以t≥20,
所以实数t的最小值是20,故选A.(2)①因为f(x)=ex-2x,所以f′(x)=ex-2,
令f′(x)=0,得x=ln2,所以当x
所以f(x)的最小值为f(ln2)=2-2ln2.
②因为f′(x)=kekx-2,
(ⅰ)当k<0时,f′(x)恒小于零,则f(x)在R上单调递减;
因为当x>0时,f(x)
当x< 时,f′(x)<0,可知f(x)在(-∞, )上单调递减,
当x> 时,f′(x)>0,可知f(x)在( ,+∞)上单调递增,
所以f(x)的最小值为f( )=
因为f(x)≥1恒成立,即f(x)min≥1恒成立,
所以 ≥1,构造函数g(x)=x-xln x(x>0),则有g( )≥1,
因为g′(x)=1-ln x-1=-ln x,
所以g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以g(x)≤g(1)=1,当且仅当x=1时取得最大值,
结合g( )≥1,所以 =1,所以k=2.【延伸探究】若将题(1)中的“任意x1,x2都有|f(x1)-f(x2)|≤t”改为“任意x都有f(x)≤t”结果如何?
【解析】选C.对于区间[-3,2]上的任意x都有f(x)≤t,等价于对于区间[-3,2]上的任意x,都有f(x)max≤t,
因为f(x)=x3-3x-1,所以f′(x)=3x2-3=3(x-1)(x+1),
因为x∈[-3,2],所以函数在[-3,-1],[1,2]上单调递增,在[-1,1]上单调递减,
所以f(x)max=f(2)=f(-1)=1,所以t≥1.【方法技巧】分离参数求解不等式恒成立问题【变式训练】已知函数f(x)=ax+lnx,x∈[1,e].
(1)若a=1,求f(x)的最大值.
(2)若f(x)≤0恒成立,求a的取值范围.
【解析】(1)若a=1,则f(x)=x+lnx,f′(x)=
因为x∈[1,e],所以f′(x)>0,
所以f(x)在[1,e]上为增函数,
所以f(x)max=f(e)=e+1.(2)要使x∈[1,e],f(x)≤0恒成立,只需x∈[1,e]时,
f(x)max≤0,
显然当a≥0时,f(x)=ax+ln x在[1,e]上单增,
所以f(x)max=f(e)=ae+1>0,不合题意;
当a<0时,f′(x)=
令f′(x)=0,x=
当x< 时,f′(x)>0,当x> 时,f′(x)<0,①当 ≤1,即a≤-1时,f(x)在[1,e]上为减函数,
所以f(x)max=f(1)=a<0,
所以a≤-1;
②当 ≥e,即 ≤a<0时,f(x)在[1,e]上为增函数,
所以f(x)max=f(e)=ae+1≤0,a≤ ,所以a= ;
③当1<
由①②③可得a≤ .【补偿训练】设f(x)=lnx,g(x)=f(x)+f′(x).
(1)求g(x)的单调区间和最小值.
(2)求a的取值范围,使得g(a)-g(x)< 对任意x>0成立.
【解题指南】(1)先求函数f(x)的导数,得到函数g(x)的解析式,再利用导数求函数g(x)的单调区间和最小值.
(2)要使g(a)-g(x)< 恒成立,等价于g(a)-g(x)min< 成立.【解析】(1)由题设知f′(x)= ,g(x)=
所以g′(x)= .令g′(x)=0得x=1.
当x∈(0,1)时,g′(x)<0,故(0,1)是g(x)的单调递减区间;
当x∈(1,+∞)时,g′(x)>0,故(1,+∞)是g(x)的单调递增区间.因此,x=1是g(x)在(0,+∞)上的惟一极值点,且为极小值点,从而是最小值点,所以最小值为g(1)=1.
(2)由(1)知g(x)的最小值为1,所以,g(a)-g(x)< ,对任意x>0成立?g(a)-1< ,即ln a<1,从而得0<a<e.【误区警示】解决题(1)时,一定要注意函数自变量的取值范围.【拓展类型】与最值有关的不等式的求解或证明问题
【备选典例】(1)函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
A.(-1,1) B.(-1,+∞)
C.(-∞,-1) D.(-∞,+∞)
(2)已知m∈R,函数f(x)=(x2+mx+m)ex,
①若函数没有零点,求实数m的取值范围.
②当m=0时,求证f(x)≥x2+x3.【解析】(1)选B.构造函数g(x)=f(x)-(2x+4),则g(-1)=
f(-1)-(-2+4)=2-2=0,又因为f′(x)>2,所以g′(x)=f′(x)-2>0,可知g(x)在R上是增函数,所以f(x)>2x+4可化为g(x)>0,即g(x)>g(-1),利用单调性可知,x>-1.选B.
(2)①由已知条件f(x)=0无解,即x2+mx+m=0无实根,
则Δ=m2-4m<0,解得0
由此可知对于x∈R,g(x)≥g(0),
即ex-x-1≥0,因此x2(ex-x-1)≥0,整理得,
x2ex≥x3+x2,即f(x)≥x3+x2.【方法技巧】用导数证明不等式的方法
(1)利用导数证明不等式要考虑构造新的函数,利用新函数的单调性或最值解决不等式的证明问题.比如要证明对?x∈[a,b]都有f(x)≥g(x),可设h(x)=f(x)-g(x)只要利用导数说明h(x)在[a,b]上的最小值为0即可.
(2)利用导数解决不等式,应特别注意区间端点是否取得到.
(3)学会观察不等式与函数的内在联系,构造函数再利用导数证明不等式,借助导数工具来解决不等式的证明问题,是转化与化归思想在中学数学中的重要体现.【易错误区】利用导数求函数的最值的误区
【典例】已知函数f(x)=(x2+1)(x+a)(a∈R),当f′(-1)=0时,函数y=f(x)在[ ]上的最大值为__________,最小值为__________.【解析】f(x)=x3+ax2+x+a,f′(x)=3x2+2ax+1,f′(-1)=
3-2a+1=0,所以a=2.f′(x)=3x2+4x+1=3(x+ )(x+1),
由f′(x)=3(x+1)(x+ )>0,得x<-1或x>- ;
由f′(x)=3(x+1)(x+ )<0,得-1<x<- .
所以函数的递增区间是[- ,-1],[- ,1];
函数的递减区间是[-1,- ].
f(- )= ,f(-1)=2,f(- )= ,f(1)=6,
所以函数f(x)在[ ,1]上的最大值为6,最小值为
答案:6 【常见误区】【防范措施】
求函数最值时的注意点
求函数最值时,若函数的定义域是闭区间,则需比较极值点处函数值与端点处函数值的大小;如本例中需比较极值与端点值的大小才能确定出最值.若函数的定义域是开区间且只有一个极值点,则该极值点就是最值点.【类题试解】设f(x)=x3-3x2+5,x∈[1,3],则f(x)的最大值为__________,最小值为__________.
【解析】f′(x)=3x2-6x,令f′(x)=0,得x=0或x=2.列表如下:(-∞,0)和(2,+∞)是函数f(x)的单调递增区间;(0,2)是函数f(x)的单调递减区间.
由此可知,当x∈[1,3]时,f(x)在x=2处取得极小值,无极大值.又f(1)=3,f(2)=1,f(3)=5,所以f(x)在区间[1,3]上的最大值是5,最小值是1.
答案:5 1
