1.3.3 函数的最大(小)值与导数 课件3
文档属性
| 名称 | 1.3.3 函数的最大(小)值与导数 课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 00:00:00 | ||
图片预览







文档简介
课件45张PPT。1.3.3 函数的最大(小)值与导数 自主学习 新知突破1.借助函数图象,直观地理解函数的最大值和最小值的概念.
2.弄清函数最大值、最小值与极大值、极小值的区别与联系,理解和熟悉函数f(x)必有最大值和最小值的充分条件.
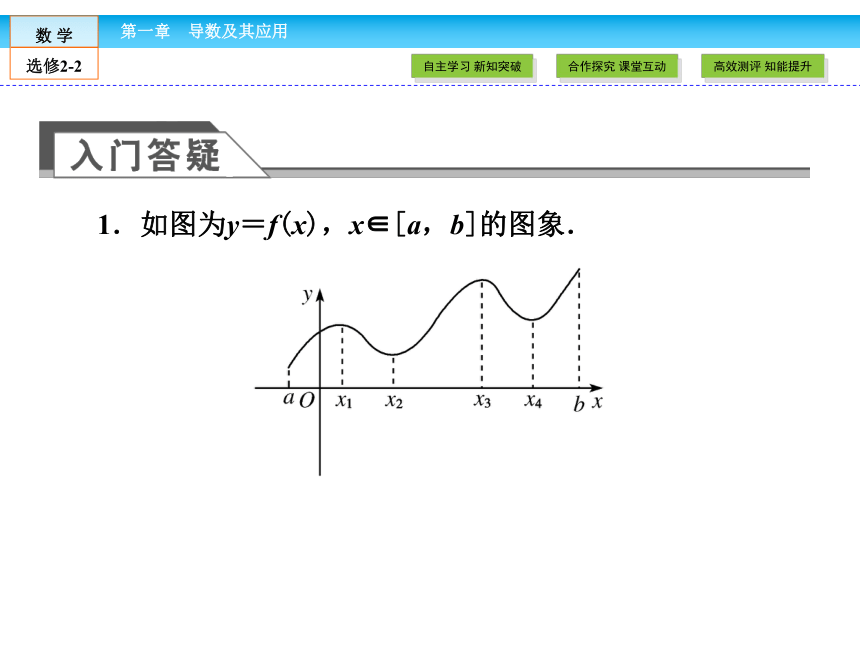
3.会用导数求在给定区间上函数的最大值、最小值.1.如图为y=f(x),x∈[a,b]的图象.
[问题1] 试说明y=f(x)的极值.
[提示1] f(x1),f(x3)为函数的极大值,f(x2),f(x4)为函数的极小值.
[问题2] 你能说出y=f(x),x∈[a,b]的最值吗?
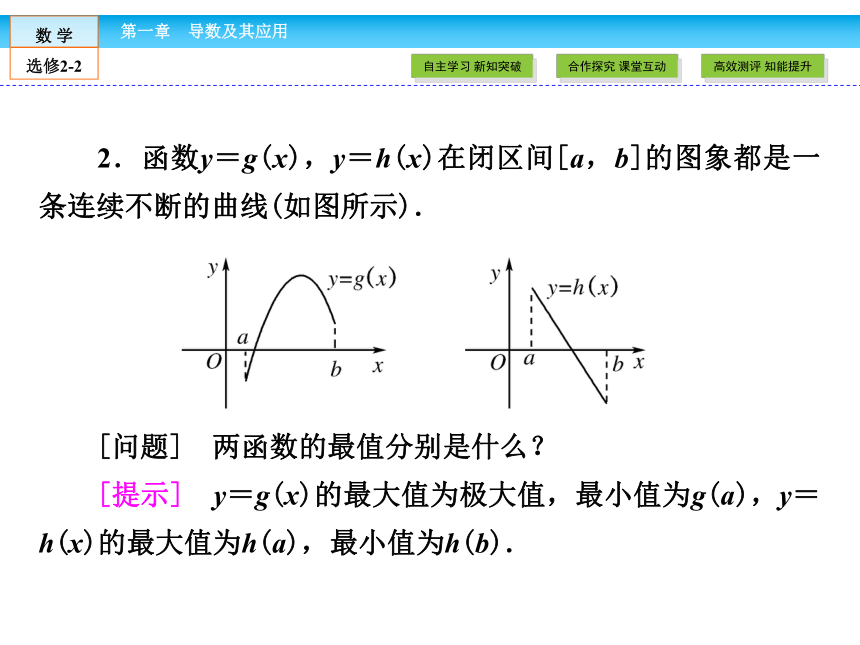
[提示2] 函数的最小值是f(a),f(x2),f(x4)中最小的,函数的最大值是f(b),f(x1),f(x3)中最大的.2.函数y=g(x),y=h(x)在闭区间[a,b]的图象都是一条连续不断的曲线(如图所示).
[问题] 两函数的最值分别是什么?
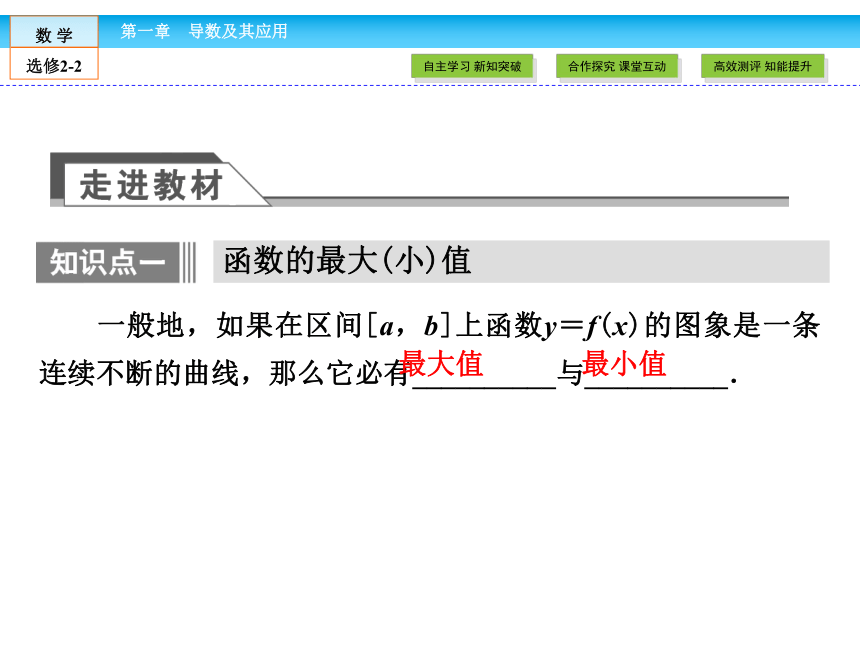
[提示] y=g(x)的最大值为极大值,最小值为g(a),y=h(x)的最大值为h(a),最小值为h(b).一般地,如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有__________与__________.函数的最大(小)值 最大值最小值
1.函数最值的理解
(1)函数的最值是一个整体性的概念.函数极值是在局部上对函数值的比较,具有相对性;而函数的最值则是表示函数在整个定义域上的情况,是对整个区间上的函数值的比较.
(2)函数在一个闭区间上若存在最大值或最小值,则最大值或最小值只能各有一个,具有唯一性,而极大值和极小值可能多于一个,也可能没有,例如:常数函数就既没有极大值也没有极小值.
(3)极值只能在区间内取得,最值则可以在端点处取得,有极值的不一定有最值,有最值的也未必有极值;极值有可能成为最值,最值只要不在端点处取必定是极值.1.求函数y=f(x)在(a,b)内的__________;
2.将函数y=f(x)的__________与_______处的函数值f(a),f(b)比较,其中最大的一个就是__________,最小的一个就是__________.求函数f(x)在闭区间[a,b]上的最值的步骤: 极值各极值端点最大值最小值
2.求函数最值需注意的问题
(1)求函数的最值,显然求极值是关键的一环.但仅仅是求最值,可用下面简化的方法求得.
①求出导数为零的点.
②比较这些点与端点处函数值的大小,就可求出函数的最大值和最小值.
(2)若函数在闭区间[a,b]上连续单调,则最大、最小值在端点处取得.
(3)若连续函数f(x)在开区间(a,b)内只有一个极值点时,这个点的函数值必然是最值.例如在(-∞,+∞)上函数只有一个极值,那么这个极值也就是最值.
1.函数f(x)=4x-x4在x∈[-1,2]上的最大值、最小值分别是( )
A.f(1)与f(-1) B.f(1)与f(2)
C.f(-1)与f(2) D.f(2)与f(-1)
解析: f′(x)=4-4x3,f′(x)>0,
即4-4x3>0?x<1,f′(x)<0?x>1,
∴f(x)=4x-x4在x=1时取得极大值,
且f(1)=3,而f(-1)=-5,f(2)=-8,
∴f(x)=4x-x4在[-1,2]上的最大值为f(1),最小值为f(2),故选B.
答案: B
2.函数f(x)=2x-cos x在(-∞,+∞)上( )
A.无最值 B.有极值
C.有最大值 D.有最小值
解析: f′(x)=2+sin x>0恒成立,所以f(x)在(-∞,+∞)上单调递增,无极值,也无最值.
答案: A合作探究 课堂互动 求函数的最值 求下列函数的最值.
[思路点拨] 要求区间[a,b]上函数的最值,只需求出函数在(a,b)内的极值,最后与端点处函数值比较大小即可. (1)f(x)=2x3-12x, 导数法求函数最值要注意的问题:
(1)求f′(x),令f′(x)=0,求出在(a,b)内使导数为0的点,同时还要找出导数不存在的点.
(2)比较三类点处的函数值:导数不存在的点,导数为0的点及区间端点的函数值,其中最大者便是f(x)在[a,b]上的最大值,最小者便是f(x)在[a,b]上的最小值.
特别提醒:比较极值与端点函数值的大小时,可以作差、作商或分类讨论. 1.求下列各函数的最值.
(1)f(x)=-x4+2x2+3,x∈[-3,2];
(2)f(x)=x3-3x2+6x-2,x∈[-1,1].
解析: (1)f′(x)=-4x3+4x,
令f′(x)=-4x(x+1)(x-1)=0得
x=-1,或x=0,或x=1.当x变化时,f′(x)及f(x)的变化情况如下表:
∴当x=-3时,f(x)取最小值-60;
当x=-1或x=1时,f(x)取最大值4.
(2)f′(x)=3x2-6x+6=3(x2-2x+2)=3(x-1)2+3,
∵f′(x)在[-1,1]内恒大于0,
∴f(x)在[-1,1]上为增函数.
故x=-1时,f(x)最小值=-12;
x=1时,f(x)最大值=2.
即f(x)的最小值为-12,最大值为2.已知函数的最值求参数 解决由函数的最值来确定参数问题的关键是利用函数的单调性确定某些极值就是函数的最值,同时由于系数a的符号对函数的单调性有直接的影响,其最值也受a的符号的影响,因此,需要进行分类讨论.本题是运用最值的定义,从逆向出发,由已知向未知转化,通过待定系数法,布列相应的方程,从而得出参数的值. 2.已知函数f(x)=ax3-6ax2+b在[-1,2]上有最大值3,最小值-29,求a,b的值.
解析: 依题意,显然a≠0.
因为f′(x)=3ax2-12ax=3ax(x-4),x∈[-1,2],
所以令f′(x)=0,解得x1=0,x2=4(舍去).(1)若a>0,当x变化时,f′(x),f(x)的变化情况如下表:
由上表知,当x=0时,f(x)取得最大值,所以f(0)=b=3.
又f(2)=-16a+3,f(-1)=-7a+3,故f(-1)>f(2),
所以当x=2时,f(x)取得最小值,即-16a+3=-29,a=2.与最值有关的恒成立问题 已知函数f(x)=ax4ln x+bx4-c(x>0)在x=1处取得极值-3-c,其中a,b,c为常数.若对任意x>0,不等式f(x)≥-2c2恒成立,求c的取值范围.
[思路点拨] 有关恒成立问题,一般是转化为求函数的最值问题.求解时要确定这个函数,看哪一个变量的范围已知,即函数是以已知范围的变量为自变量的函数.
一般地,λ≥f(x)恒成立?λ≥[f(x)]max;
λ≤f(x)恒成立?λ≤[f(x)]min. 3.已知函数f(x)=x3-3x2-9x+c,当x∈[-2,6]时,f(x)<2|c|恒成立,求c的取值范围.
解析: f(x)=x3-3x2-9x+c,
f′(x)=3x2-6x-9.
当x变化时,f′(x),f(x)随x的变化如下表:
而f(-2)=c-2,f(6)=c+54,
∴当x∈[-2,6]时,f(x)的最大值为c+54,
要使f(x)<2|c|恒成立,只要c+54<2|c|即可,
当c≥0时,c+54<2c,∴c>54;
当c<0时,c+54<-2c,∴c<-18.
∴c∈(-∞,-18)∪(54,+∞),此即为参数c的取值范围.◎求函数f(x)=x3-3x2-9x+5,x∈[-5,6]的最大值和最小值.
【错解】 f′(x)=3x2-6x-9.令f′(x)=3x2-6x-9=0,解得x=-1或x=3.
当x变化时,f′(x)与f(x)的变化情况如下表:
从上表可知,函数f(x)的最大值为10,最小值为-22.【错因】 错解的原因在于忽视闭区间端点的函数值.将f(x)的各极值与函数端点值f(a),f(b)比较,其中最大的一个就是最大值,最小的一个就是最小值.如果仅仅是求最值,还可将上面的办法简化,只需将所有可能为极值点的函数值与端点函数值进行比较,最大的即为最大值,最小的即为最小值.函数f(x)在闭区间上一定存在最大值与最小值,且一定不要忽略端点的函数值.
【正解】 由f(x)的定义域为闭区间[-5,6],而f(-5)=-150,f(6)=59,与函数的极值比较,可知函数f(x)的最大值为59,最小值为-150.高效测评 知能提升 完成练习册作业谢谢观看!
2.弄清函数最大值、最小值与极大值、极小值的区别与联系,理解和熟悉函数f(x)必有最大值和最小值的充分条件.
3.会用导数求在给定区间上函数的最大值、最小值.1.如图为y=f(x),x∈[a,b]的图象.
[问题1] 试说明y=f(x)的极值.
[提示1] f(x1),f(x3)为函数的极大值,f(x2),f(x4)为函数的极小值.
[问题2] 你能说出y=f(x),x∈[a,b]的最值吗?
[提示2] 函数的最小值是f(a),f(x2),f(x4)中最小的,函数的最大值是f(b),f(x1),f(x3)中最大的.2.函数y=g(x),y=h(x)在闭区间[a,b]的图象都是一条连续不断的曲线(如图所示).
[问题] 两函数的最值分别是什么?
[提示] y=g(x)的最大值为极大值,最小值为g(a),y=h(x)的最大值为h(a),最小值为h(b).一般地,如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有__________与__________.函数的最大(小)值 最大值最小值
1.函数最值的理解
(1)函数的最值是一个整体性的概念.函数极值是在局部上对函数值的比较,具有相对性;而函数的最值则是表示函数在整个定义域上的情况,是对整个区间上的函数值的比较.
(2)函数在一个闭区间上若存在最大值或最小值,则最大值或最小值只能各有一个,具有唯一性,而极大值和极小值可能多于一个,也可能没有,例如:常数函数就既没有极大值也没有极小值.
(3)极值只能在区间内取得,最值则可以在端点处取得,有极值的不一定有最值,有最值的也未必有极值;极值有可能成为最值,最值只要不在端点处取必定是极值.1.求函数y=f(x)在(a,b)内的__________;
2.将函数y=f(x)的__________与_______处的函数值f(a),f(b)比较,其中最大的一个就是__________,最小的一个就是__________.求函数f(x)在闭区间[a,b]上的最值的步骤: 极值各极值端点最大值最小值
2.求函数最值需注意的问题
(1)求函数的最值,显然求极值是关键的一环.但仅仅是求最值,可用下面简化的方法求得.
①求出导数为零的点.
②比较这些点与端点处函数值的大小,就可求出函数的最大值和最小值.
(2)若函数在闭区间[a,b]上连续单调,则最大、最小值在端点处取得.
(3)若连续函数f(x)在开区间(a,b)内只有一个极值点时,这个点的函数值必然是最值.例如在(-∞,+∞)上函数只有一个极值,那么这个极值也就是最值.
1.函数f(x)=4x-x4在x∈[-1,2]上的最大值、最小值分别是( )
A.f(1)与f(-1) B.f(1)与f(2)
C.f(-1)与f(2) D.f(2)与f(-1)
解析: f′(x)=4-4x3,f′(x)>0,
即4-4x3>0?x<1,f′(x)<0?x>1,
∴f(x)=4x-x4在x=1时取得极大值,
且f(1)=3,而f(-1)=-5,f(2)=-8,
∴f(x)=4x-x4在[-1,2]上的最大值为f(1),最小值为f(2),故选B.
答案: B
2.函数f(x)=2x-cos x在(-∞,+∞)上( )
A.无最值 B.有极值
C.有最大值 D.有最小值
解析: f′(x)=2+sin x>0恒成立,所以f(x)在(-∞,+∞)上单调递增,无极值,也无最值.
答案: A合作探究 课堂互动 求函数的最值 求下列函数的最值.
[思路点拨] 要求区间[a,b]上函数的最值,只需求出函数在(a,b)内的极值,最后与端点处函数值比较大小即可. (1)f(x)=2x3-12x, 导数法求函数最值要注意的问题:
(1)求f′(x),令f′(x)=0,求出在(a,b)内使导数为0的点,同时还要找出导数不存在的点.
(2)比较三类点处的函数值:导数不存在的点,导数为0的点及区间端点的函数值,其中最大者便是f(x)在[a,b]上的最大值,最小者便是f(x)在[a,b]上的最小值.
特别提醒:比较极值与端点函数值的大小时,可以作差、作商或分类讨论. 1.求下列各函数的最值.
(1)f(x)=-x4+2x2+3,x∈[-3,2];
(2)f(x)=x3-3x2+6x-2,x∈[-1,1].
解析: (1)f′(x)=-4x3+4x,
令f′(x)=-4x(x+1)(x-1)=0得
x=-1,或x=0,或x=1.当x变化时,f′(x)及f(x)的变化情况如下表:
∴当x=-3时,f(x)取最小值-60;
当x=-1或x=1时,f(x)取最大值4.
(2)f′(x)=3x2-6x+6=3(x2-2x+2)=3(x-1)2+3,
∵f′(x)在[-1,1]内恒大于0,
∴f(x)在[-1,1]上为增函数.
故x=-1时,f(x)最小值=-12;
x=1时,f(x)最大值=2.
即f(x)的最小值为-12,最大值为2.已知函数的最值求参数 解决由函数的最值来确定参数问题的关键是利用函数的单调性确定某些极值就是函数的最值,同时由于系数a的符号对函数的单调性有直接的影响,其最值也受a的符号的影响,因此,需要进行分类讨论.本题是运用最值的定义,从逆向出发,由已知向未知转化,通过待定系数法,布列相应的方程,从而得出参数的值. 2.已知函数f(x)=ax3-6ax2+b在[-1,2]上有最大值3,最小值-29,求a,b的值.
解析: 依题意,显然a≠0.
因为f′(x)=3ax2-12ax=3ax(x-4),x∈[-1,2],
所以令f′(x)=0,解得x1=0,x2=4(舍去).(1)若a>0,当x变化时,f′(x),f(x)的变化情况如下表:
由上表知,当x=0时,f(x)取得最大值,所以f(0)=b=3.
又f(2)=-16a+3,f(-1)=-7a+3,故f(-1)>f(2),
所以当x=2时,f(x)取得最小值,即-16a+3=-29,a=2.与最值有关的恒成立问题 已知函数f(x)=ax4ln x+bx4-c(x>0)在x=1处取得极值-3-c,其中a,b,c为常数.若对任意x>0,不等式f(x)≥-2c2恒成立,求c的取值范围.
[思路点拨] 有关恒成立问题,一般是转化为求函数的最值问题.求解时要确定这个函数,看哪一个变量的范围已知,即函数是以已知范围的变量为自变量的函数.
一般地,λ≥f(x)恒成立?λ≥[f(x)]max;
λ≤f(x)恒成立?λ≤[f(x)]min. 3.已知函数f(x)=x3-3x2-9x+c,当x∈[-2,6]时,f(x)<2|c|恒成立,求c的取值范围.
解析: f(x)=x3-3x2-9x+c,
f′(x)=3x2-6x-9.
当x变化时,f′(x),f(x)随x的变化如下表:
而f(-2)=c-2,f(6)=c+54,
∴当x∈[-2,6]时,f(x)的最大值为c+54,
要使f(x)<2|c|恒成立,只要c+54<2|c|即可,
当c≥0时,c+54<2c,∴c>54;
当c<0时,c+54<-2c,∴c<-18.
∴c∈(-∞,-18)∪(54,+∞),此即为参数c的取值范围.◎求函数f(x)=x3-3x2-9x+5,x∈[-5,6]的最大值和最小值.
【错解】 f′(x)=3x2-6x-9.令f′(x)=3x2-6x-9=0,解得x=-1或x=3.
当x变化时,f′(x)与f(x)的变化情况如下表:
从上表可知,函数f(x)的最大值为10,最小值为-22.【错因】 错解的原因在于忽视闭区间端点的函数值.将f(x)的各极值与函数端点值f(a),f(b)比较,其中最大的一个就是最大值,最小的一个就是最小值.如果仅仅是求最值,还可将上面的办法简化,只需将所有可能为极值点的函数值与端点函数值进行比较,最大的即为最大值,最小的即为最小值.函数f(x)在闭区间上一定存在最大值与最小值,且一定不要忽略端点的函数值.
【正解】 由f(x)的定义域为闭区间[-5,6],而f(-5)=-150,f(6)=59,与函数的极值比较,可知函数f(x)的最大值为59,最小值为-150.高效测评 知能提升 完成练习册作业谢谢观看!
