1.4 生活中的优化问题举例 课件2
文档属性
| 名称 | 1.4 生活中的优化问题举例 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 00:00:00 | ||
图片预览










文档简介
课件49张PPT。1.4
生活中的优化问题举例【题型示范】
类型一 几何中的最值问题
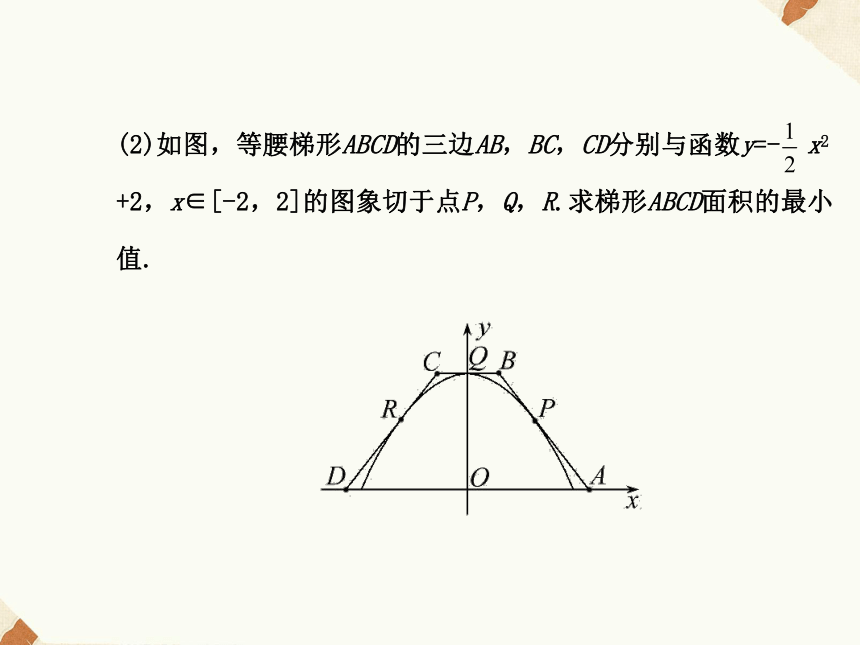
【典例1】(1)用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2∶1,则该长方体的最大体积是________m3.(2)如图,等腰梯形ABCD的三边AB,BC,CD分别与函数y=- x2
+2,x∈[-2,2]的图象切于点P,Q,R.求梯形ABCD面积的最小
值.【解题探究】1.题(1)中应设哪个未知量?如何表示其他的量?
2.题(2)中如何巧设切点坐标?在曲线上一点处的切线方程公式是什么?
【探究提示】1.根据题意知,长方体的所有棱长和是18m,故可设出宽,用宽表示出长和高,将体积表示成宽的函数,用导数来求其最大值即可.
2.可设点P的坐标为(t,- t2+2)(02x m,高是 则该长方体的体积V(x)=x·2x·( -3x)=-6x3+9x2,由V′(x)=0,得到x=1,且当0<x<1时,V′(x)>0;当1<x< 时,V′(x)<0,即体积函数V(x)在x=1处取得极大值V(1)=3,也是函数V(x)在定义域上的最大值.
所以该长方体体积最大值是3 m3.
答案:3(2)设梯形ABCD的面积为S,点P的坐标为(t,- t2+2)(0由题意得,点Q的坐标为(0,2),直线BC的方程为y=2.因为
y=- x2+2,所以y′=-x,所以y′|x=t=-t,
所以直线AB的方程为y-(- t2+2)=-t(x-t),
即:y=-tx+ t2+2,令y=0得,
所以A( ,0).
令y=2得,x= t,所以B( t,2),
所以令S′=0得t= .故当t= 时,S有最小值为
所以梯形ABCD的面积的最小值为【方法技巧】
1.解决面积、体积最值问题的思路
解决面积、体积的最值问题,要正确引入变量,将面积或体积表示为变量的函数,结合实际问题的定义域,利用导数求解函数的最值.
2.利用导数解决优化问题的基本思路3.解决优化问题时应注意的问题
(1)列函数关系式时,注意实际问题中变量的取值范围,即函数的定义域.
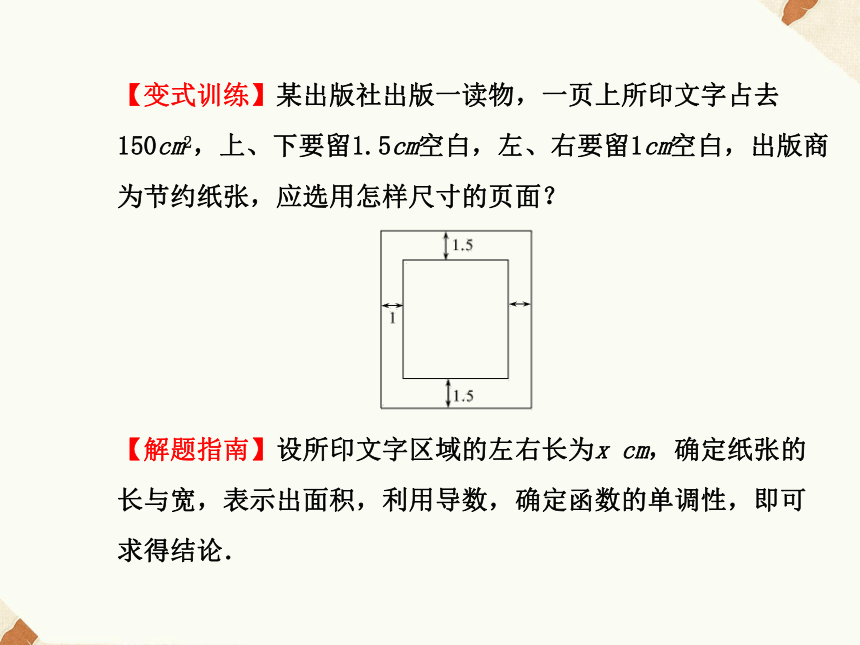
(2)一般地,通过函数的极值来求得函数的最值.如果函数f(x)在给定区间内只有一个极值点或函数f(x)在开区间上只有一个点使f′(x)=0,则只要根据实际意义判断该值是最大值还是最小值即可,不必再与端点处的函数值进行比较.【变式训练】某出版社出版一读物,一页上所印文字占去150cm2,上、下要留1.5cm空白,左、右要留1cm空白,出版商为节约纸张,应选用怎样尺寸的页面?
【解题指南】设所印文字区域的左右长为x cm,确定纸张的长与宽,表示出面积,利用导数,确定函数的单调性,即可求得结论.【解析】设所印文字区域的左右长为x cm,则上下长为
cm,所以纸张的左右长为(x+2)cm,上下长为( +
3)cm,所以纸张的面积S=(x+2)( +3)=3x+ +156.所以S′= ,令S′=0解得x=10.
当x>10时,S单调递增;当0<x<10时,S单调递减.
所以当x=10时,Smin=216(cm2),此时纸张的左右长为12 cm,上下长为18 cm.
故当纸张的边长分别为12 cm,18 cm时最节约.【补偿训练】已知三棱锥S-ABC的底面是正三角形,点A在侧面SBC上的射影H是△SBC的垂心,SA=a,则此三棱锥体积的最大值是__________.
【解题指南】说明点S在底面ABC上的射影O为△ABC的垂心,三棱锥S-ABC为正三棱锥,记SO=h(hS在底面ABC上的射影O为△ABC的垂心;又△ABC为正三角形,
所以O为△ABC的中心,即三棱锥S-ABC为正三棱锥.记SO=h(h
<a),则AO= ,于是有AB= ,记三棱锥S-ABC
的体积为f(h),则f(h)= (a2-h2)h,f′(h)= (a2-3h2),
所以f(h)max=
答案:类型二 用料(费用)最省问题
【典例2】(1)圆柱形金属饮料罐的容积一定,要使生产这种金属饮料罐所用的材料最省,它的高与底面半径比为________.(2)某网球中心欲建连成片的网球场数块,用128万元购买土地10000平方米,该中心每块球场的建设面积为1000平方米,球场的总建筑面积的每平方米的平均建设费用与球场数有关,当该中心建球场x块时,每平方米的平均建设费用(单位:元)可近似地用f(x)=800(1+ ln x)来刻画.为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),该网球中心应建几个球场?【解题探究】1.题(1)中圆柱形金属饮料罐容积一定,底面半径和高有什么关系?
2.题(2)中解决用料(费用)最省问题的关键是什么?
【探究提示】1.V=πR2h,即
2.解决用料(费用)最省问题的关键是选取合适的量作为自变量,把要求解的问题表示成自变量的函数,再利用导数求出最小值.【自主解答】(1)设圆柱形饮料罐的高为h,底面半径为R,
则表面积S=2πRh+2πR2.由V=πR2h,
得h= ,则S(R)=
= +2πR2,令S′(R)=
解得R=
从而
即h=2R,因为S(R)只有一个极值,所以它是最小值,当饮料
罐的高与底面直径相等,即h∶R=2∶1时所用材料最省.
答案:2∶1(2)设建成x个球场,则1≤x≤10,每平方米的购地费用为
元,
因为每平方米的平均建设费用(单位:元)可近似地用f(x)=
800(1+ ln x)来表示,所以每平方米的综合费用为g(x)=
f(x)+ =800+160ln x+ (x>0),所以g′(x)=
(x>0),
令g′(x)=0,则x=8,当0<x<8时,g′(x)<0,当x>8时,
g′(x)>0,所以x=8时,函数取得极小值,且为最小值.
故当建成8座球场时,每平方米的综合费用最省.【延伸探究】若把题(1)中的条件改为圆柱形金属饮料罐的表面积为定值S,要使它的容积最大,它的高与底面半径的比为________.
【解题指南】先写出饮料罐的高与底面半径的关系,再把饮料罐的体积表示成底面半径的函数,利用导数求出饮料罐容积最大时满足的条件,再求高与底面半径的比.【解析】因为S=2πRh+2πR2,所以
所以V(R)=
= (S-2πR2)R= SR-πR3,
V′(R)= S-3πR2=0,得S=6πR2,
当S=6πR2时,容积最大,
此时6πR2=2πRh+2πR2.即h∶R=2∶1.
答案:2∶1【方法技巧】利用导数解决生活中优化问题的四个步骤【变式训练】统计表明:某种型号的汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为 ,x∈(0,120],且甲、乙两地相距100千米,则当汽车以多少千米/小时的速度匀速行驶时,从甲地到乙地耗油量最少.
【解题指南】根据题意求出总耗油量h(x)与速度x的关系式,再利用导函数求出h(x)的极小值判断出就是最小值即可.【解析】当速度为x千米/小时时,汽车从甲地到乙地行驶了
小时,设耗油量为h(x)升,
依题意得h(x)=
h′(x)=
令h′(x)=0,得x=80.
当x∈(0,80)时,h′(x)<0,h(x)是减函数;
当x∈(80,120)时,h′(x)>0,h(x)是增函数.所以当x=80时,h(x)取到极小值h(80)=11.25.
因为h(x)在(0,120]上只有一个极值,所以它是最小值.故当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.【补偿训练】如图,
现要在边长为100 m的正方形区域ABCD内建
一个交通“环岛”以正方形的四个顶点为
圆心,在四个角分别建半径为x m(x不小于
9)的扇形花坛,以正方形的中心为圆心建一个半径为 x2 m的圆形草地.为了保证道路畅通,岛口宽不小于60 m,绕岛行驶的路宽均不小于10 m.(1)求x的取值范围.(运算中 取1.4)
(2)若中间草地的造价为a元/m2,四个花坛的造价为 元
/m2,其余区域的造价为 元/m2,当x取何值时,可使“环
岛”的整体造价最低? x≥9,
【解析】(1)由题意得, 100-2x≥60,
100 -2x-2× x2≥2×10,
x≥9,
解得 x≤20, 即9≤x≤15.
-20≤x≤15,(2)记“环岛”的整体造价为y元,则由题意得
令f(x)=
则f′(x)=
由f′(x)=0,解得x=0或x=10或x=15,
列表如下:所以当x=10时,y取最小值.
答:当x=10时,可使“环岛”的整体造价最低.类型三 利润最大(成本最低)问题
【典例3】(1)甲乙两地相距240 km,汽车从甲地以速度v(km/h)匀速行驶到乙地.已知汽车每小时的运输成本由固定成本和可变成本组成,固定成本为160元,可变成本为 元.为使全程运输成本最小,汽车应以_______速度行驶.(2)某工厂生产某种产品,已知该产品的月生产量x(吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24 200- x2,且生产x吨的成本为R=50 000+200x(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?【解题探究】1.题(1)中汽车每小时的运输成本由哪些成本组成?如何利用导数求最值?
2.题(2)中利润、收入、成本三者之间有何关系?求利润最大的解题思路是什么?
【探究提示】1.根据汽车每小时的运输成本由固定成本和可变成本组成,固定成本为160元,可变成本为 元,可构建函数,利用导数可求函数的极值,极值就是最值.
2.利润、收入、成本三者之间的关系为:利润=收入-成本.首先列出利润关于月生产量的关系式,再利用导数求函数的最值.【自主解答】(1)设全程运输成本为y元,由题意,得
令y′=0,得v=80.当v>80时,y′>0;
当0<v<80时,y′<0.所以v=80时,ymin=720.
答案:80 km/h(2)每月生产x吨时的利润为
f(x)=(24 200- x2)x-(50 000+200x)
=- x3+24 000x-50 000(x≥0),
由f′(x)=- x2+24 000=0,解得:x=200或x=-200(舍去).
因f(x)在[0,+∞)内只有一个点x=200使f′(x)=0,故它就是最大值点,且最大值为f(200)=- ×2003+24 000×200-
50 000=3 150 000(元),
故每月生产200吨产品时利润达到最大,最大利润为315万元.【方法技巧】
1.经济生活中优化问题的解法
经济生活中要分析生产的成本与利润及利润增减的快慢,以产量或单价为自变量很容易建立函数关系,从而可以利用导数来分析、研究、指导生产活动.
2.关于利润问题常用的两个等量关系
(1)利润=收入-成本.
(2)利润=每件产品的利润×销售件数.【变式训练】在一定面积的水域中养殖某种鱼类,每个网箱的产量p是网箱个数x的一次函数,如果放置4个网箱,则每个网箱的产量为16吨;如果放置7个网箱,则每个网箱的产量为10吨,由于该水域面积限制,最多只能放置10个网箱.
(1)试问放置多少个网箱时,总产量Q最高?
(2)若鱼的市场价为m万元/吨,养殖的总成本为(5lnx+1)万元.
(i)当m=0.25时,应放置多少个网箱才能使总收益y最大?
(ii)当m≥0.25时,求使得收益y最高的所有可能的x值组成的集合.【解析】(1)设p=ax+b,由已知得 所以
所以p=-2x+24,所以Q=px=(-2x+24)x=-2(x-6)2+72(x∈N*,
x≤10),所以当x=6时,f(x)最大,即放置6个网箱时,可使总
产量达到最大.
(2)总收益为y=f(x)=(-2x2+24x)m-(5ln x+1)(x∈N*,x≤10),
(i)当m=0.25时,f(x)=(-2x2+24x)× -(5ln x+1)=- x2+6x
-5ln x-1,所以f′(x)=当1<x<5时,f′(x)>0,当5<x<10时,f′(x)<0,所以
x=5时,函数取得极大值,也是最大值.所以应放置5个网箱才
能使总收益y最大;
(ii)当m≥0.25时,f(x)=(-2x2+24x)m-(5ln x+1),
所以f′(x)=
令f′(x)=0,即-4mx2+24mx-5=0,因为m≥0.25,所以
Δ=16m(36m-5)>0,方程-4mx2+24mx-5=0的两根分别为x1=3-
,x2=3+ ,因为m≥0.25,所以x1≤1,5≤x2<
6,所以当x∈(1,x2)时,f′(x)>0,当x2<x<10时,f′(x)<0,所以x=x2时,函数取得极大值,也是最大值.
所以使得收益y最高的所有可能的x值组成的集合为{5,6}.【补偿训练】某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3(1)求a的值.
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.【解题指南】(1)根据“销售价格为5元/千克时,每日可售出该商品11千克”可知销售函数过点(5,11),将其代入可求得a的值.
(2)利润为f(x)=(每千克产品的售价-每千克产品的成本)×销售量,表示出函数解析式后,可借助导数求最值.【解析】(1)因为x=5时,y=11,所以 +10=11,所以a=2.
(2)由(1)可知,该商品每日的销售量y= +10(x-6)2,
所以商场每日销售该商品所获得的利润
f(x)=(x-3)[ +10(x-6)2]=2+10(x-3)(x-6)2,
3从而f′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)(x-6).
于是,当x变化时,f′(x),f(x)的变化情况如下表,由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点.
所以,当x=4时,函数f(x)取得最大值,且最大值等于42.
答:当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.【规范解答】导数在解决实际问题中的应用
【典例】(12分)某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)2万件.
(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式.
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(a).【点题】警误区,促提升
失分点1:若在①处不能正确求出导数为0的点,即不舍x=12则会求错,本例最多得2分.
失分点2:若审题不清忽视对②处的讨论,仅求出一组,则本例最多得5分.
失分点3:若虽然进行了讨论,但无法确定函数取得最大值的点,即未能求出③处的值,则本例最多得7分.【悟题】提措施,导方向
1.应用分类讨论思想
在解含有参数的问题时,一定要注意分类讨论.如本例中销售价x由于管理费a的变化而变化,最终会影响利润的最大值.
2.注意限制条件的挖掘
对题目中的条件要认真分析,找出一些限制条件,如本例中x的取值,对于不符合条件的x的取值,要舍去.3.注意解题的规范性
解决实际应用题时,要注意解答过程的规范性,对于分类讨论得到的结果,如本例最大利润的结果表达式,要写成分段的形式,最后一定要进行总结.【类题试解】某工厂生产某种水杯,每个水杯的原材料费、加工费分别为30元、m元(m为常数,且2≤m≤3),设每个水杯的出厂价为x元(35≤x≤41),根据市场调查,水杯的日销售量与ex(e为自然对数的底数)成反比例,已知每个水杯的出厂价为40元时,日销售量为10个.
(1)求该工厂的日利润y(元)与每个水杯的出厂价x(元)的函数关系式.
(2)当每个水杯的出厂价为多少元时,该工厂的日利润最大,并求日利润的最大值.【解析】(1)设日销量为s,则s= ,因为x=40时,s=10,所以
10= ,所以k=10e40,所以s= .所以y= (x-30-
m)(35≤x≤41).
(2)y′= (31+m-x),令y′=0,可得x=31+m,所以当
2≤m≤3时,33≤31+m≤34,所以当35≤x≤41时,y′<0,函
数为减函数.所以当x=35时,y取最大值,最大值为10(5-
m)e5.
生活中的优化问题举例【题型示范】
类型一 几何中的最值问题
【典例1】(1)用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2∶1,则该长方体的最大体积是________m3.(2)如图,等腰梯形ABCD的三边AB,BC,CD分别与函数y=- x2
+2,x∈[-2,2]的图象切于点P,Q,R.求梯形ABCD面积的最小
值.【解题探究】1.题(1)中应设哪个未知量?如何表示其他的量?
2.题(2)中如何巧设切点坐标?在曲线上一点处的切线方程公式是什么?
【探究提示】1.根据题意知,长方体的所有棱长和是18m,故可设出宽,用宽表示出长和高,将体积表示成宽的函数,用导数来求其最大值即可.
2.可设点P的坐标为(t,- t2+2)(0
所以该长方体体积最大值是3 m3.
答案:3(2)设梯形ABCD的面积为S,点P的坐标为(t,- t2+2)(0
y=- x2+2,所以y′=-x,所以y′|x=t=-t,
所以直线AB的方程为y-(- t2+2)=-t(x-t),
即:y=-tx+ t2+2,令y=0得,
所以A( ,0).
令y=2得,x= t,所以B( t,2),
所以令S′=0得t= .故当t= 时,S有最小值为
所以梯形ABCD的面积的最小值为【方法技巧】
1.解决面积、体积最值问题的思路
解决面积、体积的最值问题,要正确引入变量,将面积或体积表示为变量的函数,结合实际问题的定义域,利用导数求解函数的最值.
2.利用导数解决优化问题的基本思路3.解决优化问题时应注意的问题
(1)列函数关系式时,注意实际问题中变量的取值范围,即函数的定义域.
(2)一般地,通过函数的极值来求得函数的最值.如果函数f(x)在给定区间内只有一个极值点或函数f(x)在开区间上只有一个点使f′(x)=0,则只要根据实际意义判断该值是最大值还是最小值即可,不必再与端点处的函数值进行比较.【变式训练】某出版社出版一读物,一页上所印文字占去150cm2,上、下要留1.5cm空白,左、右要留1cm空白,出版商为节约纸张,应选用怎样尺寸的页面?
【解题指南】设所印文字区域的左右长为x cm,确定纸张的长与宽,表示出面积,利用导数,确定函数的单调性,即可求得结论.【解析】设所印文字区域的左右长为x cm,则上下长为
cm,所以纸张的左右长为(x+2)cm,上下长为( +
3)cm,所以纸张的面积S=(x+2)( +3)=3x+ +156.所以S′= ,令S′=0解得x=10.
当x>10时,S单调递增;当0<x<10时,S单调递减.
所以当x=10时,Smin=216(cm2),此时纸张的左右长为12 cm,上下长为18 cm.
故当纸张的边长分别为12 cm,18 cm时最节约.【补偿训练】已知三棱锥S-ABC的底面是正三角形,点A在侧面SBC上的射影H是△SBC的垂心,SA=a,则此三棱锥体积的最大值是__________.
【解题指南】说明点S在底面ABC上的射影O为△ABC的垂心,三棱锥S-ABC为正三棱锥,记SO=h(h
所以O为△ABC的中心,即三棱锥S-ABC为正三棱锥.记SO=h(h
<a),则AO= ,于是有AB= ,记三棱锥S-ABC
的体积为f(h),则f(h)= (a2-h2)h,f′(h)= (a2-3h2),
所以f(h)max=
答案:类型二 用料(费用)最省问题
【典例2】(1)圆柱形金属饮料罐的容积一定,要使生产这种金属饮料罐所用的材料最省,它的高与底面半径比为________.(2)某网球中心欲建连成片的网球场数块,用128万元购买土地10000平方米,该中心每块球场的建设面积为1000平方米,球场的总建筑面积的每平方米的平均建设费用与球场数有关,当该中心建球场x块时,每平方米的平均建设费用(单位:元)可近似地用f(x)=800(1+ ln x)来刻画.为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),该网球中心应建几个球场?【解题探究】1.题(1)中圆柱形金属饮料罐容积一定,底面半径和高有什么关系?
2.题(2)中解决用料(费用)最省问题的关键是什么?
【探究提示】1.V=πR2h,即
2.解决用料(费用)最省问题的关键是选取合适的量作为自变量,把要求解的问题表示成自变量的函数,再利用导数求出最小值.【自主解答】(1)设圆柱形饮料罐的高为h,底面半径为R,
则表面积S=2πRh+2πR2.由V=πR2h,
得h= ,则S(R)=
= +2πR2,令S′(R)=
解得R=
从而
即h=2R,因为S(R)只有一个极值,所以它是最小值,当饮料
罐的高与底面直径相等,即h∶R=2∶1时所用材料最省.
答案:2∶1(2)设建成x个球场,则1≤x≤10,每平方米的购地费用为
元,
因为每平方米的平均建设费用(单位:元)可近似地用f(x)=
800(1+ ln x)来表示,所以每平方米的综合费用为g(x)=
f(x)+ =800+160ln x+ (x>0),所以g′(x)=
(x>0),
令g′(x)=0,则x=8,当0<x<8时,g′(x)<0,当x>8时,
g′(x)>0,所以x=8时,函数取得极小值,且为最小值.
故当建成8座球场时,每平方米的综合费用最省.【延伸探究】若把题(1)中的条件改为圆柱形金属饮料罐的表面积为定值S,要使它的容积最大,它的高与底面半径的比为________.
【解题指南】先写出饮料罐的高与底面半径的关系,再把饮料罐的体积表示成底面半径的函数,利用导数求出饮料罐容积最大时满足的条件,再求高与底面半径的比.【解析】因为S=2πRh+2πR2,所以
所以V(R)=
= (S-2πR2)R= SR-πR3,
V′(R)= S-3πR2=0,得S=6πR2,
当S=6πR2时,容积最大,
此时6πR2=2πRh+2πR2.即h∶R=2∶1.
答案:2∶1【方法技巧】利用导数解决生活中优化问题的四个步骤【变式训练】统计表明:某种型号的汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为 ,x∈(0,120],且甲、乙两地相距100千米,则当汽车以多少千米/小时的速度匀速行驶时,从甲地到乙地耗油量最少.
【解题指南】根据题意求出总耗油量h(x)与速度x的关系式,再利用导函数求出h(x)的极小值判断出就是最小值即可.【解析】当速度为x千米/小时时,汽车从甲地到乙地行驶了
小时,设耗油量为h(x)升,
依题意得h(x)=
h′(x)=
令h′(x)=0,得x=80.
当x∈(0,80)时,h′(x)<0,h(x)是减函数;
当x∈(80,120)时,h′(x)>0,h(x)是增函数.所以当x=80时,h(x)取到极小值h(80)=11.25.
因为h(x)在(0,120]上只有一个极值,所以它是最小值.故当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.【补偿训练】如图,
现要在边长为100 m的正方形区域ABCD内建
一个交通“环岛”以正方形的四个顶点为
圆心,在四个角分别建半径为x m(x不小于
9)的扇形花坛,以正方形的中心为圆心建一个半径为 x2 m的圆形草地.为了保证道路畅通,岛口宽不小于60 m,绕岛行驶的路宽均不小于10 m.(1)求x的取值范围.(运算中 取1.4)
(2)若中间草地的造价为a元/m2,四个花坛的造价为 元
/m2,其余区域的造价为 元/m2,当x取何值时,可使“环
岛”的整体造价最低? x≥9,
【解析】(1)由题意得, 100-2x≥60,
100 -2x-2× x2≥2×10,
x≥9,
解得 x≤20, 即9≤x≤15.
-20≤x≤15,(2)记“环岛”的整体造价为y元,则由题意得
令f(x)=
则f′(x)=
由f′(x)=0,解得x=0或x=10或x=15,
列表如下:所以当x=10时,y取最小值.
答:当x=10时,可使“环岛”的整体造价最低.类型三 利润最大(成本最低)问题
【典例3】(1)甲乙两地相距240 km,汽车从甲地以速度v(km/h)匀速行驶到乙地.已知汽车每小时的运输成本由固定成本和可变成本组成,固定成本为160元,可变成本为 元.为使全程运输成本最小,汽车应以_______速度行驶.(2)某工厂生产某种产品,已知该产品的月生产量x(吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24 200- x2,且生产x吨的成本为R=50 000+200x(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?【解题探究】1.题(1)中汽车每小时的运输成本由哪些成本组成?如何利用导数求最值?
2.题(2)中利润、收入、成本三者之间有何关系?求利润最大的解题思路是什么?
【探究提示】1.根据汽车每小时的运输成本由固定成本和可变成本组成,固定成本为160元,可变成本为 元,可构建函数,利用导数可求函数的极值,极值就是最值.
2.利润、收入、成本三者之间的关系为:利润=收入-成本.首先列出利润关于月生产量的关系式,再利用导数求函数的最值.【自主解答】(1)设全程运输成本为y元,由题意,得
令y′=0,得v=80.当v>80时,y′>0;
当0<v<80时,y′<0.所以v=80时,ymin=720.
答案:80 km/h(2)每月生产x吨时的利润为
f(x)=(24 200- x2)x-(50 000+200x)
=- x3+24 000x-50 000(x≥0),
由f′(x)=- x2+24 000=0,解得:x=200或x=-200(舍去).
因f(x)在[0,+∞)内只有一个点x=200使f′(x)=0,故它就是最大值点,且最大值为f(200)=- ×2003+24 000×200-
50 000=3 150 000(元),
故每月生产200吨产品时利润达到最大,最大利润为315万元.【方法技巧】
1.经济生活中优化问题的解法
经济生活中要分析生产的成本与利润及利润增减的快慢,以产量或单价为自变量很容易建立函数关系,从而可以利用导数来分析、研究、指导生产活动.
2.关于利润问题常用的两个等量关系
(1)利润=收入-成本.
(2)利润=每件产品的利润×销售件数.【变式训练】在一定面积的水域中养殖某种鱼类,每个网箱的产量p是网箱个数x的一次函数,如果放置4个网箱,则每个网箱的产量为16吨;如果放置7个网箱,则每个网箱的产量为10吨,由于该水域面积限制,最多只能放置10个网箱.
(1)试问放置多少个网箱时,总产量Q最高?
(2)若鱼的市场价为m万元/吨,养殖的总成本为(5lnx+1)万元.
(i)当m=0.25时,应放置多少个网箱才能使总收益y最大?
(ii)当m≥0.25时,求使得收益y最高的所有可能的x值组成的集合.【解析】(1)设p=ax+b,由已知得 所以
所以p=-2x+24,所以Q=px=(-2x+24)x=-2(x-6)2+72(x∈N*,
x≤10),所以当x=6时,f(x)最大,即放置6个网箱时,可使总
产量达到最大.
(2)总收益为y=f(x)=(-2x2+24x)m-(5ln x+1)(x∈N*,x≤10),
(i)当m=0.25时,f(x)=(-2x2+24x)× -(5ln x+1)=- x2+6x
-5ln x-1,所以f′(x)=当1<x<5时,f′(x)>0,当5<x<10时,f′(x)<0,所以
x=5时,函数取得极大值,也是最大值.所以应放置5个网箱才
能使总收益y最大;
(ii)当m≥0.25时,f(x)=(-2x2+24x)m-(5ln x+1),
所以f′(x)=
令f′(x)=0,即-4mx2+24mx-5=0,因为m≥0.25,所以
Δ=16m(36m-5)>0,方程-4mx2+24mx-5=0的两根分别为x1=3-
,x2=3+ ,因为m≥0.25,所以x1≤1,5≤x2<
6,所以当x∈(1,x2)时,f′(x)>0,当x2<x<10时,f′(x)<0,所以x=x2时,函数取得极大值,也是最大值.
所以使得收益y最高的所有可能的x值组成的集合为{5,6}.【补偿训练】某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y= +10(x-6)2,其中3
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.【解题指南】(1)根据“销售价格为5元/千克时,每日可售出该商品11千克”可知销售函数过点(5,11),将其代入可求得a的值.
(2)利润为f(x)=(每千克产品的售价-每千克产品的成本)×销售量,表示出函数解析式后,可借助导数求最值.【解析】(1)因为x=5时,y=11,所以 +10=11,所以a=2.
(2)由(1)可知,该商品每日的销售量y= +10(x-6)2,
所以商场每日销售该商品所获得的利润
f(x)=(x-3)[ +10(x-6)2]=2+10(x-3)(x-6)2,
3
于是,当x变化时,f′(x),f(x)的变化情况如下表,由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点.
所以,当x=4时,函数f(x)取得最大值,且最大值等于42.
答:当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.【规范解答】导数在解决实际问题中的应用
【典例】(12分)某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)2万件.
(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式.
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(a).【点题】警误区,促提升
失分点1:若在①处不能正确求出导数为0的点,即不舍x=12则会求错,本例最多得2分.
失分点2:若审题不清忽视对②处的讨论,仅求出一组,则本例最多得5分.
失分点3:若虽然进行了讨论,但无法确定函数取得最大值的点,即未能求出③处的值,则本例最多得7分.【悟题】提措施,导方向
1.应用分类讨论思想
在解含有参数的问题时,一定要注意分类讨论.如本例中销售价x由于管理费a的变化而变化,最终会影响利润的最大值.
2.注意限制条件的挖掘
对题目中的条件要认真分析,找出一些限制条件,如本例中x的取值,对于不符合条件的x的取值,要舍去.3.注意解题的规范性
解决实际应用题时,要注意解答过程的规范性,对于分类讨论得到的结果,如本例最大利润的结果表达式,要写成分段的形式,最后一定要进行总结.【类题试解】某工厂生产某种水杯,每个水杯的原材料费、加工费分别为30元、m元(m为常数,且2≤m≤3),设每个水杯的出厂价为x元(35≤x≤41),根据市场调查,水杯的日销售量与ex(e为自然对数的底数)成反比例,已知每个水杯的出厂价为40元时,日销售量为10个.
(1)求该工厂的日利润y(元)与每个水杯的出厂价x(元)的函数关系式.
(2)当每个水杯的出厂价为多少元时,该工厂的日利润最大,并求日利润的最大值.【解析】(1)设日销量为s,则s= ,因为x=40时,s=10,所以
10= ,所以k=10e40,所以s= .所以y= (x-30-
m)(35≤x≤41).
(2)y′= (31+m-x),令y′=0,可得x=31+m,所以当
2≤m≤3时,33≤31+m≤34,所以当35≤x≤41时,y′<0,函
数为减函数.所以当x=35时,y取最大值,最大值为10(5-
m)e5.
