1.5.1和1.5.2 曲边梯形的面积、汽车行驶的路程 课件1
文档属性
| 名称 | 1.5.1和1.5.2 曲边梯形的面积、汽车行驶的路程 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 00:00:00 | ||
图片预览









文档简介
课件48张PPT。1.5 定积分的概念
1.5.1 曲边梯形的面积
1.5.2 汽车行驶的路程 自主学习 新知突破1.理解连续函数的概念,了解定积分的实际背景及“以直代曲”“以不变代变”的思想方法.
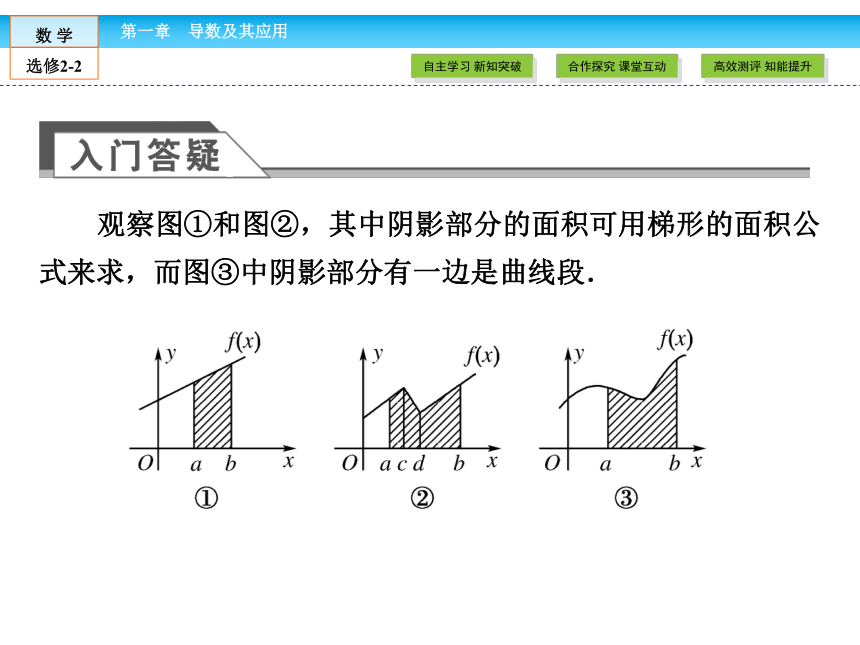
2.会用分割、近似代替、求和、取极限的方法求曲边梯形的面积和汽车行驶的路程.观察图①和图②,其中阴影部分的面积可用梯形的面积公式来求,而图③中阴影部分有一边是曲线段.
[问题] 如何求图③中阴影部分的面积呢?
[提示] 若把区间[a,b]分成许多小区间,进而把阴影部分拆分为一些小曲边梯形,近似地求出这些小曲边梯形的面积,分割的曲边梯形数目越多,所求得的面积越精确. 如果函数y=f(x)在某个区间I上的图象是一条__________的曲线,那么就把它称为区间I上的连续函数.连续函数连续不断1.曲边梯形:由直线x=a,x=b(a≠b),y=0和曲线y=f(x)所围成的图形称为曲边梯形(如图①).
2.求曲边梯形面积的方法与步骤:
(1)分割:把区间[a,b]分成许多小区间,进而把曲边梯形拆分为一些____________ (如图②);
(2)近似代替:对每个小曲边梯形“__________”,即用________的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的__________ (如图②);曲边梯形的面积 小曲边梯形以直代曲矩形近似值(3)求和:把以近似代替得到的每个小曲边梯形面积的近似值__________;
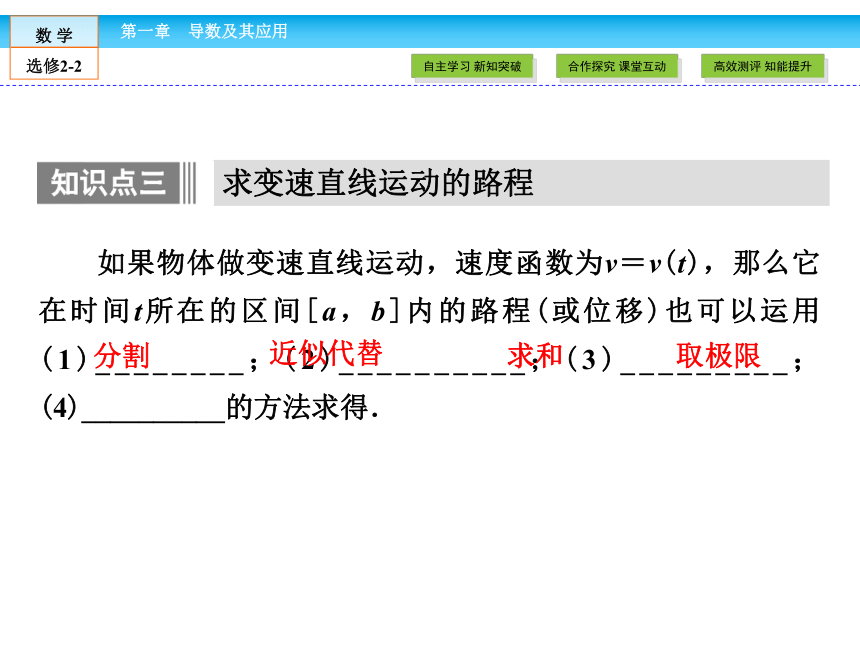
(4)取极限:当小曲边梯形的个数趋向无穷时,所有小曲边梯形的面积之和趋向一个_______,即为曲边梯形的面积.求和定值如果物体做变速直线运动,速度函数为v=v(t),那么它在时间t所在的区间[a,b]内的路程(或位移)也可以运用(1)________;(2)__________;(3)_________;(4)__________的方法求得.求变速直线运动的路程分割近似代替求和取极限2.汽车行驶的路程与曲边梯形的面积之间的关系
求汽车行驶的路程实际上也是求时间-速度坐标系中的曲边梯形的面积,所以求汽车行驶的路程与求曲边梯形的面积方法一样.1.在“近似代替”中,函数f(x)在区间[xi,xi+1]上的近似值( )
A.只能是左端点的函数值f(xi)
B.只能是右端点的函数值f(xi+1)
C.可以是该区间内任一点的函数值f(ξi)(ξi∈[xi,xi+1])
D.以上答案均正确
解析: 作近似计算时,Δx=xi+1-xi很小,误差可忽略,所以f(x)可以是[xi,xi+1]上任一值f(ξi).
答案: C
解析: 对于v=at+b,当a=0时为匀速直线运动,当a≠0时为匀变速直线运动,其中a>0时为匀加速直线运动,a<0时为匀减速直线运动,对于v=at2+bt+c(a≠0)及v=v(t)是t的三次、四次函数时,汽车做的都是变速(即变加速或变减速)直线运动,故B是错误的.
答案: B3.在计算由曲线y=-x2以及直线x=-1,x=1,y=0所围成的图形面积时,若将区间[-1,1]n等分,则每个小区间的长度为________.4.利用分割、近似代替、求和、取极限的办法求函数y=1+x,x=1,x=2的图象与x轴围成梯形的面积并用梯形的面积公式加以验证.合作探究 课堂互动 求曲边梯形的面积 求由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形面积. 求曲边梯形面积的四个步骤:
第一步:分割.在区间[a,b]中任意插入n-1个分点,将它等分成n个小区间[xi-1,xi](i=1,2…,n),区间[xi-1,xi]的长度Δxi=xi-xi-1,
第二步:近似代替,“以直代曲”.用矩形的面积近似代替小曲边梯形的面积,求出每个小曲边梯形面积的近似值.
第三步:求和.
第四步:取极限.
特别提醒:最后所得曲边梯形的面积不是近似值,而是真实值.1.求由抛物线y=x2与直线y=4所围成的平面图形的面积.求变速运动物体的路程 求自由落体的下落距离:
已知自由落体的运动速度v=gt,求在时间区间[0,t]内物体下落的距离.[思路点拨]
2.汽车行驶的速度为v=t2,求汽车在0≤t≤1这段时间内行驶的路程s.【错解】 (1)分割
将区间[0,1]等分为5个小区间:[0,0.2],[0.2,0.4],[0.4,0.6],[0.6,0.8],[0.8,1]
每个小区间的长度为0.2,过四个分点作x轴的垂线,把曲边梯形分成5个小曲边梯形,它们的面积分别记为ΔS1,ΔS2,…,ΔS5.【错因】 错解的原因是没有理解极限的思想.高效测评 知能提升 完成练习册作业谢谢观看!
1.5.1 曲边梯形的面积
1.5.2 汽车行驶的路程 自主学习 新知突破1.理解连续函数的概念,了解定积分的实际背景及“以直代曲”“以不变代变”的思想方法.
2.会用分割、近似代替、求和、取极限的方法求曲边梯形的面积和汽车行驶的路程.观察图①和图②,其中阴影部分的面积可用梯形的面积公式来求,而图③中阴影部分有一边是曲线段.
[问题] 如何求图③中阴影部分的面积呢?
[提示] 若把区间[a,b]分成许多小区间,进而把阴影部分拆分为一些小曲边梯形,近似地求出这些小曲边梯形的面积,分割的曲边梯形数目越多,所求得的面积越精确. 如果函数y=f(x)在某个区间I上的图象是一条__________的曲线,那么就把它称为区间I上的连续函数.连续函数连续不断1.曲边梯形:由直线x=a,x=b(a≠b),y=0和曲线y=f(x)所围成的图形称为曲边梯形(如图①).
2.求曲边梯形面积的方法与步骤:
(1)分割:把区间[a,b]分成许多小区间,进而把曲边梯形拆分为一些____________ (如图②);
(2)近似代替:对每个小曲边梯形“__________”,即用________的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的__________ (如图②);曲边梯形的面积 小曲边梯形以直代曲矩形近似值(3)求和:把以近似代替得到的每个小曲边梯形面积的近似值__________;
(4)取极限:当小曲边梯形的个数趋向无穷时,所有小曲边梯形的面积之和趋向一个_______,即为曲边梯形的面积.求和定值如果物体做变速直线运动,速度函数为v=v(t),那么它在时间t所在的区间[a,b]内的路程(或位移)也可以运用(1)________;(2)__________;(3)_________;(4)__________的方法求得.求变速直线运动的路程分割近似代替求和取极限2.汽车行驶的路程与曲边梯形的面积之间的关系
求汽车行驶的路程实际上也是求时间-速度坐标系中的曲边梯形的面积,所以求汽车行驶的路程与求曲边梯形的面积方法一样.1.在“近似代替”中,函数f(x)在区间[xi,xi+1]上的近似值( )
A.只能是左端点的函数值f(xi)
B.只能是右端点的函数值f(xi+1)
C.可以是该区间内任一点的函数值f(ξi)(ξi∈[xi,xi+1])
D.以上答案均正确
解析: 作近似计算时,Δx=xi+1-xi很小,误差可忽略,所以f(x)可以是[xi,xi+1]上任一值f(ξi).
答案: C
解析: 对于v=at+b,当a=0时为匀速直线运动,当a≠0时为匀变速直线运动,其中a>0时为匀加速直线运动,a<0时为匀减速直线运动,对于v=at2+bt+c(a≠0)及v=v(t)是t的三次、四次函数时,汽车做的都是变速(即变加速或变减速)直线运动,故B是错误的.
答案: B3.在计算由曲线y=-x2以及直线x=-1,x=1,y=0所围成的图形面积时,若将区间[-1,1]n等分,则每个小区间的长度为________.4.利用分割、近似代替、求和、取极限的办法求函数y=1+x,x=1,x=2的图象与x轴围成梯形的面积并用梯形的面积公式加以验证.合作探究 课堂互动 求曲边梯形的面积 求由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形面积. 求曲边梯形面积的四个步骤:
第一步:分割.在区间[a,b]中任意插入n-1个分点,将它等分成n个小区间[xi-1,xi](i=1,2…,n),区间[xi-1,xi]的长度Δxi=xi-xi-1,
第二步:近似代替,“以直代曲”.用矩形的面积近似代替小曲边梯形的面积,求出每个小曲边梯形面积的近似值.
第三步:求和.
第四步:取极限.
特别提醒:最后所得曲边梯形的面积不是近似值,而是真实值.1.求由抛物线y=x2与直线y=4所围成的平面图形的面积.求变速运动物体的路程 求自由落体的下落距离:
已知自由落体的运动速度v=gt,求在时间区间[0,t]内物体下落的距离.[思路点拨]
2.汽车行驶的速度为v=t2,求汽车在0≤t≤1这段时间内行驶的路程s.【错解】 (1)分割
将区间[0,1]等分为5个小区间:[0,0.2],[0.2,0.4],[0.4,0.6],[0.6,0.8],[0.8,1]
每个小区间的长度为0.2,过四个分点作x轴的垂线,把曲边梯形分成5个小曲边梯形,它们的面积分别记为ΔS1,ΔS2,…,ΔS5.【错因】 错解的原因是没有理解极限的思想.高效测评 知能提升 完成练习册作业谢谢观看!
