1.6 微积分基本定理 课件1
图片预览










文档简介
课件38张PPT。1.6 微积分基本定理 自主学习 新知突破1.直观了解并掌握微积分基本定理的含义.
2.会利用微积分基本定理求函数的定积分. 已知函数f(x)=2x+1,F(x)=x2+x,
[问题1] f(x)和F(x)有何关系?
[提示1] F′(x)=f(x).[问题3] 求F(2)-F(0)的值.
[提示3] F(2)-F(0)=4+2=6.
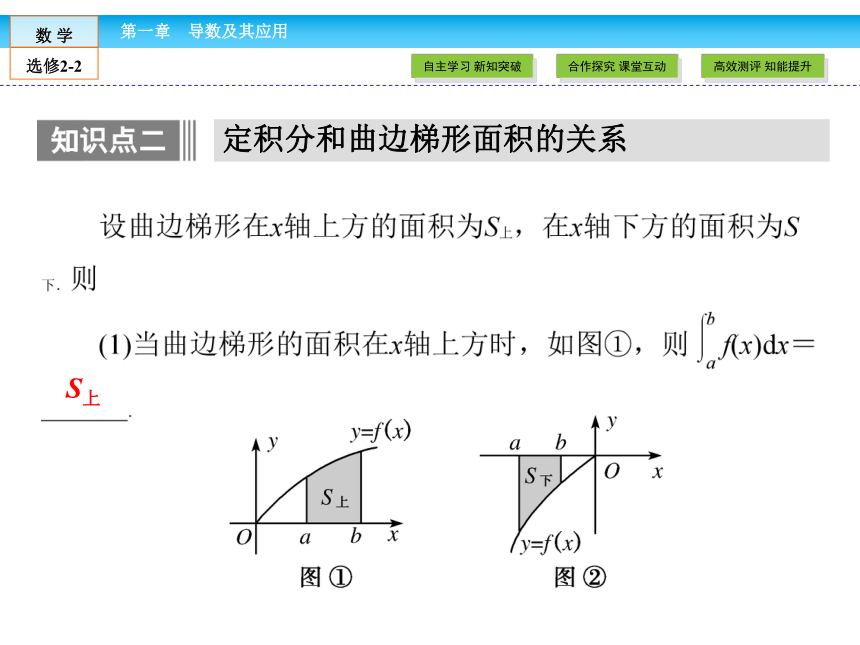
[问题4] 你得出什么结论?微积分基本定理 f(x) F(b)-F(a)连续 F(b)-F(a)定积分和曲边梯形面积的关系 S上 -S下 S上-S下0合作探究 课堂互动 求简单函数的定积分 求下列定积分:
[思路点拨] 先求被积函数的原函数,然后利用微积分基本定理求解. 求简单的定积分关键注意两点:
(1)掌握基本函数的导数以及导数的运算法则,正确求解被积函数的原函数,当原函数不易求时,可将被积函数适当变形后再求解;
(2)精确定位积分区间,分清积分下限与积分上限. 求复杂函数的定积分[思路点拨] 所求两个定积分的原函数都无法一眼看出,可以先把被积函数化简后,应用定积分的性质转化为易求原函数的定积分再求解. 求复杂函数定积分的方法:
(1)掌握基本初等函数的导数及导数的运算法则,正确求解被积函数的原函数.当原函数不易求解时,可以先把原函数变形.
(2)合理应用定积分的性质,把复杂函数的定积分转化为简单函数的定积分再求.
(3)准确确定积分区间,分清积分的上下限. 定积分的应用 [思路点拨] 定积分的应用体现了定积分与函数的内在联系,可以通过定积分构造新的函数,进而对这一函数进行性质、最值等方面的考查,解题过程中注意体会转化思想的应用. 高效测评 知能提升 完成练习册作业谢谢观看!
2.会利用微积分基本定理求函数的定积分. 已知函数f(x)=2x+1,F(x)=x2+x,
[问题1] f(x)和F(x)有何关系?
[提示1] F′(x)=f(x).[问题3] 求F(2)-F(0)的值.
[提示3] F(2)-F(0)=4+2=6.
[问题4] 你得出什么结论?微积分基本定理 f(x) F(b)-F(a)连续 F(b)-F(a)定积分和曲边梯形面积的关系 S上 -S下 S上-S下0合作探究 课堂互动 求简单函数的定积分 求下列定积分:
[思路点拨] 先求被积函数的原函数,然后利用微积分基本定理求解. 求简单的定积分关键注意两点:
(1)掌握基本函数的导数以及导数的运算法则,正确求解被积函数的原函数,当原函数不易求时,可将被积函数适当变形后再求解;
(2)精确定位积分区间,分清积分下限与积分上限. 求复杂函数的定积分[思路点拨] 所求两个定积分的原函数都无法一眼看出,可以先把被积函数化简后,应用定积分的性质转化为易求原函数的定积分再求解. 求复杂函数定积分的方法:
(1)掌握基本初等函数的导数及导数的运算法则,正确求解被积函数的原函数.当原函数不易求解时,可以先把原函数变形.
(2)合理应用定积分的性质,把复杂函数的定积分转化为简单函数的定积分再求.
(3)准确确定积分区间,分清积分的上下限. 定积分的应用 [思路点拨] 定积分的应用体现了定积分与函数的内在联系,可以通过定积分构造新的函数,进而对这一函数进行性质、最值等方面的考查,解题过程中注意体会转化思想的应用. 高效测评 知能提升 完成练习册作业谢谢观看!
