1.7.1 定积分在几何中的应用 课件1
文档属性
| 名称 | 1.7.1 定积分在几何中的应用 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 00:00:00 | ||
图片预览







文档简介
课件45张PPT。1.7 定积分的简单应用
1.7.1 定积分在几何中的应用自主学习 新知突破1.理解定积分的几何意义.
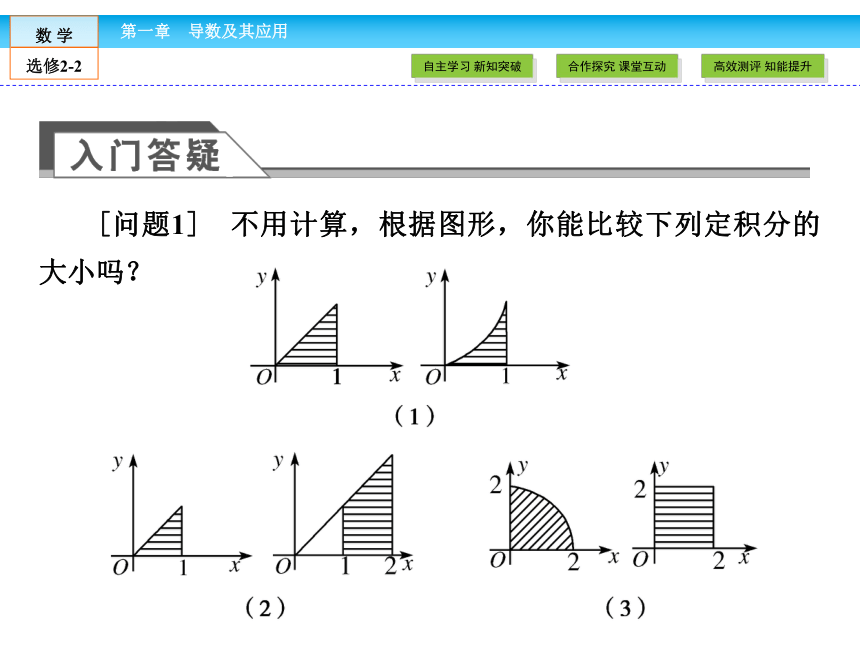
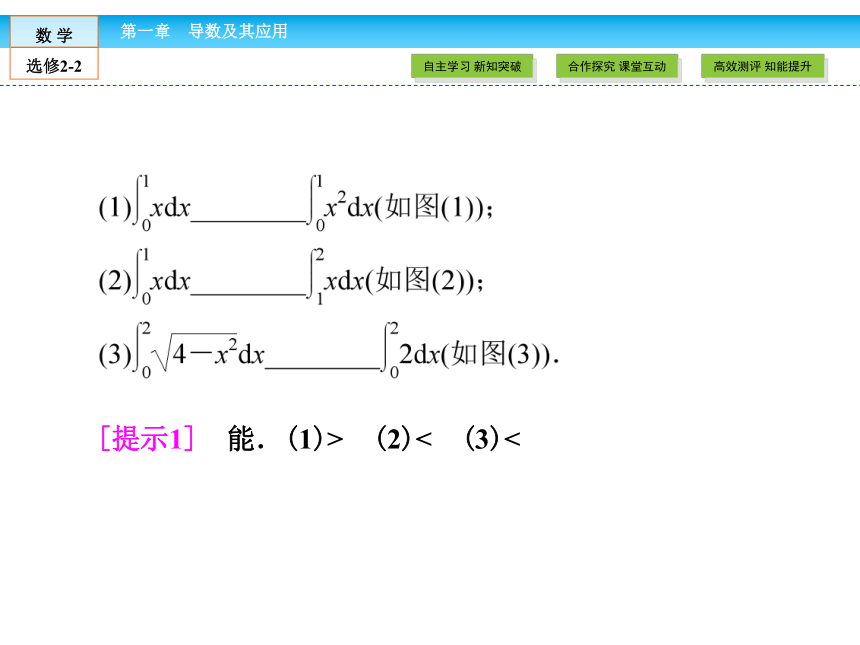
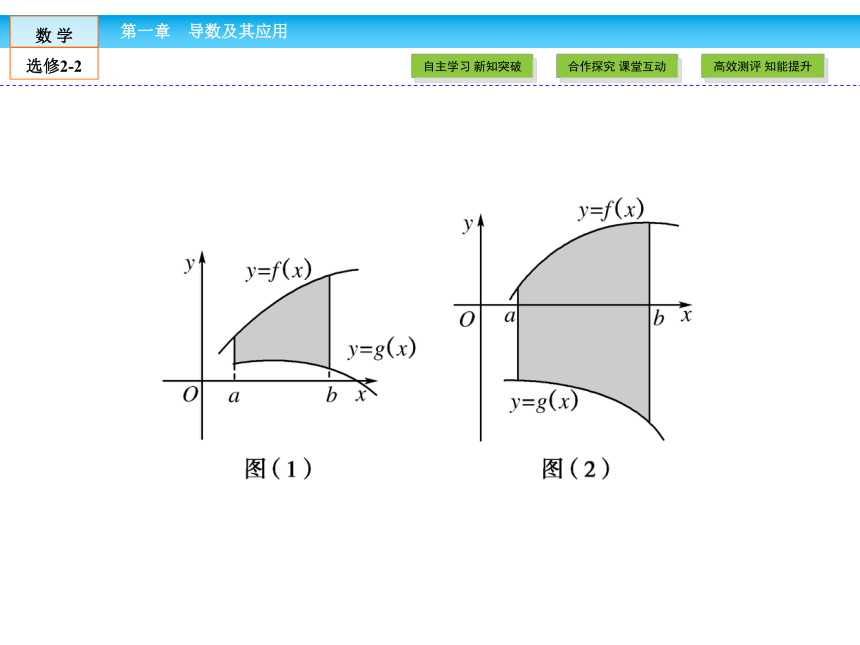
2.会通过定积分求由两条或多条曲线围成的平面图形的面积.[问题1] 不用计算,根据图形,你能比较下列定积分的大小吗?[提示1] 能.(1)> (2)< (3)<[提示2] 能.画出函数f(x)的图象如图.用定积分求平面图形的面积 1.画草图,求出曲线的__________.
2.将曲边形面积转化为____________面积.
3.根据图形特点选择适当的__________.
4.确定__________和__________.
5.计算定积分,求出面积.解由曲线所围的平面图形面积的解题步骤: 交点坐标曲边梯形的积分变量被积函数积分区间答案: C4.计算曲线y=x2-2x+3与直线y=x+3所围成图形的面积.合作探究 课堂互动 不分割图形面积的求解 1.用定积分求“曲边图形”面积的步骤:
(1)先画出草图,确定所求面积是哪部分;
(2)解方程组得到交点的坐标,确定被积函数以及积分的上、下限;
(3)把所求的面积用定积分表示;
(4)根据微积分基本定理求出面积.
2.注意事项:
(1)准确地画图,并合理分割图形;
(2)被积函数与积分上、下限要对应;
(3)当面积在x轴的下方时,面积是定积分的相反数.1.计算由曲线y2=x,y=x3围成的封闭图形的面积.
解析: 首先画出草图,如图.所求面积为图中阴影部分的面积.分割图形面积的求解 求抛物线y2=2x与直线y=4-x围成的平面图形的面积.
[思路点拨] 可先求出曲线与直线交点的横坐标,确定积分区间,然后分段利用公式求解. 由两条或两条以上的曲线围成的较为复杂的图形,在不同的区段内位于上方和下方的函数有所变化,通过解方程组求出曲线的不同的交点坐标,可以将积分区间进行细化分段,然后根据图象对各个区段分别求面积进而求和,在每个区段上被积函数均是由上减下;若积分变量选取x运算较为复杂,可以选y为积分变量,同时更改积分的上下限. 2.计算由曲线y=x2+2与直线y=3x,x=0,x=2所围图形的面积.定积分的综合应用 本题综合考查了导数的意义以及定积分等知识,运用待定系数法,先设出切点的坐标,利用导数的几何意义,建立了切线方程,然后利用定积分以及平面几何的性质求出所围成的平面图形的面积,根据条件建立方程求解,从而使问题得以解决. 3.如图所示,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.◎计算由曲线y=x2+2x(x≥-1)与直线x=-1,x=1及x轴所围图形的面积.【错因】 本题错解的原因是没有正确理解定积分的几何意义,因为曲线y=x2+2x(x≥-1)与直线x=-1及x轴所围图形在x轴的下方,面积取负号,因此错解所求的是面积的代数和,而非面积的和.高效测评 知能提升 完成练习册作业谢谢观看!
1.7.1 定积分在几何中的应用自主学习 新知突破1.理解定积分的几何意义.
2.会通过定积分求由两条或多条曲线围成的平面图形的面积.[问题1] 不用计算,根据图形,你能比较下列定积分的大小吗?[提示1] 能.(1)> (2)< (3)<[提示2] 能.画出函数f(x)的图象如图.用定积分求平面图形的面积 1.画草图,求出曲线的__________.
2.将曲边形面积转化为____________面积.
3.根据图形特点选择适当的__________.
4.确定__________和__________.
5.计算定积分,求出面积.解由曲线所围的平面图形面积的解题步骤: 交点坐标曲边梯形的积分变量被积函数积分区间答案: C4.计算曲线y=x2-2x+3与直线y=x+3所围成图形的面积.合作探究 课堂互动 不分割图形面积的求解 1.用定积分求“曲边图形”面积的步骤:
(1)先画出草图,确定所求面积是哪部分;
(2)解方程组得到交点的坐标,确定被积函数以及积分的上、下限;
(3)把所求的面积用定积分表示;
(4)根据微积分基本定理求出面积.
2.注意事项:
(1)准确地画图,并合理分割图形;
(2)被积函数与积分上、下限要对应;
(3)当面积在x轴的下方时,面积是定积分的相反数.1.计算由曲线y2=x,y=x3围成的封闭图形的面积.
解析: 首先画出草图,如图.所求面积为图中阴影部分的面积.分割图形面积的求解 求抛物线y2=2x与直线y=4-x围成的平面图形的面积.
[思路点拨] 可先求出曲线与直线交点的横坐标,确定积分区间,然后分段利用公式求解. 由两条或两条以上的曲线围成的较为复杂的图形,在不同的区段内位于上方和下方的函数有所变化,通过解方程组求出曲线的不同的交点坐标,可以将积分区间进行细化分段,然后根据图象对各个区段分别求面积进而求和,在每个区段上被积函数均是由上减下;若积分变量选取x运算较为复杂,可以选y为积分变量,同时更改积分的上下限. 2.计算由曲线y=x2+2与直线y=3x,x=0,x=2所围图形的面积.定积分的综合应用 本题综合考查了导数的意义以及定积分等知识,运用待定系数法,先设出切点的坐标,利用导数的几何意义,建立了切线方程,然后利用定积分以及平面几何的性质求出所围成的平面图形的面积,根据条件建立方程求解,从而使问题得以解决. 3.如图所示,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.◎计算由曲线y=x2+2x(x≥-1)与直线x=-1,x=1及x轴所围图形的面积.【错因】 本题错解的原因是没有正确理解定积分的几何意义,因为曲线y=x2+2x(x≥-1)与直线x=-1及x轴所围图形在x轴的下方,面积取负号,因此错解所求的是面积的代数和,而非面积的和.高效测评 知能提升 完成练习册作业谢谢观看!
