1.7.1 定积分在几何中的应用 课件4
文档属性
| 名称 | 1.7.1 定积分在几何中的应用 课件4 |  | |
| 格式 | zip | ||
| 文件大小 | 775.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 20:16:13 | ||
图片预览




文档简介
课件22张PPT。1.7 定积分的简单应用
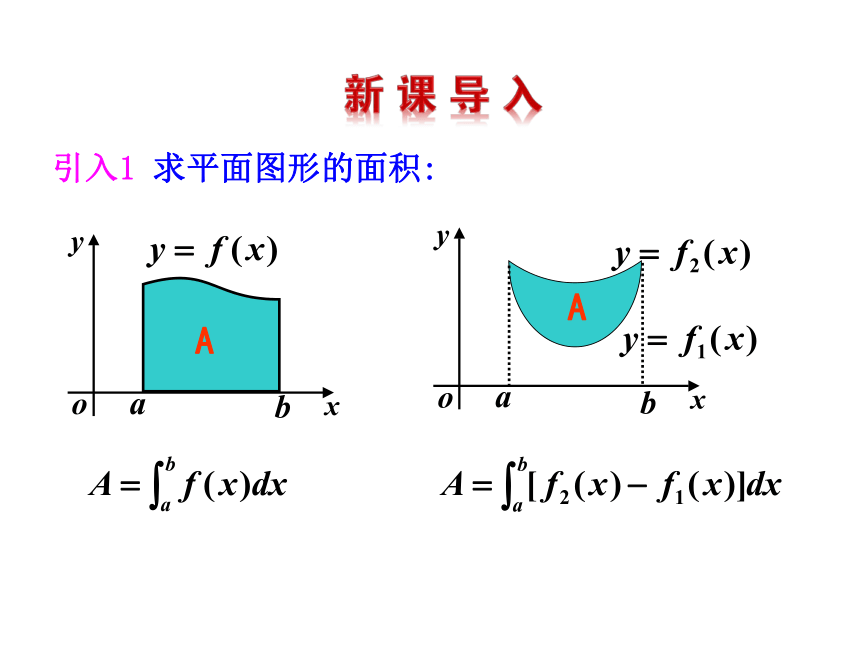
1.7.1 定积分在几何中的应用引入1 求平面图形的面积:引入2 求运动物体的位移 我们已经看到,定积分可以用来计算平面
图形的面积,求运动物体的位移,事实上,
定积分有着广泛的应用,下面我们就一起学习
定积分的简单应用吧!1.理解定积分的几何意义以及微积分的基本定理.
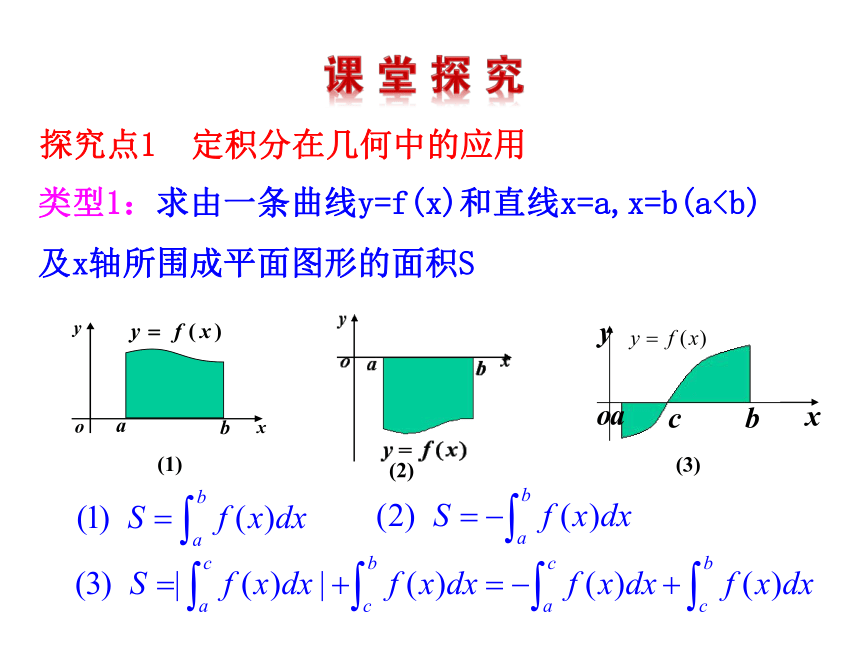
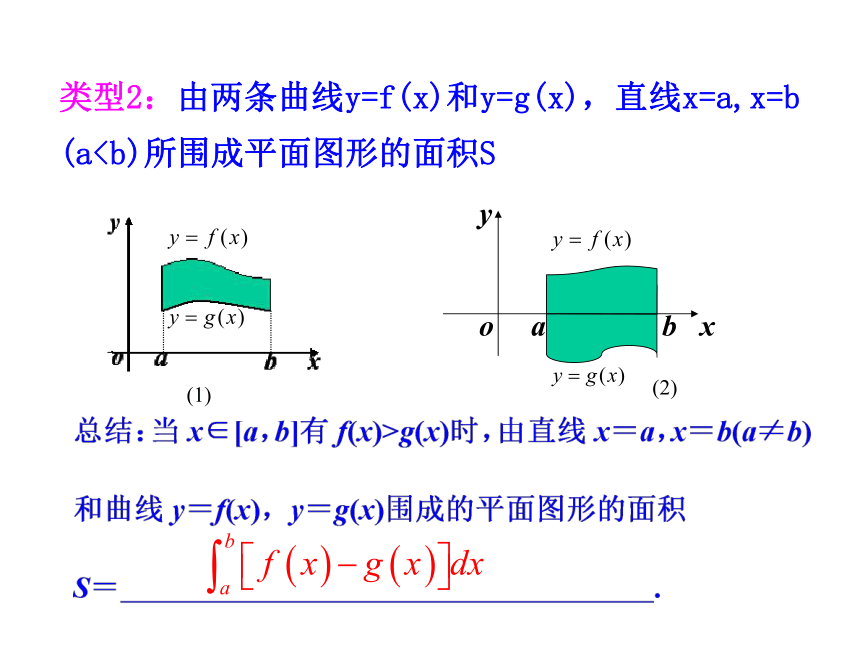
2.初步掌握利用定积分求曲边梯形的几种常见题型及方法. (重点、难点)类型1:求由一条曲线y=f(x)和直线x=a,x=b(a(a因此,所求图形的面积为【总结提升】
求两曲线围成的平面图形的面积的一般步骤:
(1)作出示意图;(弄清相对位置关系)
(2)求交点坐标,确定图形范围(积分的上限,下限)
(3)写出平面图形的定积分表达式;
(4)运用微积分基本定理计算定积分,求出面积.直线y=x-4与x轴交点为(4,0).
因此,所求图形的面积为解:作出直线y=x-4,曲线 的图象如图所示,所求面积为图中阴影部分面积.将所求平面图形的面积分割成左右两个部分.本题还有其他解法吗?另解1:将所求平面图形的面积分割成左右两个部分.还需要把函数y=x-4变形为x=y+4,函数 变形为另解2:将所求平面图形的面积看成位于y轴右边的一个梯形与一个曲边梯形的面积之差,因此取y为积分变量例3 求两抛物线y=8-x2,y=x2所围成的图形的面积.解析 作出曲线y=8-x2,y=x2的草图,所求面积为图中阴影部分的面积.
解方程组,
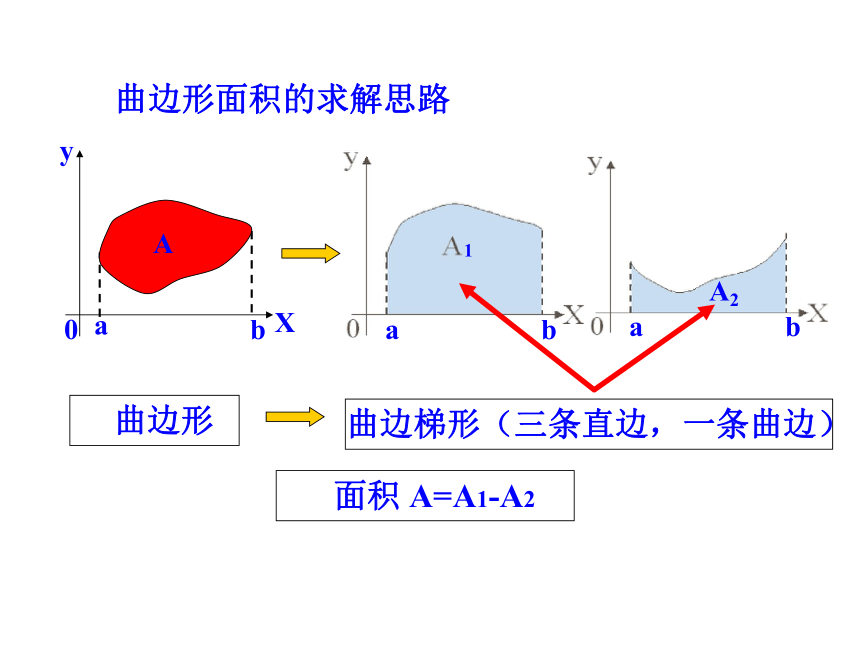
(1)求不分割图形面积的步骤为:画图形;
求交点(以确定积分上下限);用定积分表示再计算.
(2)一般原则上函数-下函数作被积函数.【总结提升】C4.求抛物线y=x2-1,直线x=2,y=0所围成的图形的面积.解:如图,由x2-1=0得到抛物线与x轴的交点坐标是(-1,0),(1,0).所求面积如图阴影所示:所以:5.如图,求曲线y=x2与直线y=2x所围图形的面积S.1.思想方法:数形结合及转化.
2.求两曲线围成的平面图形的面积的一般步骤:
(1)作出示意图;(弄清相对位置关系)
(2)求交点坐标,确定图形范围;(积分的上限,下限)
(3)写出平面图形的定积分表达式;
(4)运用微积分基本定理计算定积分,求出面积. 不闻不若闻之,闻之不若见之,见之不若知之,知之不若行之,学至于行而止矣.
——荀况
1.7.1 定积分在几何中的应用引入1 求平面图形的面积:引入2 求运动物体的位移 我们已经看到,定积分可以用来计算平面
图形的面积,求运动物体的位移,事实上,
定积分有着广泛的应用,下面我们就一起学习
定积分的简单应用吧!1.理解定积分的几何意义以及微积分的基本定理.
2.初步掌握利用定积分求曲边梯形的几种常见题型及方法. (重点、难点)类型1:求由一条曲线y=f(x)和直线x=a,x=b(a
求两曲线围成的平面图形的面积的一般步骤:
(1)作出示意图;(弄清相对位置关系)
(2)求交点坐标,确定图形范围(积分的上限,下限)
(3)写出平面图形的定积分表达式;
(4)运用微积分基本定理计算定积分,求出面积.直线y=x-4与x轴交点为(4,0).
因此,所求图形的面积为解:作出直线y=x-4,曲线 的图象如图所示,所求面积为图中阴影部分面积.将所求平面图形的面积分割成左右两个部分.本题还有其他解法吗?另解1:将所求平面图形的面积分割成左右两个部分.还需要把函数y=x-4变形为x=y+4,函数 变形为另解2:将所求平面图形的面积看成位于y轴右边的一个梯形与一个曲边梯形的面积之差,因此取y为积分变量例3 求两抛物线y=8-x2,y=x2所围成的图形的面积.解析 作出曲线y=8-x2,y=x2的草图,所求面积为图中阴影部分的面积.
解方程组,
(1)求不分割图形面积的步骤为:画图形;
求交点(以确定积分上下限);用定积分表示再计算.
(2)一般原则上函数-下函数作被积函数.【总结提升】C4.求抛物线y=x2-1,直线x=2,y=0所围成的图形的面积.解:如图,由x2-1=0得到抛物线与x轴的交点坐标是(-1,0),(1,0).所求面积如图阴影所示:所以:5.如图,求曲线y=x2与直线y=2x所围图形的面积S.1.思想方法:数形结合及转化.
2.求两曲线围成的平面图形的面积的一般步骤:
(1)作出示意图;(弄清相对位置关系)
(2)求交点坐标,确定图形范围;(积分的上限,下限)
(3)写出平面图形的定积分表达式;
(4)运用微积分基本定理计算定积分,求出面积. 不闻不若闻之,闻之不若见之,见之不若知之,知之不若行之,学至于行而止矣.
——荀况
