1.1.1 变化率问题 学案(无答案)
文档属性
| 名称 | 1.1.1 变化率问题 学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 147.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 20:40:46 | ||
图片预览


文档简介
1.1.1
变化率问题
学案
【学习目标】
1.了解变化率,理解平均变化率的概念;
2.
会求函数在某点处附近的平均变化率.
【重点难点】
平均变化率的概念
【学习过程】
一 问提的提出:
问题1
气球膨胀率
(
阅读课本第2页,填写并思考:)
从数学角度描述吹气球的过程这种现象:
气球的体积(单位:)与半径(单位:)之间的函数关系是_______________,
如果将半径表示为体积的函数,那么______________,
在吹气球问题中,当空气容量V从0增加到1L时,气球的
半径增加了___________,气球的平均膨胀率为_____________
类似的,当空气容量V从1L增加到2L时,气球的半径增加了___________,气球的平均膨胀率为__________________
可以看出,随着气球体积逐渐变大,它的平均膨胀率____,
思考:
当空气容量从V1增加到V2时,气球的平均膨胀率为__________________________,并且随着气球体积逐渐变大,它的平均膨胀率__________________.
问题2
高台跳水
(
阅读课本第3页,填写并思考:)
在高台跳水运动中,,运动员相对于水面的高度h(单位:
m)与起跳后的时间t(单位:s)存在函数关系_________________
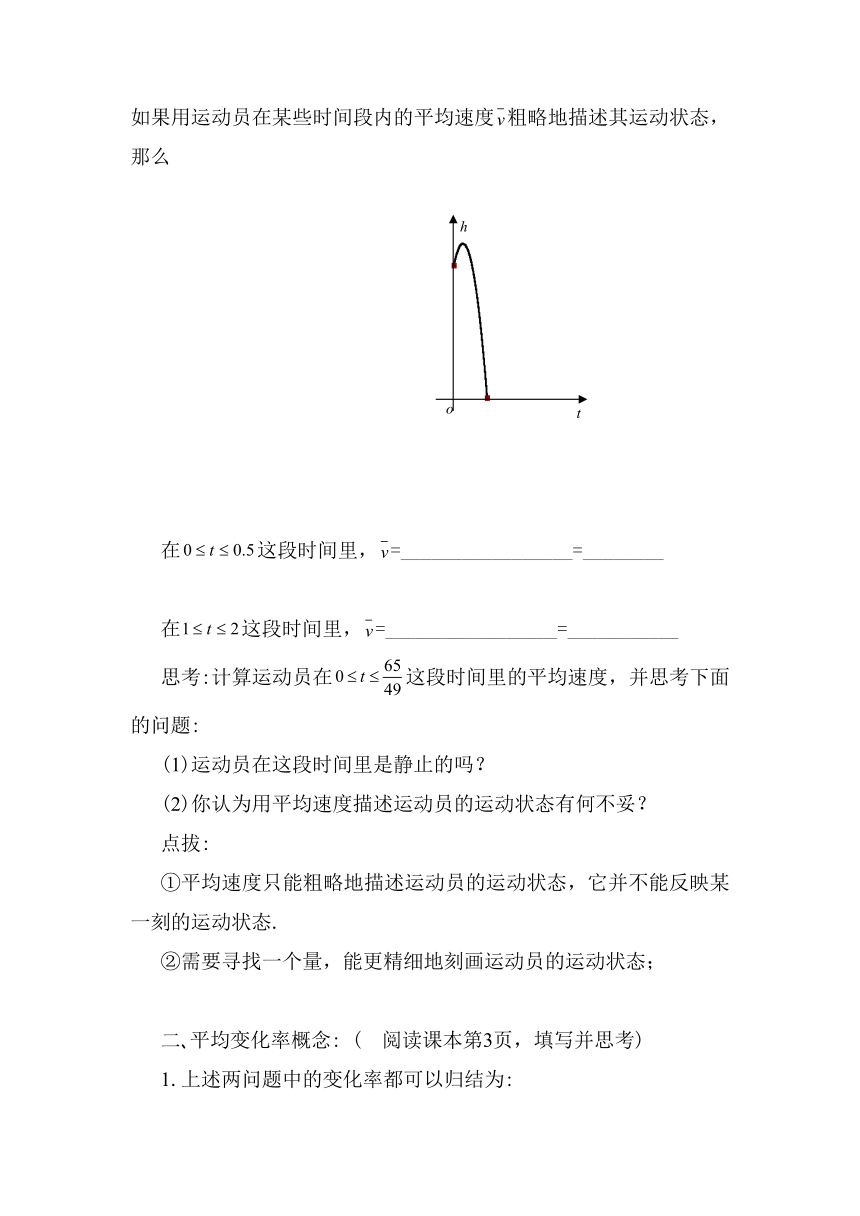
如果用运动员在某些时间段内的平均速度粗略地描述其运动状态,那么
在这段时间里,=_________________=________
在这段时间里,=_________________=___________
思考:计算运动员在这段时间里的平均速度,并思考下面的问题:
(1)运动员在这段时间里是静止的吗?
(2)你认为用平均速度描述运动员的运动状态有何不妥?
点拔:
①平均速度只能粗略地描述运动员的运动状态,它并不能反映某一刻的运动状态.
②需要寻找一个量,能更精细地刻画运动员的运动状态;
二 平均变化率概念:
(
阅读课本第3页,填写并思考)
1.上述两问题中的变化率都可以归结为:
对于函数y
=
f(x),问题中的变化率可用式子___________________________表示,
称为函数y
=
f(x)从x1到x2的平均变化率
2.习惯上设,
(这里看作是对于x1的一个“增量”可用x1+代替x2),
同样
)
3.
则平均变化率可表示为___________.
思考:
观察函数f(x)的图象
,平均变化率表示什么?
思考后分析,得结论:
(1)__________________________________
(2)计算函数y
=
f(x)平均变化率的步骤:
①求自变量的增量Δx=x2-x1;
②求函数值的增量Δy=f(x2)
-f(x1);
③求平均变化率
三.典例分析
例1.已知函数f(x)=的图象上的一点及临近一点,求此函数在A点处附近的变化率.
解:
例2.求在附近的平均变化率.
解:
四.课堂训练
1.质点运动规律为,则在时间中相应的平均速度为
.
2.物体按照S(t)=3t2+t+4的规律作直线运动,求在4s附近的平均变化率.
3.过曲线y=f(x)=x3上两点P(1,1)和Q
(1+Δx,1+Δy)作曲线的割线,求出当Δx=0.1时割线的斜率.
反思总结:1 平均变化率的概念
2 如何求函数在某点附近的平均变化率
课后作业
1 函数在区间上的平均变化率是(
)
A 4
B 2
C
D
2 经过函数图象上两点A B的直线的斜率()为_______;函数在区间[1,1.5]上的平均变化率为_________________
3 如果质点M按规律运动,则在时间[2,2.1]中相应的平均速度等于______
4 已知函数,分别计算在下列区间上的平均变化率
(1)[1,1.01]
(2)[0.9,1]
5 已知一次函数在区间[-2,6]上的平均变化率为2,且函数图象过点(0,2),试求此一次函数的表达式.
6 已知函数的图象上一点(1,1)及邻近一点(1+,)),求
7 将半径为R的球加热,若球的半径增加,则球的体积增量为:
8 求函数在附近的平均变化率,取都为,哪一点附近的平均变化率最大?
h
t
o
变化率问题
学案
【学习目标】
1.了解变化率,理解平均变化率的概念;
2.
会求函数在某点处附近的平均变化率.
【重点难点】
平均变化率的概念
【学习过程】
一 问提的提出:
问题1
气球膨胀率
(
阅读课本第2页,填写并思考:)
从数学角度描述吹气球的过程这种现象:
气球的体积(单位:)与半径(单位:)之间的函数关系是_______________,
如果将半径表示为体积的函数,那么______________,
在吹气球问题中,当空气容量V从0增加到1L时,气球的
半径增加了___________,气球的平均膨胀率为_____________
类似的,当空气容量V从1L增加到2L时,气球的半径增加了___________,气球的平均膨胀率为__________________
可以看出,随着气球体积逐渐变大,它的平均膨胀率____,
思考:
当空气容量从V1增加到V2时,气球的平均膨胀率为__________________________,并且随着气球体积逐渐变大,它的平均膨胀率__________________.
问题2
高台跳水
(
阅读课本第3页,填写并思考:)
在高台跳水运动中,,运动员相对于水面的高度h(单位:
m)与起跳后的时间t(单位:s)存在函数关系_________________
如果用运动员在某些时间段内的平均速度粗略地描述其运动状态,那么
在这段时间里,=_________________=________
在这段时间里,=_________________=___________
思考:计算运动员在这段时间里的平均速度,并思考下面的问题:
(1)运动员在这段时间里是静止的吗?
(2)你认为用平均速度描述运动员的运动状态有何不妥?
点拔:
①平均速度只能粗略地描述运动员的运动状态,它并不能反映某一刻的运动状态.
②需要寻找一个量,能更精细地刻画运动员的运动状态;
二 平均变化率概念:
(
阅读课本第3页,填写并思考)
1.上述两问题中的变化率都可以归结为:
对于函数y
=
f(x),问题中的变化率可用式子___________________________表示,
称为函数y
=
f(x)从x1到x2的平均变化率
2.习惯上设,
(这里看作是对于x1的一个“增量”可用x1+代替x2),
同样
)
3.
则平均变化率可表示为___________.
思考:
观察函数f(x)的图象
,平均变化率表示什么?
思考后分析,得结论:
(1)__________________________________
(2)计算函数y
=
f(x)平均变化率的步骤:
①求自变量的增量Δx=x2-x1;
②求函数值的增量Δy=f(x2)
-f(x1);
③求平均变化率
三.典例分析
例1.已知函数f(x)=的图象上的一点及临近一点,求此函数在A点处附近的变化率.
解:
例2.求在附近的平均变化率.
解:
四.课堂训练
1.质点运动规律为,则在时间中相应的平均速度为
.
2.物体按照S(t)=3t2+t+4的规律作直线运动,求在4s附近的平均变化率.
3.过曲线y=f(x)=x3上两点P(1,1)和Q
(1+Δx,1+Δy)作曲线的割线,求出当Δx=0.1时割线的斜率.
反思总结:1 平均变化率的概念
2 如何求函数在某点附近的平均变化率
课后作业
1 函数在区间上的平均变化率是(
)
A 4
B 2
C
D
2 经过函数图象上两点A B的直线的斜率()为_______;函数在区间[1,1.5]上的平均变化率为_________________
3 如果质点M按规律运动,则在时间[2,2.1]中相应的平均速度等于______
4 已知函数,分别计算在下列区间上的平均变化率
(1)[1,1.01]
(2)[0.9,1]
5 已知一次函数在区间[-2,6]上的平均变化率为2,且函数图象过点(0,2),试求此一次函数的表达式.
6 已知函数的图象上一点(1,1)及邻近一点(1+,)),求
7 将半径为R的球加热,若球的半径增加,则球的体积增量为:
8 求函数在附近的平均变化率,取都为,哪一点附近的平均变化率最大?
h
t
o
