1.1.3 导数的几何意义 同步练习2(含答案)
文档属性
| 名称 | 1.1.3 导数的几何意义 同步练习2(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 21:09:59 | ||
图片预览



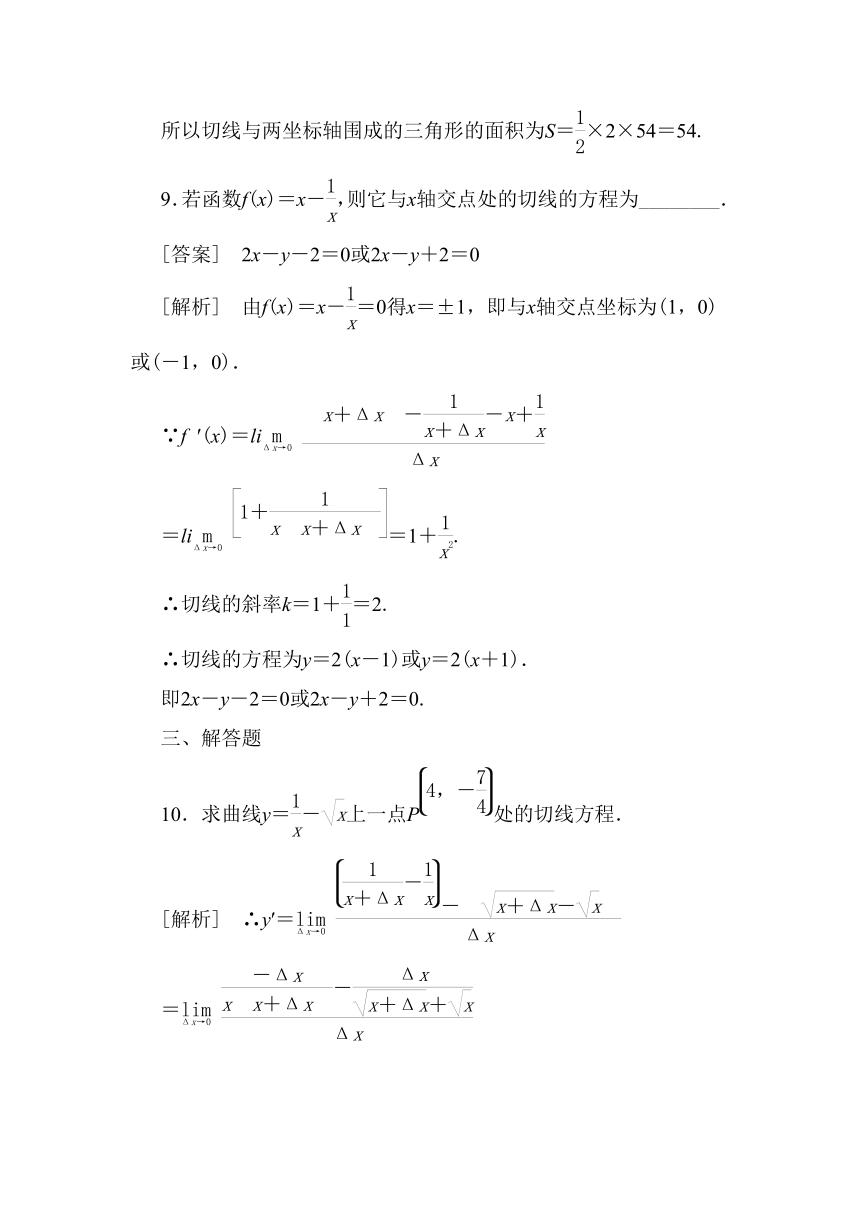
文档简介
1.1.3
导数的几何意义
同步练习
基础巩固强化
一、选择题
1.已知曲线y=2x3上一点A(1,2),则点A处的切线斜率等于( )
A.0
B.2
C.4
D.6
[答案] D
[解析] Δy=2(1+Δx)3-2×13=6(Δx)+6(Δx)2+(Δx)3,
=[(Δx)2+6Δx+6]=6,故选D.
2.设曲线y=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a等于( )
A.1
B.
C.-
D.-1
[答案] A
[解析] ∵y′|x=1=
=
=
(2a+aΔx)=2a,
∴2a=2,∴a=1.
3.曲线y=x3-2在点处切线的倾斜角为( )
A.1
B.
C.π
D.-
[答案] B
[解析] ∵y′=li
=li[x2+xΔx+(Δx)2]=x2,
∴切线的斜率k=y′|x=1=1.
∴切线的倾斜角为,故应选B.
4.设f
′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在
B.与x轴平行或重合
C.与x轴垂直
D.与x轴斜交
[答案] B
[解析] 由导数的几何意义知B正确,故应选B.
5.设f(x)为可导函数且满足
=-1,则过曲线y=f(x)上点(1,f(1))处的切线斜率为( )
A.2
B.-1
C.1
D.-2
[答案] B
[解析]
=
=
=f
′(1)=-1.
6.曲线y=x3+11在点P(1,12)处的切线与y轴交点的纵坐标是( )
A.-9
B.-3
C.9
D.15
[答案] C
[解析] 因为y′=
=
((Δx)2+3xΔx+3x2)=3x2,所以切线的斜率k=f
′(1)=3,又因为切点为P(1,12),故切线方程为3x-y+9=0,令x=0,得y=9.
二、填空题
7.已知函数f(x)=x3+2,则f
′(2)=________.
[答案] 12
[解析] f
′(2)=
=
=[4+4Δx+(Δx)2+4+2Δx+4]
=[12+6Δx+(Δx)2]=12.
8.曲线y=x3在点(3,27)处的切线与两坐标轴所围成的三角形的面积为________.
[答案] 54
[解析] 因为f
′(3)=li
=27,
所以在点(3,27)处的切线方程为y-27=27(x-3)即y=27x-54.
此切线与x轴、y轴的交点分别为(2,0),(0,-54).
所以切线与两坐标轴围成的三角形的面积为S=×2×54=54.
9.若函数f(x)=x-,则它与x轴交点处的切线的方程为________.
[答案] 2x-y-2=0或2x-y+2=0
[解析] 由f(x)=x-=0得x=±1,即与x轴交点坐标为(1,0)或(-1,0).
∵f
′(x)=li
=li
=1+.
∴切线的斜率k=1+=2.
∴切线的方程为y=2(x-1)或y=2(x+1).
即2x-y-2=0或2x-y+2=0.
三、解答题
10.求曲线y=-上一点P处的切线方程.
[解析] ∴y′=
=
=
=--
.
∴y′|x=4=--=-,
∴曲线在点P处的切线方程为:
y+=-(x-4).
即5x+16y+8=0.
能力拓展提升
一、选择题
11.已知直线ax-by-2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则为( )
A.
B.-
C.
D.-
[答案] D
[解析] 由导数的定义可得y′=3x2,
∴y=x3在点P(1,1)处的切线斜率k=y′|x=1=3,
由条件知,3×=-1,∴=-.
12.已知函数y=f(x)的图象在点(1,f(1))处的切线方程是x-2y+1=0,则f(1)+2f
′(1)的值是( )
A.
B.1
C.
D.2
[答案] D
[解析] ∵(1,f(1))在直线x-2y+1=0上,
∴1-2f(1)+1=0,∴f(1)=1.
又∵f
′(1)=,∴f(1)+2f
′(1)=1+2×=2.故选D.
13.已知y=f(x)的图象如图,则f
′(xA)与f
′(xB)的大小关系是( )
A.f
′(xA)>f
′(xB)
B.f
′(xA)′(xB)
C.f
′(xA)=f
′(xB)
D.不能确定
[答案] B
[解析] 由图可知,曲线在点A处的切线的斜率比曲线在点B处的切线的斜率小,结合导数的几何意义知f
′(xA)′(xB),选B.
二、填空题
14.如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则
=__________________.
[答案] -2
[解析] 由导数的概念和几何意义知,
=f
′(1)=kAB==-2.
15.设f(x)=f
′(1)+,则f(4)=________.
[答案]
[解析] f
′(1)=
=
=
=
=,
∴f(x)=+,
∴f(4)=+=.
三、解答题
16.已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程.
[解析] (1)y′=li
=3x2-3.
则过点P且以P(1,-2)为切点的直线的斜率
k1=f
′(1)=0,
∴所求直线方程为y=-2.
(2)设切点坐标为(x0,x-3x0),
则直线l的斜率k2=f
′(x0)=3x-3,
∴直线l的方程为y-(x-3x0)=(3x-3)(x-x0)
又直线l过点P(1,-2),
∴-2-
(x-3x0)=(3x-3)(1-x0),
∴x-3x0+2=(3x-3)(x0-1),∴(x0-1)2(2x0+1)=0,解得x0=1(舍去)或x0=-.
故所求直线斜率k=3x-3=-,
于是:y-(-2)=-(x-1),即9x+4y-1=0.
17.已知曲线y=x2+1,是否存在实数a,使得经过点(1,a)能够作出该曲线的两条切线?若存在,求出实数a的取值范围;若不存在,请说明理由.
[解析] ∵==2x+Δx,
∴y′=li
=li
(2x+Δx)=2x.
设切点为P(x0,y0),则切线的斜率为k=y′|x=x0=2x0,由点斜式可得所求切线方程为y-y0=2x0(x-x0).
又∵切线过点(1,a),且y0=x+1,
∴a-(x+1)=2x0(1-x0),
即x-2x0+a-1=0.∵切线有两条,
∴Δ=(-2)2-4(a-1)>0,解得a<2.
故存在实数a,使得经过点(1,a)能够作出该曲线的两条切线,a的取值范围是{a|a<2}.
导数的几何意义
同步练习
基础巩固强化
一、选择题
1.已知曲线y=2x3上一点A(1,2),则点A处的切线斜率等于( )
A.0
B.2
C.4
D.6
[答案] D
[解析] Δy=2(1+Δx)3-2×13=6(Δx)+6(Δx)2+(Δx)3,
=[(Δx)2+6Δx+6]=6,故选D.
2.设曲线y=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a等于( )
A.1
B.
C.-
D.-1
[答案] A
[解析] ∵y′|x=1=
=
=
(2a+aΔx)=2a,
∴2a=2,∴a=1.
3.曲线y=x3-2在点处切线的倾斜角为( )
A.1
B.
C.π
D.-
[答案] B
[解析] ∵y′=li
=li[x2+xΔx+(Δx)2]=x2,
∴切线的斜率k=y′|x=1=1.
∴切线的倾斜角为,故应选B.
4.设f
′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在
B.与x轴平行或重合
C.与x轴垂直
D.与x轴斜交
[答案] B
[解析] 由导数的几何意义知B正确,故应选B.
5.设f(x)为可导函数且满足
=-1,则过曲线y=f(x)上点(1,f(1))处的切线斜率为( )
A.2
B.-1
C.1
D.-2
[答案] B
[解析]
=
=
=f
′(1)=-1.
6.曲线y=x3+11在点P(1,12)处的切线与y轴交点的纵坐标是( )
A.-9
B.-3
C.9
D.15
[答案] C
[解析] 因为y′=
=
((Δx)2+3xΔx+3x2)=3x2,所以切线的斜率k=f
′(1)=3,又因为切点为P(1,12),故切线方程为3x-y+9=0,令x=0,得y=9.
二、填空题
7.已知函数f(x)=x3+2,则f
′(2)=________.
[答案] 12
[解析] f
′(2)=
=
=[4+4Δx+(Δx)2+4+2Δx+4]
=[12+6Δx+(Δx)2]=12.
8.曲线y=x3在点(3,27)处的切线与两坐标轴所围成的三角形的面积为________.
[答案] 54
[解析] 因为f
′(3)=li
=27,
所以在点(3,27)处的切线方程为y-27=27(x-3)即y=27x-54.
此切线与x轴、y轴的交点分别为(2,0),(0,-54).
所以切线与两坐标轴围成的三角形的面积为S=×2×54=54.
9.若函数f(x)=x-,则它与x轴交点处的切线的方程为________.
[答案] 2x-y-2=0或2x-y+2=0
[解析] 由f(x)=x-=0得x=±1,即与x轴交点坐标为(1,0)或(-1,0).
∵f
′(x)=li
=li
=1+.
∴切线的斜率k=1+=2.
∴切线的方程为y=2(x-1)或y=2(x+1).
即2x-y-2=0或2x-y+2=0.
三、解答题
10.求曲线y=-上一点P处的切线方程.
[解析] ∴y′=
=
=
=--
.
∴y′|x=4=--=-,
∴曲线在点P处的切线方程为:
y+=-(x-4).
即5x+16y+8=0.
能力拓展提升
一、选择题
11.已知直线ax-by-2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则为( )
A.
B.-
C.
D.-
[答案] D
[解析] 由导数的定义可得y′=3x2,
∴y=x3在点P(1,1)处的切线斜率k=y′|x=1=3,
由条件知,3×=-1,∴=-.
12.已知函数y=f(x)的图象在点(1,f(1))处的切线方程是x-2y+1=0,则f(1)+2f
′(1)的值是( )
A.
B.1
C.
D.2
[答案] D
[解析] ∵(1,f(1))在直线x-2y+1=0上,
∴1-2f(1)+1=0,∴f(1)=1.
又∵f
′(1)=,∴f(1)+2f
′(1)=1+2×=2.故选D.
13.已知y=f(x)的图象如图,则f
′(xA)与f
′(xB)的大小关系是( )
A.f
′(xA)>f
′(xB)
B.f
′(xA)
C.f
′(xA)=f
′(xB)
D.不能确定
[答案] B
[解析] 由图可知,曲线在点A处的切线的斜率比曲线在点B处的切线的斜率小,结合导数的几何意义知f
′(xA)
二、填空题
14.如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则
=__________________.
[答案] -2
[解析] 由导数的概念和几何意义知,
=f
′(1)=kAB==-2.
15.设f(x)=f
′(1)+,则f(4)=________.
[答案]
[解析] f
′(1)=
=
=
=
=,
∴f(x)=+,
∴f(4)=+=.
三、解答题
16.已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程.
[解析] (1)y′=li
=3x2-3.
则过点P且以P(1,-2)为切点的直线的斜率
k1=f
′(1)=0,
∴所求直线方程为y=-2.
(2)设切点坐标为(x0,x-3x0),
则直线l的斜率k2=f
′(x0)=3x-3,
∴直线l的方程为y-(x-3x0)=(3x-3)(x-x0)
又直线l过点P(1,-2),
∴-2-
(x-3x0)=(3x-3)(1-x0),
∴x-3x0+2=(3x-3)(x0-1),∴(x0-1)2(2x0+1)=0,解得x0=1(舍去)或x0=-.
故所求直线斜率k=3x-3=-,
于是:y-(-2)=-(x-1),即9x+4y-1=0.
17.已知曲线y=x2+1,是否存在实数a,使得经过点(1,a)能够作出该曲线的两条切线?若存在,求出实数a的取值范围;若不存在,请说明理由.
[解析] ∵==2x+Δx,
∴y′=li
=li
(2x+Δx)=2x.
设切点为P(x0,y0),则切线的斜率为k=y′|x=x0=2x0,由点斜式可得所求切线方程为y-y0=2x0(x-x0).
又∵切线过点(1,a),且y0=x+1,
∴a-(x+1)=2x0(1-x0),
即x-2x0+a-1=0.∵切线有两条,
∴Δ=(-2)2-4(a-1)>0,解得a<2.
故存在实数a,使得经过点(1,a)能够作出该曲线的两条切线,a的取值范围是{a|a<2}.
