1.1.3 导数的几何意义 同步练习3(含答案)
文档属性
| 名称 | 1.1.3 导数的几何意义 同步练习3(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 131.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 21:10:27 | ||
图片预览


文档简介
1.1.3
导数的几何意义
同步练习
一、选择题
1.设f′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在
B.与x轴平行或重合
C.与x轴垂直
D.与x轴斜交
答案 B
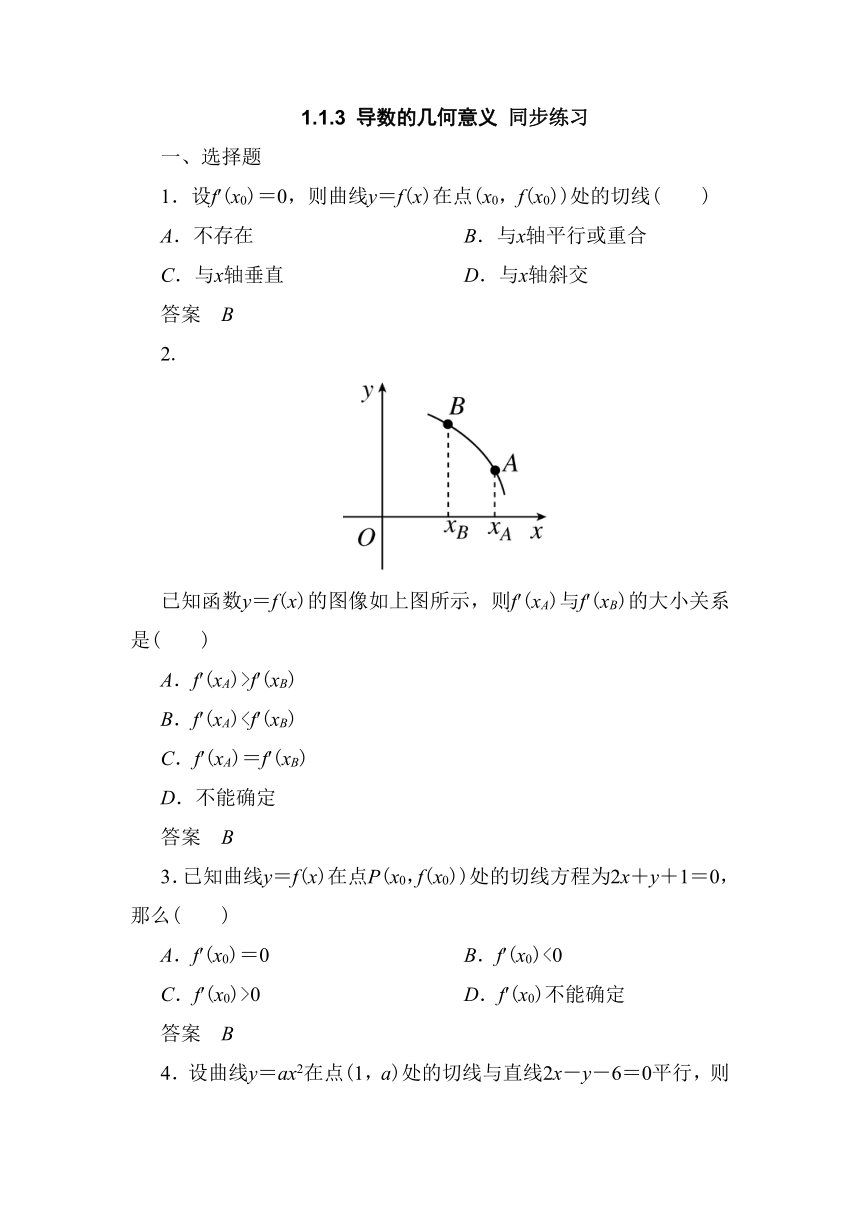
2.
已知函数y=f(x)的图像如上图所示,则f′(xA)与f′(xB)的大小关系是( )
A.f′(xA)>f′(xB)
B.f′(xA)C.f′(xA)=f′(xB)
D.不能确定
答案 B
3.已知曲线y=f(x)在点P(x0,f(x0))处的切线方程为2x+y+1=0,那么( )
A.f′(x0)=0
B.f′(x0)<0
C.f′(x0)>0
D.f′(x0)不能确定
答案 B
4.设曲线y=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a等于( )
A.1
B.
C.-
D.-1
答案 A
5.如果曲线y=f(x)在点(x0,f(x0))处的切线方程为x+2y-3=0,那么( )
A.f′(x0)>0
B.f′(x0)<0
C.f′(x0)=0
D.f′(x0)不存在
答案 B
6.下列说法正确的是( )
A.曲线的切线和曲线有交点,这点一定是切点
B.过曲线上一点作曲线的切线,这点一定是切点
C.若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处无切线
D.若曲线y=f(x)在点(x0,f(x0))处有切线,则f′(x0)不一定存在
答案 D
7.在曲线y=x2上切线的倾斜角为的点是( )
A.(0,0)
B.(2,4)
C.(,)
D.(,)
答案 D
8.设f(x)=,则
等于( )
A.-
B.
C.-
D.
答案 D
解析
=
=.
9.若f(x)=x3+x-1,f′(x0)=4,则x0的值为( )
A.1
B.-1
C.±1
D.±3
答案 C
解析 f′(x0)=
=
=
[3x0+1+3x0·Δx+(Δx)2]
=3x0+1=4.解得x0=±1.
10.已知曲线y=2x3上一点A(1,2),则A处的切线斜率等于( )
A.2
B.4
C.6+6·Δx+2·(Δx)2
D.6
答案 D
二、填空题
11.已知函数y=f
(x)的图像在点M(1,f(1))处的切线方程是y=x+2,则f(1)+f′(1)=________.
答案 3
解析 f′(1)=,f
(1)=×1+2=,∴f(1)+f′(1)=3.
三、解答题
12.求曲线y=2x-x3在点(-1,-1)处的切线的方程及此切线与x轴、y轴所围成的平面图形的面积.
答案 x+y+2=0;2
13.若曲线y=2x3上某点切线的斜率等于6,求此点的坐标.
解析 ∵y′|x=x0=
=6x0,
∴6x0=6.∴x0=±1.故(1,2),(-1,-2)为所求.
14.已知曲线C:y=x3,求在曲线C上横坐标为1的点处的切线方程.
解析 将x=1代入曲线C的方程得y=1,
∴切点P(1,1).
∵y′=
=
=
=[3x2+3xΔx+(Δx)2]=3x2,
∴y′|x=1=3.
∴过P点的切线方程为y-1=3(x-1),
即3x-y-2=0.
重点班·选做题
15.点P在曲线y=f(x)=x2+1上,且曲线在点P处的切线与曲线y=-2x2-1相切,求点P的坐标.
解析 设P(x0,y0),则y0=x+1.
f′(x0)=
=2x0.
所以过点P的切线方程为y-y0=2x0(x-x0),
即y=2x0x+1-x.
而此直线与曲线y=-2x2-1相切,
所以切线与曲线y=-2x2-1只有一个公共点.
由得
2x2+2x0x+2-x=0.
即Δ=4x-8(2-x)=0.
解得x0=,y0=.
所以点P的坐标为(,)或(-,).
导数的几何意义
同步练习
一、选择题
1.设f′(x0)=0,则曲线y=f(x)在点(x0,f(x0))处的切线( )
A.不存在
B.与x轴平行或重合
C.与x轴垂直
D.与x轴斜交
答案 B
2.
已知函数y=f(x)的图像如上图所示,则f′(xA)与f′(xB)的大小关系是( )
A.f′(xA)>f′(xB)
B.f′(xA)
D.不能确定
答案 B
3.已知曲线y=f(x)在点P(x0,f(x0))处的切线方程为2x+y+1=0,那么( )
A.f′(x0)=0
B.f′(x0)<0
C.f′(x0)>0
D.f′(x0)不能确定
答案 B
4.设曲线y=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a等于( )
A.1
B.
C.-
D.-1
答案 A
5.如果曲线y=f(x)在点(x0,f(x0))处的切线方程为x+2y-3=0,那么( )
A.f′(x0)>0
B.f′(x0)<0
C.f′(x0)=0
D.f′(x0)不存在
答案 B
6.下列说法正确的是( )
A.曲线的切线和曲线有交点,这点一定是切点
B.过曲线上一点作曲线的切线,这点一定是切点
C.若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处无切线
D.若曲线y=f(x)在点(x0,f(x0))处有切线,则f′(x0)不一定存在
答案 D
7.在曲线y=x2上切线的倾斜角为的点是( )
A.(0,0)
B.(2,4)
C.(,)
D.(,)
答案 D
8.设f(x)=,则
等于( )
A.-
B.
C.-
D.
答案 D
解析
=
=.
9.若f(x)=x3+x-1,f′(x0)=4,则x0的值为( )
A.1
B.-1
C.±1
D.±3
答案 C
解析 f′(x0)=
=
=
[3x0+1+3x0·Δx+(Δx)2]
=3x0+1=4.解得x0=±1.
10.已知曲线y=2x3上一点A(1,2),则A处的切线斜率等于( )
A.2
B.4
C.6+6·Δx+2·(Δx)2
D.6
答案 D
二、填空题
11.已知函数y=f
(x)的图像在点M(1,f(1))处的切线方程是y=x+2,则f(1)+f′(1)=________.
答案 3
解析 f′(1)=,f
(1)=×1+2=,∴f(1)+f′(1)=3.
三、解答题
12.求曲线y=2x-x3在点(-1,-1)处的切线的方程及此切线与x轴、y轴所围成的平面图形的面积.
答案 x+y+2=0;2
13.若曲线y=2x3上某点切线的斜率等于6,求此点的坐标.
解析 ∵y′|x=x0=
=6x0,
∴6x0=6.∴x0=±1.故(1,2),(-1,-2)为所求.
14.已知曲线C:y=x3,求在曲线C上横坐标为1的点处的切线方程.
解析 将x=1代入曲线C的方程得y=1,
∴切点P(1,1).
∵y′=
=
=
=[3x2+3xΔx+(Δx)2]=3x2,
∴y′|x=1=3.
∴过P点的切线方程为y-1=3(x-1),
即3x-y-2=0.
重点班·选做题
15.点P在曲线y=f(x)=x2+1上,且曲线在点P处的切线与曲线y=-2x2-1相切,求点P的坐标.
解析 设P(x0,y0),则y0=x+1.
f′(x0)=
=2x0.
所以过点P的切线方程为y-y0=2x0(x-x0),
即y=2x0x+1-x.
而此直线与曲线y=-2x2-1相切,
所以切线与曲线y=-2x2-1只有一个公共点.
由得
2x2+2x0x+2-x=0.
即Δ=4x-8(2-x)=0.
解得x0=,y0=.
所以点P的坐标为(,)或(-,).
