1.3.1 函数的单调性与导数 同步练习3(含答案)
文档属性
| 名称 | 1.3.1 函数的单调性与导数 同步练习3(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 142.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 00:00:00 | ||
图片预览



文档简介
1.3.1
函数的单调性与导数
同步练习
一、选择题
1.函数f(x)=2x-sin
x在(-∞,+∞)上( )
A.是增函数
B.是减函数
C.有最大值
D.有最小值
答案 A
2.函数f(x)=5x2-2x的单调递减区间是( )
A.(,+∞)
B.(-∞,)
C.(-,+∞)
D.(-∞,-)
答案 B
3.函数y=xlnx在区间(0,1)上是( )
A.单调增函数
B.单调减函数
C.在(0,)上是减函数,在(,1)上是增函数
D.在(0,)上是增函数,在(,1)上是减函数
答案 C
解析 f′(x)=lnx+1,当0当0.
4.函数y=4x2+的单调增区间为( )
A.(0,+∞)
B.(,+∞)
C.(-∞,-1)
D.(-∞,-)
答案 B
解析 y′=8x-,令y′>0,得8x->0,
即x3>,
∴x>.
5.若函数y=a(x3-x)的递减区间为(-,),则a的取值范围是( )
A.a>0
B.-1<a<0
C.a>1
D.0<a<1
答案 A
解析 y′=a(3x2-1),解3x2-1<0,得-<x<.
∴f(x)=x3-x在(-,)上为减函数.
又y=a·(x3-x)的递减区间为(-,).
∴a>0.
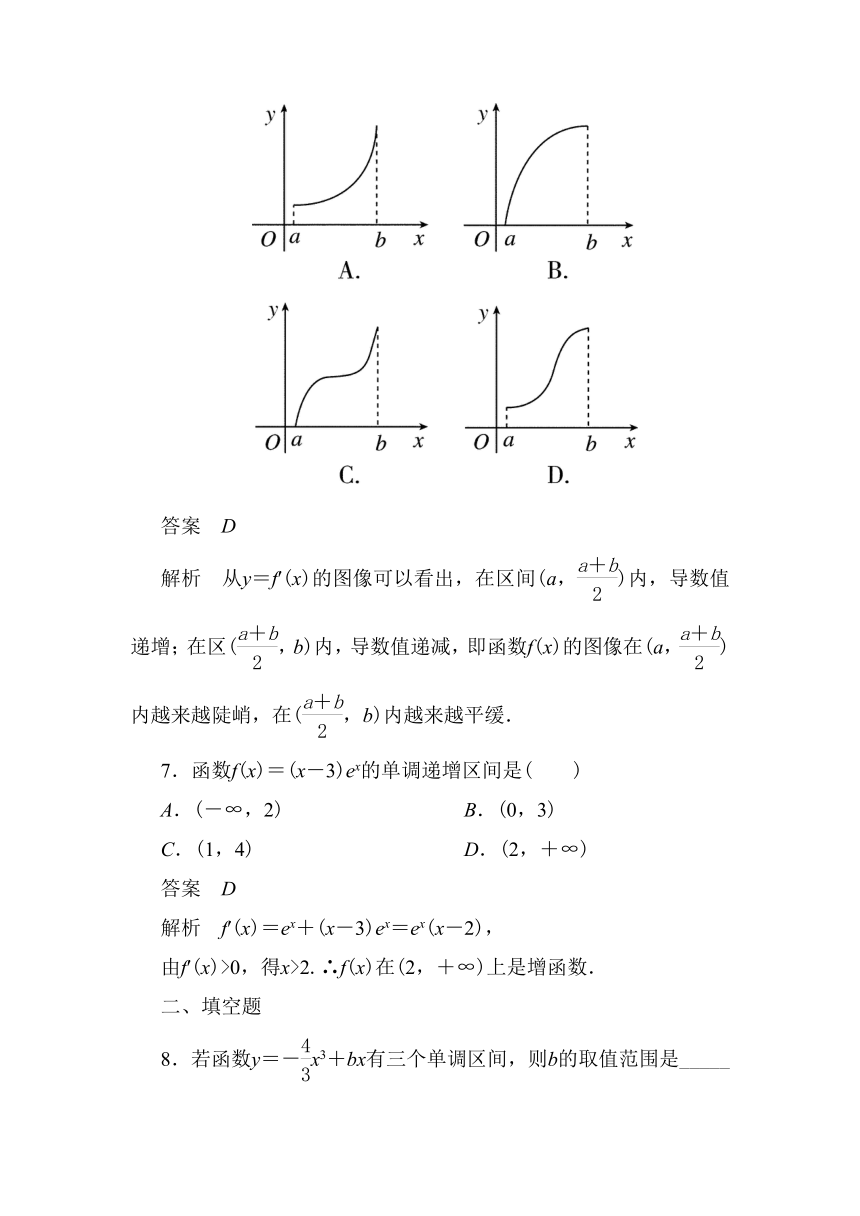
6.
已知f′(x)是f(x)的导函数,y=f′(x)的图像如图所示,则f(x)的图像只可能是( )
答案 D
解析 从y=f′(x)的图像可以看出,在区间(a,)内,导数值递增;在区(,b)内,导数值递减,即函数f(x)的图像在(a,)内越来越陡峭,在(,b)内越来越平缓.
7.函数f(x)=(x-3)ex的单调递增区间是( )
A.(-∞,2)
B.(0,3)
C.(1,4)
D.(2,+∞)
答案 D
解析 f′(x)=ex+(x-3)ex=ex(x-2),
由f′(x)>0,得x>2.∴f(x)在(2,+∞)上是增函数.
二、填空题
8.若函数y=-x3+bx有三个单调区间,则b的取值范围是________.
答案 (0,+∞)
解析 若函数y=-x3+bx有三个单调区间,则其导数y′=-4x2+b=0有两个不相等的实数根,所以b>0.
9.若函数f(x)=x-+在(1,+∞)上是增函数,则实数p的取值范围是________.
答案 [-1,+∞)
解析 f′(x)=1+≥0对x>1恒成立,即x2+p≥0对x>1恒成立,∴p≥-x2(x>1).∴p≥-1.
10.若函数y=ax3-ax2-2ax(a≠0)在[-1,2]上为增函数,则a∈________.
答案 (-∞,0)
解析 y′=ax2-ax-2a=a(x+1)(x-2)>0,
∵当x∈(-1,2)时,(x+1)(x-2)<0,
∴a<0.
11.f(x)=(x∈R)在区间[-1,1]上是增函数,则a∈________.
答案 [-1,1]
解析 y′=2·,
∵f(x)在[-1,1]上是增函数,∴y′在(-1,1)上大于等于0,即2·≥0.
∵(x2+2)2>0,
∴x2-ax-2≤0对x∈(-1,1)恒成立.
令g(x)=x2-ax-2,
则 即 ∴-1≤a≤1.
即a的取值范围是[-1,1].
三、解答题
12.已知f(x)=ax3+3x2-x-1在R上是减函数,求a的取值范围.
解析 ∵f′(x)=3ax2+6x-1,又f(x)在R上递减,
∴f′(x)≤0对x∈R恒成立.
即3ax2+6x-1≤0对x∈R恒成立,显然a≠0.
∴ ∴a≤-3.
即a的取值范围为(-∞,-3].
13.已知函数f(x)=x2+(x≠0,常数a∈R).若函数
f(x)在[2,+∞)上是单调递增的,求a的取值范围.
解析 f′(x)=2x-=,
要使f(x)在[2,+∞)上是单调递增的,
则f′(x)≥0在x∈[2,+∞)时恒成立,
即≥0在x∈[2,+∞)时恒成立.
∵x>0,∴2x3-a≥0,∴a≤2x3在x∈[2,+∞)上恒成立.
∴a≤(2x3)min.
∵x∈[2,+∞),y=2x3是单调递增的,
∴(2x3)min=16,∴a≤16.
当a=16时,
f′(x)=≥0(x∈[2,+∞))有且只有f′(2)=0.
∴a的取值范围是a≤16.
14.已知函数f(x)=x3+ax2+1,a∈R.
(1)讨论函数f(x)的单调区间;
(2)设函数f(x)在区间(-,-)内是减函数,求a的取值范围.
解析 (1)对f(x)求导,得
f′(x)=3x2+2ax=3x(x+a).
①当a=0时,f′(x)=3x2≥0恒成立.
∴f(x)的递增区间是(-∞,+∞);
②当a>0时,由于f′(x)分别在(-∞,-α)和(0,+∞)上都恒为正,所以f(x)的递增区间是(-∞,-a),(0,+∞);由于f′(x)在(-a,0)上恒为负,所以f(x)的递减区间是(-a,0);
③当a<0时,在x∈(-∞,0)和x∈(-a,+∞)上均有f′(x)>0,∴f(x)的递增区间是(-∞,0),(-a,+∞);在(0,-a)上,f′(x)<0,f(x)的递减区间是(0,-a).
(2)由(1)知,(-,-) (-a,0),
∴-a≤-.∴a≥1.
15.若函数f(x)=x3-ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围.
分析 本题主要考查借助函数的单调性来求导的能力及解不等式的能力.
解析 ∵f′(x)=x2-ax+a-1,令f′(x)=0,
解得x=1或x=a-1.
当a-1≤1,即a≤2时,函数f(x)在(1,+∞)上为增函数,不符合题意.
当a-1>1,即a>2时,函数f(x)在(-∞,1)上为增函数,在(1,a-1)上为减函数,在(a-1,+∞)上为增函数.
而当x∈(1,4)时,f′(x)<0;
当x∈(6,+∞)时,f′(x)>0.
∴4≤a-1≤6,即5≤a≤7.
∴a的取值范围是[5,7].
16.已知f(x)=在区间[1,+∞)上是增函数,求实数a的取值范围.
解析 因为f(x)=x-+,所以f′(x)=1+.
又f(x)在[1,+∞)上是增函数,
所以当x∈[1,+∞)时,恒有f′(x)=1+≥0,
即a≥-x2,x∈[1,+∞).所以a≥-1.
故所求a的取值范围是[-1,+∞).
17.已知函数f(x)=x3+ax2+bx,且f′(-1)=0.
(1)试用含a
代数式表示b;
(2)求f(x)的单调区间.
分析 可先求f′(x),再由f′(-1)=0,可得用含a的代数式表示b,这时f(x)中只含一个参数a,然后令f′(x)=0,求得两根,通过列表,求得f(x)的单调区间,并注意分类讨论.
解析 (1)依题意,得f′(x)=x2+2ax+b.
由f′(-1)=0,得1-2a+b=0.∴b=2a-1.
(2)由(1),得f(x)=x3+ax2+(2a-1)x.
故f′(x)=x2+2ax+2a-1=(x+1)(x+2a-1).
令f′(x)=0,则x=-1或x=1-2a.
①当a>1时,1-2a<-1.
当x变化时,f′(x)与f(x)的变化情况如下表:
x
(-∞,1-2a)
(1-2a,-1)
(-1,+∞)
f′(x)
+
-
+
f(x)
单调递增
单调递减
单调递增
由此得,函数f(x)的单调增区间为(-∞,1-2a)和(-1,+∞),单调减区间为(1-2a,-1).
②当a=1时,1-2a=-1,此时f′(x)≥0恒成立,且仅在x=-1处f′(x)=0,故函数f(x)的单调增区间为R.
③当a<1时,1-2a>-1,同理可得函数f(x)的单调增区间为(-∞,-1)和(1-2a,+∞),单调减区间(-1,1-2a).
综上:当a>1时,函数f(x)的单调增区间为(-∞,1-2a)和(-1,+∞),单调减区间为(1-2a,-1);
当a=1时,函数f(x)的单调增区间为R;
当a<1时,函数f(x)的单调增区间为(-∞,-1)和(1-2a,+∞),单调减区间为(-1,1-2a).
重点班·选做题
18.设函数f(x)=(x>0且x≠1),求函数f(x)的单调区间;
解析 f′(x)=-.
若f′(x)=0,则x=.
当f′(x)>0,即0当f′(x)<0,即1时,f(x)为减函数.
所以f(x)的单调增区间为(0,),
单调减区间为[,1)和(1,+∞).
函数的单调性与导数
同步练习
一、选择题
1.函数f(x)=2x-sin
x在(-∞,+∞)上( )
A.是增函数
B.是减函数
C.有最大值
D.有最小值
答案 A
2.函数f(x)=5x2-2x的单调递减区间是( )
A.(,+∞)
B.(-∞,)
C.(-,+∞)
D.(-∞,-)
答案 B
3.函数y=xlnx在区间(0,1)上是( )
A.单调增函数
B.单调减函数
C.在(0,)上是减函数,在(,1)上是增函数
D.在(0,)上是增函数,在(,1)上是减函数
答案 C
解析 f′(x)=lnx+1,当0
4.函数y=4x2+的单调增区间为( )
A.(0,+∞)
B.(,+∞)
C.(-∞,-1)
D.(-∞,-)
答案 B
解析 y′=8x-,令y′>0,得8x->0,
即x3>,
∴x>.
5.若函数y=a(x3-x)的递减区间为(-,),则a的取值范围是( )
A.a>0
B.-1<a<0
C.a>1
D.0<a<1
答案 A
解析 y′=a(3x2-1),解3x2-1<0,得-<x<.
∴f(x)=x3-x在(-,)上为减函数.
又y=a·(x3-x)的递减区间为(-,).
∴a>0.
6.
已知f′(x)是f(x)的导函数,y=f′(x)的图像如图所示,则f(x)的图像只可能是( )
答案 D
解析 从y=f′(x)的图像可以看出,在区间(a,)内,导数值递增;在区(,b)内,导数值递减,即函数f(x)的图像在(a,)内越来越陡峭,在(,b)内越来越平缓.
7.函数f(x)=(x-3)ex的单调递增区间是( )
A.(-∞,2)
B.(0,3)
C.(1,4)
D.(2,+∞)
答案 D
解析 f′(x)=ex+(x-3)ex=ex(x-2),
由f′(x)>0,得x>2.∴f(x)在(2,+∞)上是增函数.
二、填空题
8.若函数y=-x3+bx有三个单调区间,则b的取值范围是________.
答案 (0,+∞)
解析 若函数y=-x3+bx有三个单调区间,则其导数y′=-4x2+b=0有两个不相等的实数根,所以b>0.
9.若函数f(x)=x-+在(1,+∞)上是增函数,则实数p的取值范围是________.
答案 [-1,+∞)
解析 f′(x)=1+≥0对x>1恒成立,即x2+p≥0对x>1恒成立,∴p≥-x2(x>1).∴p≥-1.
10.若函数y=ax3-ax2-2ax(a≠0)在[-1,2]上为增函数,则a∈________.
答案 (-∞,0)
解析 y′=ax2-ax-2a=a(x+1)(x-2)>0,
∵当x∈(-1,2)时,(x+1)(x-2)<0,
∴a<0.
11.f(x)=(x∈R)在区间[-1,1]上是增函数,则a∈________.
答案 [-1,1]
解析 y′=2·,
∵f(x)在[-1,1]上是增函数,∴y′在(-1,1)上大于等于0,即2·≥0.
∵(x2+2)2>0,
∴x2-ax-2≤0对x∈(-1,1)恒成立.
令g(x)=x2-ax-2,
则 即 ∴-1≤a≤1.
即a的取值范围是[-1,1].
三、解答题
12.已知f(x)=ax3+3x2-x-1在R上是减函数,求a的取值范围.
解析 ∵f′(x)=3ax2+6x-1,又f(x)在R上递减,
∴f′(x)≤0对x∈R恒成立.
即3ax2+6x-1≤0对x∈R恒成立,显然a≠0.
∴ ∴a≤-3.
即a的取值范围为(-∞,-3].
13.已知函数f(x)=x2+(x≠0,常数a∈R).若函数
f(x)在[2,+∞)上是单调递增的,求a的取值范围.
解析 f′(x)=2x-=,
要使f(x)在[2,+∞)上是单调递增的,
则f′(x)≥0在x∈[2,+∞)时恒成立,
即≥0在x∈[2,+∞)时恒成立.
∵x>0,∴2x3-a≥0,∴a≤2x3在x∈[2,+∞)上恒成立.
∴a≤(2x3)min.
∵x∈[2,+∞),y=2x3是单调递增的,
∴(2x3)min=16,∴a≤16.
当a=16时,
f′(x)=≥0(x∈[2,+∞))有且只有f′(2)=0.
∴a的取值范围是a≤16.
14.已知函数f(x)=x3+ax2+1,a∈R.
(1)讨论函数f(x)的单调区间;
(2)设函数f(x)在区间(-,-)内是减函数,求a的取值范围.
解析 (1)对f(x)求导,得
f′(x)=3x2+2ax=3x(x+a).
①当a=0时,f′(x)=3x2≥0恒成立.
∴f(x)的递增区间是(-∞,+∞);
②当a>0时,由于f′(x)分别在(-∞,-α)和(0,+∞)上都恒为正,所以f(x)的递增区间是(-∞,-a),(0,+∞);由于f′(x)在(-a,0)上恒为负,所以f(x)的递减区间是(-a,0);
③当a<0时,在x∈(-∞,0)和x∈(-a,+∞)上均有f′(x)>0,∴f(x)的递增区间是(-∞,0),(-a,+∞);在(0,-a)上,f′(x)<0,f(x)的递减区间是(0,-a).
(2)由(1)知,(-,-) (-a,0),
∴-a≤-.∴a≥1.
15.若函数f(x)=x3-ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围.
分析 本题主要考查借助函数的单调性来求导的能力及解不等式的能力.
解析 ∵f′(x)=x2-ax+a-1,令f′(x)=0,
解得x=1或x=a-1.
当a-1≤1,即a≤2时,函数f(x)在(1,+∞)上为增函数,不符合题意.
当a-1>1,即a>2时,函数f(x)在(-∞,1)上为增函数,在(1,a-1)上为减函数,在(a-1,+∞)上为增函数.
而当x∈(1,4)时,f′(x)<0;
当x∈(6,+∞)时,f′(x)>0.
∴4≤a-1≤6,即5≤a≤7.
∴a的取值范围是[5,7].
16.已知f(x)=在区间[1,+∞)上是增函数,求实数a的取值范围.
解析 因为f(x)=x-+,所以f′(x)=1+.
又f(x)在[1,+∞)上是增函数,
所以当x∈[1,+∞)时,恒有f′(x)=1+≥0,
即a≥-x2,x∈[1,+∞).所以a≥-1.
故所求a的取值范围是[-1,+∞).
17.已知函数f(x)=x3+ax2+bx,且f′(-1)=0.
(1)试用含a
代数式表示b;
(2)求f(x)的单调区间.
分析 可先求f′(x),再由f′(-1)=0,可得用含a的代数式表示b,这时f(x)中只含一个参数a,然后令f′(x)=0,求得两根,通过列表,求得f(x)的单调区间,并注意分类讨论.
解析 (1)依题意,得f′(x)=x2+2ax+b.
由f′(-1)=0,得1-2a+b=0.∴b=2a-1.
(2)由(1),得f(x)=x3+ax2+(2a-1)x.
故f′(x)=x2+2ax+2a-1=(x+1)(x+2a-1).
令f′(x)=0,则x=-1或x=1-2a.
①当a>1时,1-2a<-1.
当x变化时,f′(x)与f(x)的变化情况如下表:
x
(-∞,1-2a)
(1-2a,-1)
(-1,+∞)
f′(x)
+
-
+
f(x)
单调递增
单调递减
单调递增
由此得,函数f(x)的单调增区间为(-∞,1-2a)和(-1,+∞),单调减区间为(1-2a,-1).
②当a=1时,1-2a=-1,此时f′(x)≥0恒成立,且仅在x=-1处f′(x)=0,故函数f(x)的单调增区间为R.
③当a<1时,1-2a>-1,同理可得函数f(x)的单调增区间为(-∞,-1)和(1-2a,+∞),单调减区间(-1,1-2a).
综上:当a>1时,函数f(x)的单调增区间为(-∞,1-2a)和(-1,+∞),单调减区间为(1-2a,-1);
当a=1时,函数f(x)的单调增区间为R;
当a<1时,函数f(x)的单调增区间为(-∞,-1)和(1-2a,+∞),单调减区间为(-1,1-2a).
重点班·选做题
18.设函数f(x)=(x>0且x≠1),求函数f(x)的单调区间;
解析 f′(x)=-.
若f′(x)=0,则x=.
当f′(x)>0,即0
所以f(x)的单调增区间为(0,),
单调减区间为[,1)和(1,+∞).
