1.5.1 曲边梯形的面积 教案
文档属性
| 名称 | 1.5.1 曲边梯形的面积 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 164.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-15 21:50:12 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.5.1
曲边梯形的面积
教案
一:教学目标
理解求曲边图形面积的过程:分割、以直代曲、逼近,感受在其过程中渗透的思想方法
二:教学重难点
重点
掌握过程步骤:分割、以直代曲、求和、逼近(取极限)
难点
对过程中所包含的基本的微积分
“以直代曲”的思想的理解
三:教学过程:
1.创设情景
我们学过如何求正方形、长方形、三角形等的面积,这些图形都是由直线段围成的.那么,如何求曲线围成的平面图形的面积呢?
这就是定积分要解决的问题.
定积分在科学研究和实际生活中都有非常广泛的应用.本节我们将学习定积分的基本概念以及定积分的简单应用,初步体会定积分的思想及其应用价值.www.21-cn-jy.com
一个概念:如果函数在某一区间上的图像是一条连续不断的曲线,那么就把函数称为区间上的连续函数.(不加说明,下面研究的都是连续函数)2·1·c·n·j·y
2.新课讲授
问题:如图,阴影部分类似于一个梯形,但有一边是曲线的一段,我们把由直线和曲线所围成的图形称为曲边梯形.如何计算这个曲边梯形的面积?
【来源:21·世纪·教育·网】
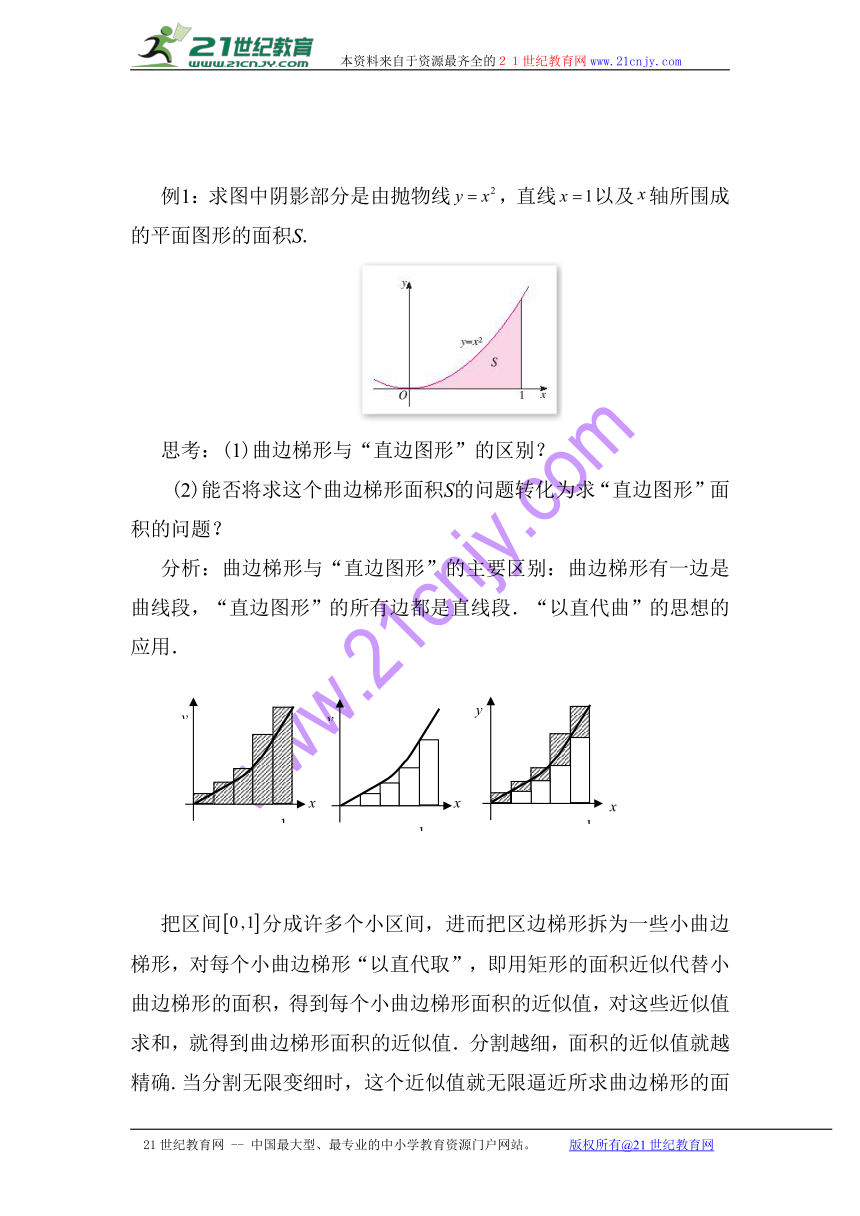
例1:求图中阴影部分是由抛物线,直线以及轴所围成的平面图形的面积S.
思考:(1)曲边梯形与“直边图形”的区别?
(2)能否将求这个曲边梯形面积S的问题转化为求“直边图形”面积的问题?
分析:曲边梯形与“直边图形”的主要区别:曲边梯形有一边是曲线段,“直边图形”的所有边都是直线段.“以直代曲”的思想的应用.21教育网
把区间分成许多个小区间,进而把区边梯形拆为一些小曲边梯形,对每个小曲边梯形“以直代取”,即用矩形的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的近似值,对这些近似值求和,就得到曲边梯形面积的近似值.分割越细,面积的近似值就越精确.当分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S.也即:用划归为计算矩形面积和逼近的思想方法求出曲边梯形的面积.21·cn·jy·com
解:
(1).分割
在区间上等间隔地插入个点,将区间等分成个小区间:
,,…,
记第个区间为,其长度为
分别过上述个分点作轴的垂线,从而得到个小曲边梯形,他们的面积分别记作:
,,…,
显然,
(2)近似代替
记,如图所示,当很大,即很小时,在区间上,可以认为函数的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点处的函数值,从图形上看,就是用平行于轴的直线段近似的代替小曲边梯形的曲边(如图).这样,在区间上,用小矩形的面积近似的代替,即在局部范围内“以直代取”,则有21cnjy.com
(3)求和
因为每个小矩形的面积是相应的小曲边梯形面积的近似值,所以个小矩形面积之和就是所求曲边三角形面积的近似值:
=
(4)取极限
当分割无限变细时,即无限趋近于(趋向于)
当趋向时,无限趋近于,无限趋近于,故上式的结果无限趋近于,,即所求曲边三角形面积是.
从数值上的变化趋势:
3.求曲边梯形面积的四个步骤:
第一步:分割.在区间中任意插入各分点,将它们等分成个小区间,区间的长度,
第二步:近似代替,“以直代取”.用矩形的面积近似代替小曲边梯形的面积,求出每个小曲边梯形面积的近似值.21世纪教育网版权所有
第三步:求和.
第四步:取极限.
说明:1.归纳以上步骤,其流程图表示为:
分割以直代曲求和逼近
2.最后所得曲边形的面积不是近似值,而是真实值
例2.
求由直线y=2x+1与直线x=0,x=1和y=0所围成的平面图形的面积S.
【解】(1)分割
在区间
[0,1]上等间隔地插入n-1个点,将它等分成n个小区间:
分别过上述n-1个分点作垂线,把曲边梯形分成n个小曲边梯形.它们的面积记作
(2)近似代替
记f(x)=2x+1,当n很大时,第i个小曲边梯形的面积
可以用小矩形(以为底,为高)的面积近似代替,则有:
(3)求和
(4)取极限
当n趋向于无穷大时,趋向于S,从而有:
S=
4.课堂小结:
5.教学后记:
x
x
x
1
x
1
x
y
1
x
y
y
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
1.5.1
曲边梯形的面积
教案
一:教学目标
理解求曲边图形面积的过程:分割、以直代曲、逼近,感受在其过程中渗透的思想方法
二:教学重难点
重点
掌握过程步骤:分割、以直代曲、求和、逼近(取极限)
难点
对过程中所包含的基本的微积分
“以直代曲”的思想的理解
三:教学过程:
1.创设情景
我们学过如何求正方形、长方形、三角形等的面积,这些图形都是由直线段围成的.那么,如何求曲线围成的平面图形的面积呢?
这就是定积分要解决的问题.
定积分在科学研究和实际生活中都有非常广泛的应用.本节我们将学习定积分的基本概念以及定积分的简单应用,初步体会定积分的思想及其应用价值.www.21-cn-jy.com
一个概念:如果函数在某一区间上的图像是一条连续不断的曲线,那么就把函数称为区间上的连续函数.(不加说明,下面研究的都是连续函数)2·1·c·n·j·y
2.新课讲授
问题:如图,阴影部分类似于一个梯形,但有一边是曲线的一段,我们把由直线和曲线所围成的图形称为曲边梯形.如何计算这个曲边梯形的面积?
【来源:21·世纪·教育·网】
例1:求图中阴影部分是由抛物线,直线以及轴所围成的平面图形的面积S.
思考:(1)曲边梯形与“直边图形”的区别?
(2)能否将求这个曲边梯形面积S的问题转化为求“直边图形”面积的问题?
分析:曲边梯形与“直边图形”的主要区别:曲边梯形有一边是曲线段,“直边图形”的所有边都是直线段.“以直代曲”的思想的应用.21教育网
把区间分成许多个小区间,进而把区边梯形拆为一些小曲边梯形,对每个小曲边梯形“以直代取”,即用矩形的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的近似值,对这些近似值求和,就得到曲边梯形面积的近似值.分割越细,面积的近似值就越精确.当分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S.也即:用划归为计算矩形面积和逼近的思想方法求出曲边梯形的面积.21·cn·jy·com
解:
(1).分割
在区间上等间隔地插入个点,将区间等分成个小区间:
,,…,
记第个区间为,其长度为
分别过上述个分点作轴的垂线,从而得到个小曲边梯形,他们的面积分别记作:
,,…,
显然,
(2)近似代替
记,如图所示,当很大,即很小时,在区间上,可以认为函数的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点处的函数值,从图形上看,就是用平行于轴的直线段近似的代替小曲边梯形的曲边(如图).这样,在区间上,用小矩形的面积近似的代替,即在局部范围内“以直代取”,则有21cnjy.com
(3)求和
因为每个小矩形的面积是相应的小曲边梯形面积的近似值,所以个小矩形面积之和就是所求曲边三角形面积的近似值:
=
(4)取极限
当分割无限变细时,即无限趋近于(趋向于)
当趋向时,无限趋近于,无限趋近于,故上式的结果无限趋近于,,即所求曲边三角形面积是.
从数值上的变化趋势:
3.求曲边梯形面积的四个步骤:
第一步:分割.在区间中任意插入各分点,将它们等分成个小区间,区间的长度,
第二步:近似代替,“以直代取”.用矩形的面积近似代替小曲边梯形的面积,求出每个小曲边梯形面积的近似值.21世纪教育网版权所有
第三步:求和.
第四步:取极限.
说明:1.归纳以上步骤,其流程图表示为:
分割以直代曲求和逼近
2.最后所得曲边形的面积不是近似值,而是真实值
例2.
求由直线y=2x+1与直线x=0,x=1和y=0所围成的平面图形的面积S.
【解】(1)分割
在区间
[0,1]上等间隔地插入n-1个点,将它等分成n个小区间:
分别过上述n-1个分点作垂线,把曲边梯形分成n个小曲边梯形.它们的面积记作
(2)近似代替
记f(x)=2x+1,当n很大时,第i个小曲边梯形的面积
可以用小矩形(以为底,为高)的面积近似代替,则有:
(3)求和
(4)取极限
当n趋向于无穷大时,趋向于S,从而有:
S=
4.课堂小结:
5.教学后记:
x
x
x
1
x
1
x
y
1
x
y
y
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
