1.6 微积分基本定理 教案
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.6
微积分基本定理
教案
一:教学目标
知识与技能目标
通过实例,直观了解微积分基本定理的含义,会用牛顿-莱布尼兹公式求简单的定积分
过程与方法
通过实例体会用微积分基本定理求定积分的方法
情感态度与价值观
通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力.
二:教学重难点
重点通过探究变速直线运动物体的速度与位移的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分.21世纪教育网版权所有
难点 了解微积分基本定理的含义
三:教学过程:
复习:
定积分的概念及用定义计算
引入新课
我们讲过用定积分定义计算定积分,但其计算过程比较复杂,所以不是求定积分的一般方法.我们必须寻求计算定积分的新方法,也是比较一般的方法.21cnjy.com
变速直线运动中位置函数与速度函数之间的联系
设一物体沿直线作变速运动,在时刻t时物体所在位置为S(t),速度为v(t)(),
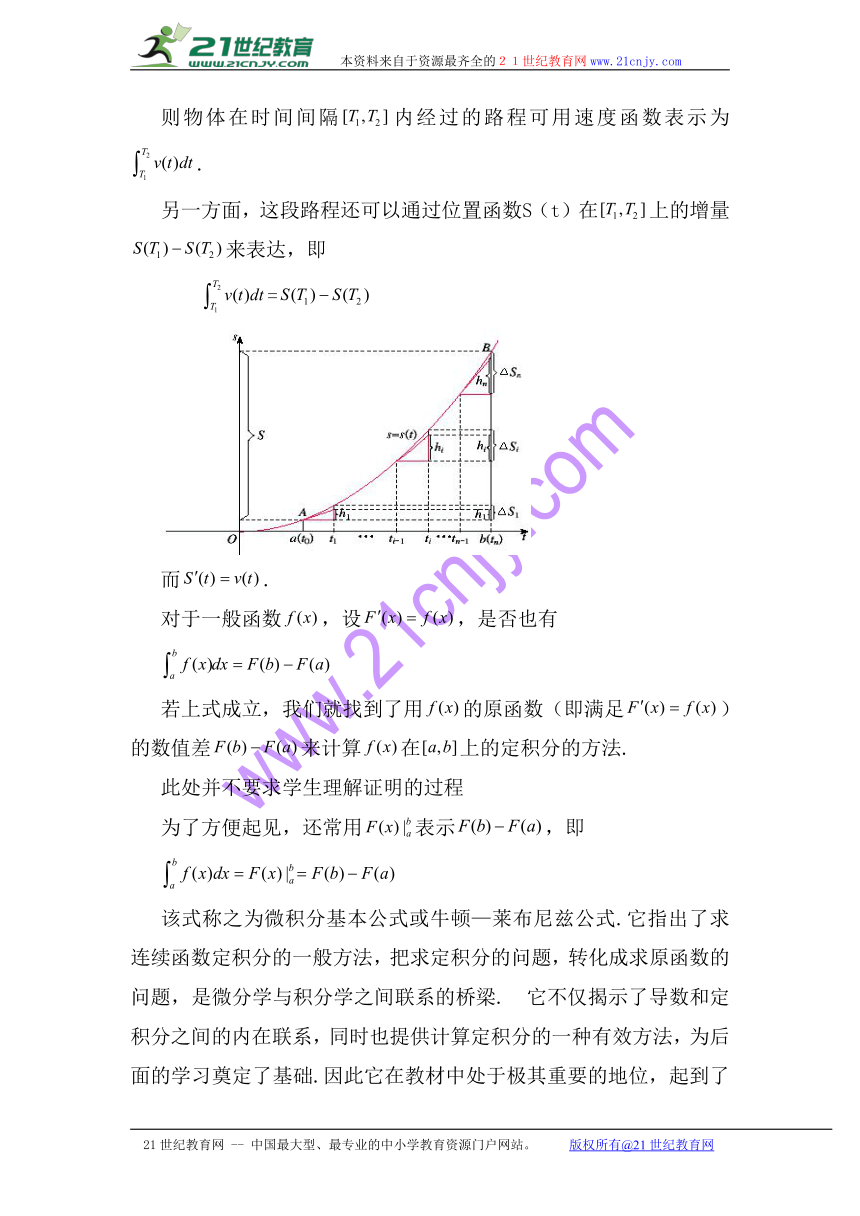
则物体在时间间隔内经过的路程可用速度函数表示为.
另一方面,这段路程还可以通过位置函数S(t)在上的增量来表达,即
=
而.
对于一般函数,设,是否也有
若上式成立,我们就找到了用的原函数(即满足)的数值差来计算在上的定积分的方法.
此处并不要求学生理解证明的过程
为了方便起见,还常用表示,即
该式称之为微积分基本公式或牛顿—莱布尼兹公式.它指出了求连续函数定积分的一般方法,把求定积分的问题,转化成求原函数的问题,是微分学与积分学之间联系的桥梁.
它不仅揭示了导数和定积分之间的内在联系,同时也提供计算定积分的一种有效方法,为后面的学习奠定了基础.因此它在教材中处于极其重要的地位,起到了承上启下的作用,不仅如此,它甚至给微积分学的发展带来了深远的影响,是微积分学中最重要最辉煌的成果.21·cn·jy·com
例1.计算下列定积分:
(1);
(2).
解:(1)因为,
所以.
(2))因为,
所以
.
练习:计算
解:由于是的一个原函数,所以根据牛顿—莱布尼兹公式有
===
可以发现,定积分的值可能取正值也可能取负值,还可能是0:
(1)当对应的曲边梯形位于
x
轴上方时,定积分的值取正值,且等于曲边梯形的面积;
(2)当对应的曲边梯形位于
x
轴下方时,定积分的值取负值,且等于曲边梯形的面积的相反数;
(
3)当位于
x
轴上方的曲边梯形面积等于位于
x
轴下方的曲边梯形面积时,定积分的值为0
,且等于位于
x
轴上方的曲边梯形面积减去位于
x
轴下方的曲边梯形面积.
21教育网
课堂小结:
本节课借助于变速运动物体的速度与路程的关系以及图形得出了特殊情况下的牛顿-莱布尼兹公式.成立,进而推广到了一般的函数,得出了微积分基本定理,得到了一种求定积分的简便方法,运用这种方法的关键是找到被积函数的原函数,这就要求大家前面的求导数的知识比较熟练,希望,不明白的同学,回头来多复习!
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
1.6
微积分基本定理
教案
一:教学目标
知识与技能目标
通过实例,直观了解微积分基本定理的含义,会用牛顿-莱布尼兹公式求简单的定积分
过程与方法
通过实例体会用微积分基本定理求定积分的方法
情感态度与价值观
通过微积分基本定理的学习,体会事物间的相互转化、对立统一的辩证关系,培养学生辩证唯物主义观点,提高理性思维能力.
二:教学重难点
重点通过探究变速直线运动物体的速度与位移的关系,使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分.21世纪教育网版权所有
难点 了解微积分基本定理的含义
三:教学过程:
复习:
定积分的概念及用定义计算
引入新课
我们讲过用定积分定义计算定积分,但其计算过程比较复杂,所以不是求定积分的一般方法.我们必须寻求计算定积分的新方法,也是比较一般的方法.21cnjy.com
变速直线运动中位置函数与速度函数之间的联系
设一物体沿直线作变速运动,在时刻t时物体所在位置为S(t),速度为v(t)(),
则物体在时间间隔内经过的路程可用速度函数表示为.
另一方面,这段路程还可以通过位置函数S(t)在上的增量来表达,即
=
而.
对于一般函数,设,是否也有
若上式成立,我们就找到了用的原函数(即满足)的数值差来计算在上的定积分的方法.
此处并不要求学生理解证明的过程
为了方便起见,还常用表示,即
该式称之为微积分基本公式或牛顿—莱布尼兹公式.它指出了求连续函数定积分的一般方法,把求定积分的问题,转化成求原函数的问题,是微分学与积分学之间联系的桥梁.
它不仅揭示了导数和定积分之间的内在联系,同时也提供计算定积分的一种有效方法,为后面的学习奠定了基础.因此它在教材中处于极其重要的地位,起到了承上启下的作用,不仅如此,它甚至给微积分学的发展带来了深远的影响,是微积分学中最重要最辉煌的成果.21·cn·jy·com
例1.计算下列定积分:
(1);
(2).
解:(1)因为,
所以.
(2))因为,
所以
.
练习:计算
解:由于是的一个原函数,所以根据牛顿—莱布尼兹公式有
===
可以发现,定积分的值可能取正值也可能取负值,还可能是0:
(1)当对应的曲边梯形位于
x
轴上方时,定积分的值取正值,且等于曲边梯形的面积;
(2)当对应的曲边梯形位于
x
轴下方时,定积分的值取负值,且等于曲边梯形的面积的相反数;
(
3)当位于
x
轴上方的曲边梯形面积等于位于
x
轴下方的曲边梯形面积时,定积分的值为0
,且等于位于
x
轴上方的曲边梯形面积减去位于
x
轴下方的曲边梯形面积.
21教育网
课堂小结:
本节课借助于变速运动物体的速度与路程的关系以及图形得出了特殊情况下的牛顿-莱布尼兹公式.成立,进而推广到了一般的函数,得出了微积分基本定理,得到了一种求定积分的简便方法,运用这种方法的关键是找到被积函数的原函数,这就要求大家前面的求导数的知识比较熟练,希望,不明白的同学,回头来多复习!
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
