1.7.3 定积分 同步练习(含答案)
文档属性
| 名称 | 1.7.3 定积分 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 253.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-16 00:00:00 | ||
图片预览




文档简介
1.7.3
定积分
同步练习
一、选择题
1.
下列表示图中f(x)在区间[a,b]的图像与x轴围成的面积总和的式子中,正确的是( )
A.f(x)dx
B.
C.f(x)dx+f(x)dx+f(x)dx
D.f(x)dx-f(x)dx+f(x)dx
答案 D
2.若(2x+)dx=3+ln2,则a的值是( )
A.6
B.4
C.3
D.2
答案 D
3.f(x)是一次函数,且f(x)dx=5,xf(x)dx=,那么f(x)的解析式是( )
A.4x+3
B.3x+4
C.-4x+2
D.-3x+4
答案 A
解析 设y=kx+b(k≠0),(kx+b)dx=(kx2+bx)|=k+b=5,①
x(kx+b)dx=(kx3+bx2)|=,
得k+b=.②
解①②得
4.下列各式中正确的是( )
A.B.C.D.0答案 B
解析 图解如图由几何性可知选B.
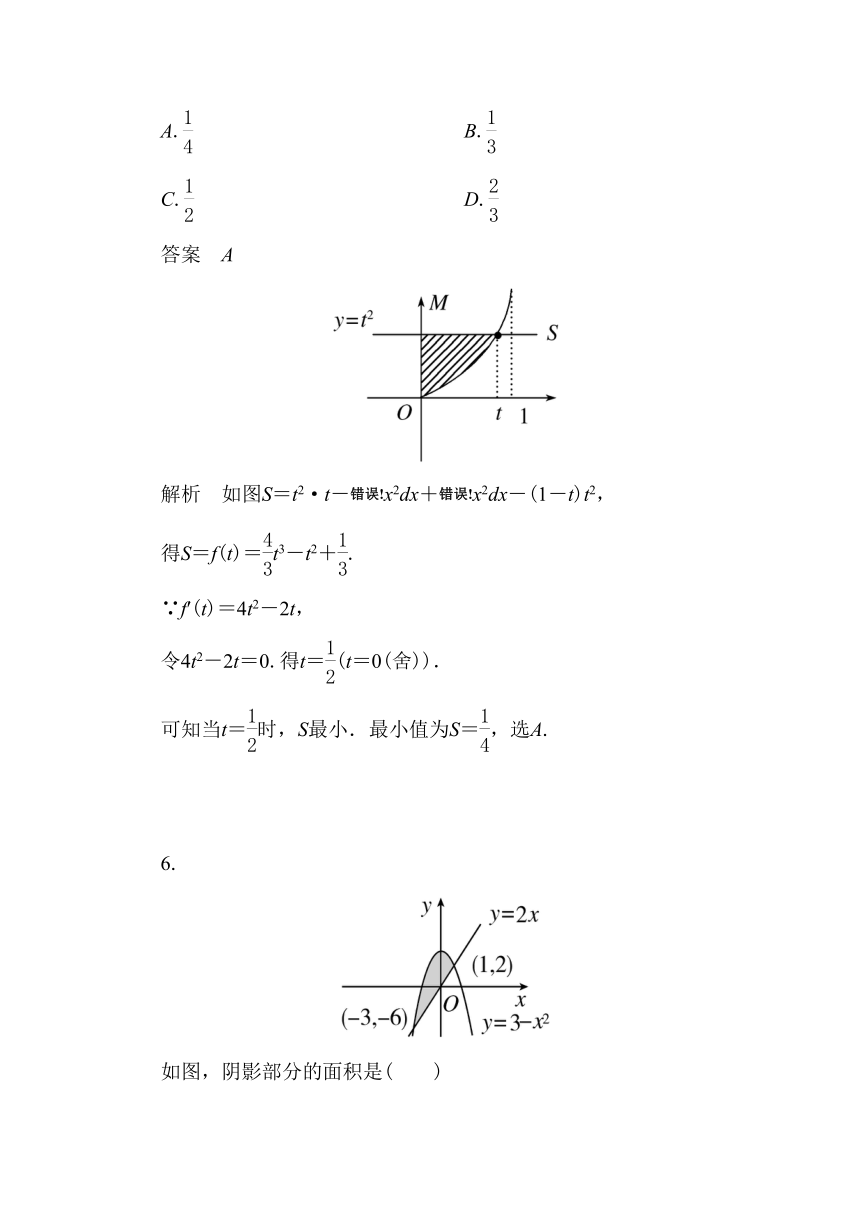
5.由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形的面积的最小值为( )
A.
B.
C.
D.
答案 A
解析 如图S=t2·t-x2dx+x2dx-(1-t)t2,
得S=f(t)=t3-t2+.
∵f′(t)=4t2-2t,
令4t2-2t=0.得t=(t=0(舍)).
可知当t=时,S最小.最小值为S=,选A.
6.
如图,阴影部分的面积是( )
A.2
B.-2
C.
D.
答案 C
7.由直线x=,x=2,曲线y=及x轴所围图形的面积为( )
A.
B.
C.ln2
D.2ln2
答案 D
8.在下面所给图形的面积S及相应表达式中,正确的有( )
S=[g(x)-f(x)]dx
S=(2x-2x+8)dx
①
②
S=f(x)dx-f(x)dx
S=[g(x)-f(x)]dx+[f(x)-g(x)]dx
③
④
A.①③
B.②③
C.①④
D.③④
答案 D
解析 ①应是S=[f(x)-g(x)]dx,
②应是S=2dx-(2x-8)dx,
③和④正确.故选D.
二、填空题
9.若x(a-x)dx=2,则实数a=________.
答案
10.设f(x)是连续函数,且f(x)=x+2f
(t)dt,则f(x)=_______.
答案 x-2
11.设函数f(x)=ax2+c(a≠0),若f(x)dx=f(x0),(0≤x0≤1),则x0的值为________.
答案
三、解答题
12.(|2-x|+|sinx)|dx.
解析 原式=(|x-2|)dx+(|sinx|)dx
=+2+sinxdx+(-sinx)dx
=+2+2+cos5+1=+cos5.
13.已知f(x)是一个一次函数,其图像过(3,4),且f(x)dx=1,求f(x)的解析式.
解析 设f(x)=kx+b(k≠0),其图像过点(3,4),
∴4=3k+b.
1=(kx+b)dx=(kx2+bx)|=k+b.
从而有解得
∴f(x)=x+.
重点班·选做题
14.求c的值,使(x2+cx+c)2dx最小.
解析 令y=(x2+cx+c)2dx
=(x4+2cx3+c2x2+2cx2+2c2x+c2)dx
=(x5+cx4+c2x3+cx3+c2x2+c2x)
=+c+c2,令y′=c+=0,
得c=-,所以当c=-时,y最小.
教师备选题
1.从空中自由下落的物体,在第一秒时刻恰经过电视塔顶,在第2秒时刻物体落地,已知自由落体的运动速度为v=gt(g为常数),则电视塔高为________.
答案 g
2.在曲线y=x2(x≥0)上某一点A处作一切线与曲线及坐标轴所围成图形的面积为,试求:
(1)过点A的坐标;
(2)过切点A的切线方程.
解析 如图所示,设切点A(x0,y0).
由y′=2x知过A点切线方程为y-y0=2x0(x-x0)且y0=x,
即y=2x0x-x.
令y=0,得C(,0).
设由曲线与过A点的切线及x轴围成的面积为S,则S=S曲线OAB-S△ABC=.
∵S曲边AOB=x2dx=x3=x,
S△ABC=BC·AB=(x0-)·x=x,
∴=x-x=.
解得x0=1,从而A(1,1)切线方程为y=2x-1.
3.
A,B两站相距7.2
km,一辆电车从A站开往B站,电车开出t
s后到达途中C点,这一段速度为1.2t(m/s),到达C的速度达24
m/s,从C点到B点前的D点匀速行驶,从D点开始刹车,经t
s后,速度为(24-1.2t)m/s,在B处恰好停车,试求:
(1)A,C间的距离;
(2)B,D间的距离;
(3)从A到B的时间.
解析 (1)设A到C点经过t1s,
由1.2t1=24,得t1=20(s).
∴AC=1.2tdt=0.6t2=240
(m).
(2)设从D→B经过t2s,
由24-1.2t2=0,得t2=20(s).
∴DB=(24-1.2t)dt=(24t-0.6t2)=240(m).
从C到D的时间t3==280(s),
所求A到B的时间为20+280+20=320(s).
走向高考
1.如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
A.
B.
C.
D.
答案 C
解析 利用积分求出阴影部分的面积,应用几何概型的概率计算公式求解.
∵S阴影=(-x)dx=(x-x2)=-=,又S正方形OABC=1,∴由几何概型知,P恰好取自阴影部分的概率为=.
2.曲线y=-在点M(,0)处的切线的斜率为( )
A.-
B.
C.-
D.
答案 B
解析 y′=
=,故y′x==,
∴曲线在点M(,0)处的切线的斜率为.
3.若f(x)=x2-2x-4lnx,则f′(x)>0的解集为( )
A.(0,+∞)
B.(-1,0)∪(2,+∞)
C.(2,+∞)
D.(-1,0)
答案 C
解析 由题意知x>0,且f′(x)=2x-2-,
即f′(x)=>0,∴x2-x-2>0,
解得x<-1或x>2.又∵x>0,∴x>2.
4.由曲线y=,直线y=x-2及y轴所围成的图形的面积为( )
A.
B.4
C.
D.6
答案 C
解析 由得其交点坐标为(4,2).
因此y=与y=x-2及y轴所围成的图形的面积为
[-(x-2)]dx=(-x+2)dx
=(x-x2+2x)=×8-×16+2×4=.
5.函数y=-2sinx的图像大致是( )
答案 C
解析 因为y=-2sinx是奇函数,所以其图像关于原点对称,因此可排除A.为求解本题,应先研究=2sinx,即sinx=x,在同一坐标系内作出y1=sinx与y2=x的图像,如下图,可知,当x>0时,y1=sinx与y2=x只有一个交点,设其交点坐标为(x0,y0),则当x∈(0,x0)时,sinx>x,即2sinx>x,此时,y=x-2sinx<0.又f′(x)=-2cosx,因此当x>0时,可以有f′(x)>0,也可以有f′(x)<0,即函数有增有减,有多个极值点,且极值点呈周期性,因此可排除B、D,故选C.
6.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )
A.13万件
B.11万件
C.9万件
D.7万件
答案 C
解析 ∵y=f(x)=-x3+81x-234,
∴y′=-x2+81.
令y′=0,得x=9,x=-9(舍去).
当00,函数f(x)单调递增;
当x>9时,y′<0,函数f(x)单调递减.
故当x=9时,y取最大值.
7.已知点P在曲线y=上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )
A.[0,)
B.[,)
C.(,]
D.[,π)
答案 D
解析 ∵y=,∴y′=.
令ex+1=t,则ex=t-1且t>1.
∴y′==-.
再令=m,则0∴y′=4m2-4m=4(m-)2-1,m∈(0,1).
容易求得-1≤y′<0,∴-1≤tanα<0,得π≤α<π.
8.曲线y=x(3lnx+1)在点(1,1)处的切线方程为________.
答案 y=4x-3
解析 利用导数的几何意义先求得切线斜率.
∵y=x(3lnx+1),∴y′=3lnx+1+x·=3lnx+4.
∴k=y′|x=1=4.
∴所求切线的方程为y-1=4(x-1),即y=4x-3.
9.设a>0,若曲线y=与直线x=a,y=0所围成封闭图形的面积为a2,则a=________.
答案
10.函数f(x)=x3-3x2+1在x=________处取得极小值.
答案 2
解析 由f(x)=x3-3x2+1,可得f′(x)=3x2-6x=
3x(x-2).
当x∈(0,2)时,f′(x)<0,f(x)为减函数,当x∈(-∞,0)∪(2,+∞)时,f′(x)>0,f(x)为增函数,故当x=2时,函数f(x)取得极小值.
11.已知函数f(x)=(x-k)2e.
(1)求f(x)的单调区间;
(2)若对于任意的x∈(0,+∞),都有f(x)≤,求k的取值范围.
解析 (1)f′(x)=(x2-k2)e.
令f′(x)=0,得x=±k.
当k>0时,f(x)与f′(x)的变化情况如下:
x
(-∞,-k)
-k
(-k,k)
k
(k,+∞)
f′(x)
+
0
-
0
+
f(x)
?
4k2e-1
↘
0
?
所以,f(x)的单调递增区间是(-∞,-k)和(k,+∞);单调递减区间是(-k,k).
当k<0时,f(x)与f′(x)的变化情况如下:
x
(-∞,k)
k
(k,-k)
-k
(-k,+∞)
f′(x)
-
0
+
0
-
f(x)
↘
0
?
4k2e-1
↘
所以,f(x)的单调递减区间是(-∞,k)和(-k,+∞);单调递增区间是(k,-k).
(2)当k>0时,因为f(k+1)=e>,所以不会有
x∈(0,+∞),f(x)≤.
当k<0时,由①知f(x)在(0,+∞)上的最大值是
f(-k)=.
所以 x∈(0,+∞),f(x)≤等价于f(-k)=≤.解得-≤k<0.
故当 x∈(0,+∞),f(x)≤时,k的取值范围是[-,0).
教师备选题
1.设f(x)=ln(x+1)++ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y=x在(0,0)点相切.
(1)求a,b的值;
(2)证明:当0解析 (1)由y=f(x)过(0,0)点,得b=-1.
由y=f(x)在(0,0)点的切线斜率为,
又y′|x=0=(++a)|x=0=+a,
得a=0.
(2)证法一 由均值不等式,当x>0时,2记h(x)=f(x)-,则
h′(x)=+-
=-
<-
=.
令g(x)=(x+6)3-216(x+1),则当0g′(x)=3(x+6)2-216<0.
因此g(x)在(0,2)内是递减函数,又由g(0)=0,得
g(x)<0,所以h′(x)<0.
因此h(x)在(0,2)内是递减函数,
又h(0)=0,得h(x)<0.于是
当0证法二 由(1)知f(x)=ln(x+1)+-1.
由均值不等式,当x>0时,
2令k(x)=ln(x+1)-x,则k(0)=0,k′(x)=-1=<0.
故k(x)<0,即ln(x+1)由①②,得当x>0时,f(x)记h(x)=(x+6)f(x)-9x,则当0h′(x)=f(x)+(x+6)f′(x)-9
=[3x(x+1)+(x+6)(2+)-18(x+1)]
<[3x(x+1)+(x+6)(3+)-18(x+1)]
=(7x-18)<0.
因此h(x)在(0,2)内单调递减,又h(0)=0,
所以h(x)<0,即f(x)<.
定积分
同步练习
一、选择题
1.
下列表示图中f(x)在区间[a,b]的图像与x轴围成的面积总和的式子中,正确的是( )
A.f(x)dx
B.
C.f(x)dx+f(x)dx+f(x)dx
D.f(x)dx-f(x)dx+f(x)dx
答案 D
2.若(2x+)dx=3+ln2,则a的值是( )
A.6
B.4
C.3
D.2
答案 D
3.f(x)是一次函数,且f(x)dx=5,xf(x)dx=,那么f(x)的解析式是( )
A.4x+3
B.3x+4
C.-4x+2
D.-3x+4
答案 A
解析 设y=kx+b(k≠0),(kx+b)dx=(kx2+bx)|=k+b=5,①
x(kx+b)dx=(kx3+bx2)|=,
得k+b=.②
解①②得
4.下列各式中正确的是( )
A.
解析 图解如图由几何性可知选B.
5.由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形的面积的最小值为( )
A.
B.
C.
D.
答案 A
解析 如图S=t2·t-x2dx+x2dx-(1-t)t2,
得S=f(t)=t3-t2+.
∵f′(t)=4t2-2t,
令4t2-2t=0.得t=(t=0(舍)).
可知当t=时,S最小.最小值为S=,选A.
6.
如图,阴影部分的面积是( )
A.2
B.-2
C.
D.
答案 C
7.由直线x=,x=2,曲线y=及x轴所围图形的面积为( )
A.
B.
C.ln2
D.2ln2
答案 D
8.在下面所给图形的面积S及相应表达式中,正确的有( )
S=[g(x)-f(x)]dx
S=(2x-2x+8)dx
①
②
S=f(x)dx-f(x)dx
S=[g(x)-f(x)]dx+[f(x)-g(x)]dx
③
④
A.①③
B.②③
C.①④
D.③④
答案 D
解析 ①应是S=[f(x)-g(x)]dx,
②应是S=2dx-(2x-8)dx,
③和④正确.故选D.
二、填空题
9.若x(a-x)dx=2,则实数a=________.
答案
10.设f(x)是连续函数,且f(x)=x+2f
(t)dt,则f(x)=_______.
答案 x-2
11.设函数f(x)=ax2+c(a≠0),若f(x)dx=f(x0),(0≤x0≤1),则x0的值为________.
答案
三、解答题
12.(|2-x|+|sinx)|dx.
解析 原式=(|x-2|)dx+(|sinx|)dx
=+2+sinxdx+(-sinx)dx
=+2+2+cos5+1=+cos5.
13.已知f(x)是一个一次函数,其图像过(3,4),且f(x)dx=1,求f(x)的解析式.
解析 设f(x)=kx+b(k≠0),其图像过点(3,4),
∴4=3k+b.
1=(kx+b)dx=(kx2+bx)|=k+b.
从而有解得
∴f(x)=x+.
重点班·选做题
14.求c的值,使(x2+cx+c)2dx最小.
解析 令y=(x2+cx+c)2dx
=(x4+2cx3+c2x2+2cx2+2c2x+c2)dx
=(x5+cx4+c2x3+cx3+c2x2+c2x)
=+c+c2,令y′=c+=0,
得c=-,所以当c=-时,y最小.
教师备选题
1.从空中自由下落的物体,在第一秒时刻恰经过电视塔顶,在第2秒时刻物体落地,已知自由落体的运动速度为v=gt(g为常数),则电视塔高为________.
答案 g
2.在曲线y=x2(x≥0)上某一点A处作一切线与曲线及坐标轴所围成图形的面积为,试求:
(1)过点A的坐标;
(2)过切点A的切线方程.
解析 如图所示,设切点A(x0,y0).
由y′=2x知过A点切线方程为y-y0=2x0(x-x0)且y0=x,
即y=2x0x-x.
令y=0,得C(,0).
设由曲线与过A点的切线及x轴围成的面积为S,则S=S曲线OAB-S△ABC=.
∵S曲边AOB=x2dx=x3=x,
S△ABC=BC·AB=(x0-)·x=x,
∴=x-x=.
解得x0=1,从而A(1,1)切线方程为y=2x-1.
3.
A,B两站相距7.2
km,一辆电车从A站开往B站,电车开出t
s后到达途中C点,这一段速度为1.2t(m/s),到达C的速度达24
m/s,从C点到B点前的D点匀速行驶,从D点开始刹车,经t
s后,速度为(24-1.2t)m/s,在B处恰好停车,试求:
(1)A,C间的距离;
(2)B,D间的距离;
(3)从A到B的时间.
解析 (1)设A到C点经过t1s,
由1.2t1=24,得t1=20(s).
∴AC=1.2tdt=0.6t2=240
(m).
(2)设从D→B经过t2s,
由24-1.2t2=0,得t2=20(s).
∴DB=(24-1.2t)dt=(24t-0.6t2)=240(m).
从C到D的时间t3==280(s),
所求A到B的时间为20+280+20=320(s).
走向高考
1.如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
A.
B.
C.
D.
答案 C
解析 利用积分求出阴影部分的面积,应用几何概型的概率计算公式求解.
∵S阴影=(-x)dx=(x-x2)=-=,又S正方形OABC=1,∴由几何概型知,P恰好取自阴影部分的概率为=.
2.曲线y=-在点M(,0)处的切线的斜率为( )
A.-
B.
C.-
D.
答案 B
解析 y′=
=,故y′x==,
∴曲线在点M(,0)处的切线的斜率为.
3.若f(x)=x2-2x-4lnx,则f′(x)>0的解集为( )
A.(0,+∞)
B.(-1,0)∪(2,+∞)
C.(2,+∞)
D.(-1,0)
答案 C
解析 由题意知x>0,且f′(x)=2x-2-,
即f′(x)=>0,∴x2-x-2>0,
解得x<-1或x>2.又∵x>0,∴x>2.
4.由曲线y=,直线y=x-2及y轴所围成的图形的面积为( )
A.
B.4
C.
D.6
答案 C
解析 由得其交点坐标为(4,2).
因此y=与y=x-2及y轴所围成的图形的面积为
[-(x-2)]dx=(-x+2)dx
=(x-x2+2x)=×8-×16+2×4=.
5.函数y=-2sinx的图像大致是( )
答案 C
解析 因为y=-2sinx是奇函数,所以其图像关于原点对称,因此可排除A.为求解本题,应先研究=2sinx,即sinx=x,在同一坐标系内作出y1=sinx与y2=x的图像,如下图,可知,当x>0时,y1=sinx与y2=x只有一个交点,设其交点坐标为(x0,y0),则当x∈(0,x0)时,sinx>x,即2sinx>x,此时,y=x-2sinx<0.又f′(x)=-2cosx,因此当x>0时,可以有f′(x)>0,也可以有f′(x)<0,即函数有增有减,有多个极值点,且极值点呈周期性,因此可排除B、D,故选C.
6.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )
A.13万件
B.11万件
C.9万件
D.7万件
答案 C
解析 ∵y=f(x)=-x3+81x-234,
∴y′=-x2+81.
令y′=0,得x=9,x=-9(舍去).
当0
当x>9时,y′<0,函数f(x)单调递减.
故当x=9时,y取最大值.
7.已知点P在曲线y=上,α为曲线在点P处的切线的倾斜角,则α的取值范围是( )
A.[0,)
B.[,)
C.(,]
D.[,π)
答案 D
解析 ∵y=,∴y′=.
令ex+1=t,则ex=t-1且t>1.
∴y′==-.
再令=m,则0
容易求得-1≤y′<0,∴-1≤tanα<0,得π≤α<π.
8.曲线y=x(3lnx+1)在点(1,1)处的切线方程为________.
答案 y=4x-3
解析 利用导数的几何意义先求得切线斜率.
∵y=x(3lnx+1),∴y′=3lnx+1+x·=3lnx+4.
∴k=y′|x=1=4.
∴所求切线的方程为y-1=4(x-1),即y=4x-3.
9.设a>0,若曲线y=与直线x=a,y=0所围成封闭图形的面积为a2,则a=________.
答案
10.函数f(x)=x3-3x2+1在x=________处取得极小值.
答案 2
解析 由f(x)=x3-3x2+1,可得f′(x)=3x2-6x=
3x(x-2).
当x∈(0,2)时,f′(x)<0,f(x)为减函数,当x∈(-∞,0)∪(2,+∞)时,f′(x)>0,f(x)为增函数,故当x=2时,函数f(x)取得极小值.
11.已知函数f(x)=(x-k)2e.
(1)求f(x)的单调区间;
(2)若对于任意的x∈(0,+∞),都有f(x)≤,求k的取值范围.
解析 (1)f′(x)=(x2-k2)e.
令f′(x)=0,得x=±k.
当k>0时,f(x)与f′(x)的变化情况如下:
x
(-∞,-k)
-k
(-k,k)
k
(k,+∞)
f′(x)
+
0
-
0
+
f(x)
?
4k2e-1
↘
0
?
所以,f(x)的单调递增区间是(-∞,-k)和(k,+∞);单调递减区间是(-k,k).
当k<0时,f(x)与f′(x)的变化情况如下:
x
(-∞,k)
k
(k,-k)
-k
(-k,+∞)
f′(x)
-
0
+
0
-
f(x)
↘
0
?
4k2e-1
↘
所以,f(x)的单调递减区间是(-∞,k)和(-k,+∞);单调递增区间是(k,-k).
(2)当k>0时,因为f(k+1)=e>,所以不会有
x∈(0,+∞),f(x)≤.
当k<0时,由①知f(x)在(0,+∞)上的最大值是
f(-k)=.
所以 x∈(0,+∞),f(x)≤等价于f(-k)=≤.解得-≤k<0.
故当 x∈(0,+∞),f(x)≤时,k的取值范围是[-,0).
教师备选题
1.设f(x)=ln(x+1)++ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y=x在(0,0)点相切.
(1)求a,b的值;
(2)证明:当0
由y=f(x)在(0,0)点的切线斜率为,
又y′|x=0=(++a)|x=0=+a,
得a=0.
(2)证法一 由均值不等式,当x>0时,2
h′(x)=+-
=-
<-
=.
令g(x)=(x+6)3-216(x+1),则当0
因此g(x)在(0,2)内是递减函数,又由g(0)=0,得
g(x)<0,所以h′(x)<0.
因此h(x)在(0,2)内是递减函数,
又h(0)=0,得h(x)<0.于是
当0
由均值不等式,当x>0时,
2
故k(x)<0,即ln(x+1)
<[3x(x+1)+(x+6)(3+)-18(x+1)]
=(7x-18)<0.
因此h(x)在(0,2)内单调递减,又h(0)=0,
所以h(x)<0,即f(x)<.
