2.1.1 合情推理 课件1
图片预览






文档简介
课件42张PPT。第 二 章推理与证明2.1 合情推理与演绎推理
2.1.1 合情推理 自主学习 新知突破1.了解合情推理的含义,能利用归纳和类比等进行简单的推理.
2.了解合情推理在数学发现中的作用.[问题1] 我们熟知的《三国演义》第46回草船借箭中诸葛亮先生的推理过程是怎样的呢?
[提示1] 诸葛亮“先生”的推理过程是
[问题2] 蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是用肺呼吸的,蜥蜴是用肺呼吸的,蛇,鳄鱼,海龟,蜥蜴都是爬行动物,所有的爬行动物都是用肺呼吸的吗?
[提示2] 是.所有的爬行动物都是用肺呼吸的.
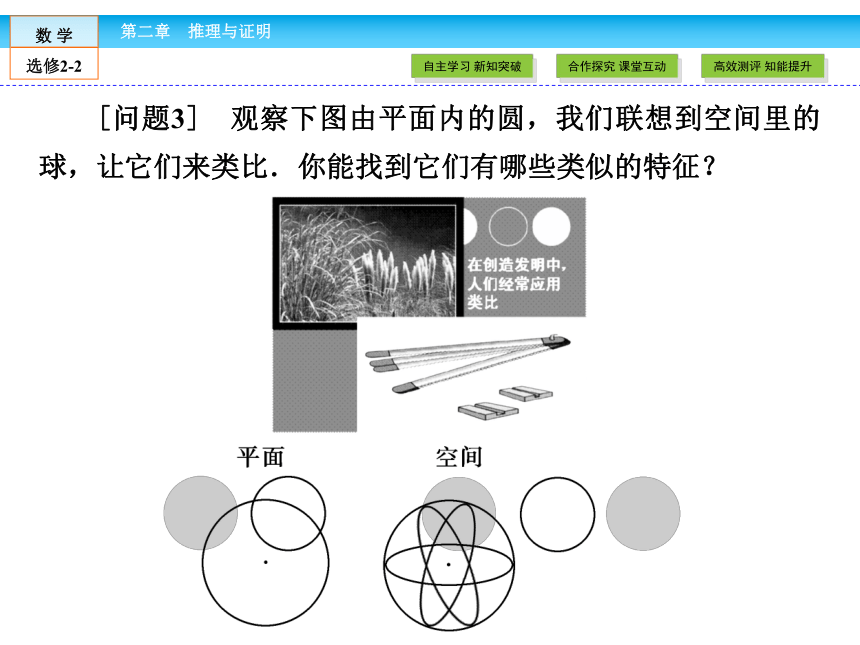
[问题3] 观察下图由平面内的圆,我们联想到空间里的球,让它们来类比.你能找到它们有哪些类似的特征?
[提示3] 鲁班类比草叶的边缘发明了锯,平面中的圆与空间中的球有类似的特征.归纳推理 部分对象全部对象个别事实一般结论部分到整体个别到一般1.归纳推理的特点与应用
(1)归纳推理是由几个已知的特殊情况归纳出一般性的结论,该结论超越了前提所包含的范围.
(2)归纳出的结论具有猜测性质,是否属实,还需逻辑证明和实践检验.即结论不一定可靠.
(3)归纳立足于观察、实验或经验的基础上,是一种具有创造性的推理,通过归纳推理得到的猜想,可以作为进一步研究的起点,帮助人们发现问题和提出问题. 类比推理 类似已知特征特殊到特殊
2.类比推理的特点及适用前提
(1)类比推理的特点
①类比是由已经解决的问题和已经获得的知识出发,推测正在研究的事物的属性,提出新问题,作出新发现.
②类比的结果是猜测性的,不一定可靠,但它有发现功能.
(2)类比推理的适用前提
①运用类比推理的前提是两类对象在某些性质上有相似性或一致性,关键是把这些相似性或一致性确切地表述出来,再由一类对象具有的特性去推断另一类对象也可能具有的特性.
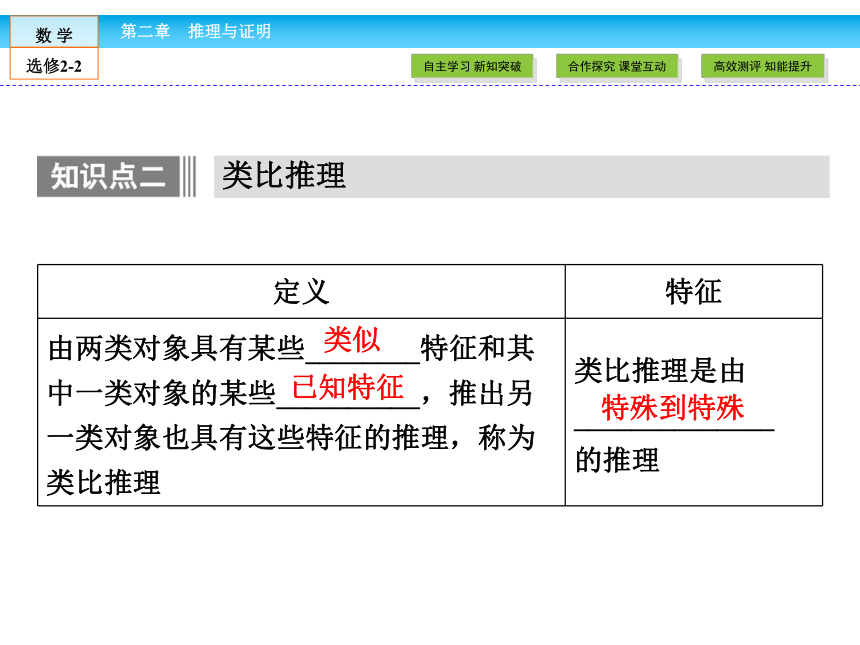
②运用类比推理常常先要寻找合适的类比对象.1.合情推理的含义
归纳推理和类比推理都是根据已有的事实,经过______、_______、______、______,再进行_______、______,然后提出_______的推理,我们把它们统称为合情推理.
2.合情推理的过程合情推理 观察分析比较联想归纳类比猜想1.下列哪个平面图形与空间的平行六面体作为类比对象比较合适的是( )
A.三角形 B.梯形
C.平行四边形 D.矩形
解析: 由类比推理的定义和特点判断,易知选C.
答案: C
2.下列关于归纳推理的说法错误的是( )
A.归纳推理是一种从一般到一般的推理过程
B.归纳推理是一种从特殊到一般的推理过程
C.归纳推理得出的结论不一定正确
D.归纳推理具有由具体到抽象的认知功能
解析: 归纳推理是由特殊到一般的推理,其结论不一定正确,但能为探寻结论(一般性)提供明确的方向,故B、C、D正确,而A错误.故选A.
答案: A4.已知数列{an}满足a1=1,an+1=2an+1(n=1,2,3…)
(1)求a2,a3,a4,a5;
(2)归纳猜想通项公式an.
解析: (1)a1=1,
a2=3=22-1,
a3=7=23-1,
a4=15=24-1,
a5=31=25-1.
(2)可归纳猜想出an=2n-1(n∈N*).合作探究 课堂互动 数列中的归纳推理 [思路点拨] 归纳推理的步骤
在数列中,常用归纳推理猜测通项公式或前n项和公式,归纳推理具有由特殊到一般,由具体到抽象的认知功能,归纳推理的一般步骤:
(1)通过观察个别情况发现某些相同性质.
(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想). 图形中的归纳推理 在一次珠宝展览会上,某商家展出了一套珠宝首饰,第一件首饰是1颗珠宝,第二件首饰是由6颗珠宝构成如图①所示的正六边形,第三件首饰是由15颗珠宝构成的如图②所示的正六边形,第四、五件首饰分别是由28颗和45颗珠宝构成的如图③和④所示的正六边形,以后每件首饰都在前一件的基础上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断第六件首饰上应有__________颗珠宝,第n件首饰上应有________颗珠宝. 方法一:5件首饰的珠宝颗数依次为1,6=2×3,15=3×5,28=4×7,45=5×9,归纳猜想第6件首饰上的珠宝数为6×11=66(颗),第n件首饰上的珠宝颗数为n(2n-1)=2n2-n(颗).
方法二:5件首饰的珠宝颗数依次为:1,1+5,1+5+9,1+5+9+13,1+5+9+13+17,则第6件首饰上的珠宝颗数为1+5+9+13+17+21=66,即每件首饰上的珠宝数是以1为首项,4为公差的等差数列的前n项和,故第n件首饰的珠宝颗数为1+5+9+…+(4n-3)=2n2-n.
答案: 66 2n2-n 图形中归纳推理的特点及思路
1.此类题目的特点:
由一组平面或空间图形,归纳猜想其数量的变化规律,这类题颇有智力趣题的味道,解答时常用归纳推理的方法解决,分析时要注意规律的寻找.
2.解决这类问题从哪入手:
(1)从图形的数量规律入手,找到数值变化与数量的关系.
(2)从图形的结构变化规律入手,找到图形的结构每发生一次变化后,与上一次比较,数值发生了怎样变化.2.在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,36, 45,55,…这些数叫做三角形数,这是因为这些数目的点可以排成正三角形(如图所示),则三角形数的一般表达式f(n)=( )答案: D类比推理 如图所示,在△ABC中,射影定理可表示为a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,类比上述定理,写出对空间四面体性质的猜想.
[思路点拨] 这是一个由平面图形到空间图形的类比,于是联想到:边长→面积,平面角→二面角,边的射影→面的射影等. 类比推理的步骤
运用类比推理必须寻找合适的类比对象,充分挖掘事物的本质及内在联系.在应用类比推理时,其一般步骤为:
(1)找出两类对象之间可以确切表述的相似性(或一致性).
(2)用一类对象的性质去推测另一类对象的性质,从而得出一个猜想.
(3)检验这个猜想.
3.在平面上,若两个正三角形的边长的比为1∶2,则它们的面积比为1∶4.类似地,在空间中,若两个正四面体的棱长的比为1∶2,它们的体积比为多少?你能验证这个结论吗?◎如图①,在三棱锥S-ABC中,平面SAB,平面SAC,平面SBC与底面ABC所成角分别为α1,α2,α3,三条侧棱SC,SB,SA与底面ABC所成的角为β1,β2,β3,三侧面△SAB,△SAC,△SBC的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间图形的一个猜想.高效测评 知能提升 完成练习册作业谢谢观看!
2.1.1 合情推理 自主学习 新知突破1.了解合情推理的含义,能利用归纳和类比等进行简单的推理.
2.了解合情推理在数学发现中的作用.[问题1] 我们熟知的《三国演义》第46回草船借箭中诸葛亮先生的推理过程是怎样的呢?
[提示1] 诸葛亮“先生”的推理过程是
[问题2] 蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是用肺呼吸的,蜥蜴是用肺呼吸的,蛇,鳄鱼,海龟,蜥蜴都是爬行动物,所有的爬行动物都是用肺呼吸的吗?
[提示2] 是.所有的爬行动物都是用肺呼吸的.
[问题3] 观察下图由平面内的圆,我们联想到空间里的球,让它们来类比.你能找到它们有哪些类似的特征?
[提示3] 鲁班类比草叶的边缘发明了锯,平面中的圆与空间中的球有类似的特征.归纳推理 部分对象全部对象个别事实一般结论部分到整体个别到一般1.归纳推理的特点与应用
(1)归纳推理是由几个已知的特殊情况归纳出一般性的结论,该结论超越了前提所包含的范围.
(2)归纳出的结论具有猜测性质,是否属实,还需逻辑证明和实践检验.即结论不一定可靠.
(3)归纳立足于观察、实验或经验的基础上,是一种具有创造性的推理,通过归纳推理得到的猜想,可以作为进一步研究的起点,帮助人们发现问题和提出问题. 类比推理 类似已知特征特殊到特殊
2.类比推理的特点及适用前提
(1)类比推理的特点
①类比是由已经解决的问题和已经获得的知识出发,推测正在研究的事物的属性,提出新问题,作出新发现.
②类比的结果是猜测性的,不一定可靠,但它有发现功能.
(2)类比推理的适用前提
①运用类比推理的前提是两类对象在某些性质上有相似性或一致性,关键是把这些相似性或一致性确切地表述出来,再由一类对象具有的特性去推断另一类对象也可能具有的特性.
②运用类比推理常常先要寻找合适的类比对象.1.合情推理的含义
归纳推理和类比推理都是根据已有的事实,经过______、_______、______、______,再进行_______、______,然后提出_______的推理,我们把它们统称为合情推理.
2.合情推理的过程合情推理 观察分析比较联想归纳类比猜想1.下列哪个平面图形与空间的平行六面体作为类比对象比较合适的是( )
A.三角形 B.梯形
C.平行四边形 D.矩形
解析: 由类比推理的定义和特点判断,易知选C.
答案: C
2.下列关于归纳推理的说法错误的是( )
A.归纳推理是一种从一般到一般的推理过程
B.归纳推理是一种从特殊到一般的推理过程
C.归纳推理得出的结论不一定正确
D.归纳推理具有由具体到抽象的认知功能
解析: 归纳推理是由特殊到一般的推理,其结论不一定正确,但能为探寻结论(一般性)提供明确的方向,故B、C、D正确,而A错误.故选A.
答案: A4.已知数列{an}满足a1=1,an+1=2an+1(n=1,2,3…)
(1)求a2,a3,a4,a5;
(2)归纳猜想通项公式an.
解析: (1)a1=1,
a2=3=22-1,
a3=7=23-1,
a4=15=24-1,
a5=31=25-1.
(2)可归纳猜想出an=2n-1(n∈N*).合作探究 课堂互动 数列中的归纳推理 [思路点拨] 归纳推理的步骤
在数列中,常用归纳推理猜测通项公式或前n项和公式,归纳推理具有由特殊到一般,由具体到抽象的认知功能,归纳推理的一般步骤:
(1)通过观察个别情况发现某些相同性质.
(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想). 图形中的归纳推理 在一次珠宝展览会上,某商家展出了一套珠宝首饰,第一件首饰是1颗珠宝,第二件首饰是由6颗珠宝构成如图①所示的正六边形,第三件首饰是由15颗珠宝构成的如图②所示的正六边形,第四、五件首饰分别是由28颗和45颗珠宝构成的如图③和④所示的正六边形,以后每件首饰都在前一件的基础上,按照这种规律增加一定数量的珠宝,使它构成更大的正六边形,依此推断第六件首饰上应有__________颗珠宝,第n件首饰上应有________颗珠宝. 方法一:5件首饰的珠宝颗数依次为1,6=2×3,15=3×5,28=4×7,45=5×9,归纳猜想第6件首饰上的珠宝数为6×11=66(颗),第n件首饰上的珠宝颗数为n(2n-1)=2n2-n(颗).
方法二:5件首饰的珠宝颗数依次为:1,1+5,1+5+9,1+5+9+13,1+5+9+13+17,则第6件首饰上的珠宝颗数为1+5+9+13+17+21=66,即每件首饰上的珠宝数是以1为首项,4为公差的等差数列的前n项和,故第n件首饰的珠宝颗数为1+5+9+…+(4n-3)=2n2-n.
答案: 66 2n2-n 图形中归纳推理的特点及思路
1.此类题目的特点:
由一组平面或空间图形,归纳猜想其数量的变化规律,这类题颇有智力趣题的味道,解答时常用归纳推理的方法解决,分析时要注意规律的寻找.
2.解决这类问题从哪入手:
(1)从图形的数量规律入手,找到数值变化与数量的关系.
(2)从图形的结构变化规律入手,找到图形的结构每发生一次变化后,与上一次比较,数值发生了怎样变化.2.在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,36, 45,55,…这些数叫做三角形数,这是因为这些数目的点可以排成正三角形(如图所示),则三角形数的一般表达式f(n)=( )答案: D类比推理 如图所示,在△ABC中,射影定理可表示为a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,类比上述定理,写出对空间四面体性质的猜想.
[思路点拨] 这是一个由平面图形到空间图形的类比,于是联想到:边长→面积,平面角→二面角,边的射影→面的射影等. 类比推理的步骤
运用类比推理必须寻找合适的类比对象,充分挖掘事物的本质及内在联系.在应用类比推理时,其一般步骤为:
(1)找出两类对象之间可以确切表述的相似性(或一致性).
(2)用一类对象的性质去推测另一类对象的性质,从而得出一个猜想.
(3)检验这个猜想.
3.在平面上,若两个正三角形的边长的比为1∶2,则它们的面积比为1∶4.类似地,在空间中,若两个正四面体的棱长的比为1∶2,它们的体积比为多少?你能验证这个结论吗?◎如图①,在三棱锥S-ABC中,平面SAB,平面SAC,平面SBC与底面ABC所成角分别为α1,α2,α3,三条侧棱SC,SB,SA与底面ABC所成的角为β1,β2,β3,三侧面△SAB,△SAC,△SBC的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间图形的一个猜想.高效测评 知能提升 完成练习册作业谢谢观看!
