2.1.1 合情推理 课件2
图片预览











文档简介
课件41张PPT。第二章 推理与证明
2.1 合情推理与演绎推理
2.1.1 合情推理 从前有个财主,想教儿子识字,请来一位教书先生.先生把着学生的笔杆儿,写一横,告诉是个“一”字;写两横,告诉是个“二”字;写三横,告诉是个“三”字.学到这里,儿子就告诉父亲说:
“我已经学会了写字,不
用先生再教了.”于是,
财主就把教书先生给辞退了. 一天,财主要邀请一位姓万的朋友,叫儿子写张请帖.财主的儿子怎么写的?1.理解归纳推理、类比推理的概念,掌握归纳
推理、类比推理的方法技巧.(重点)
2.掌握归纳法的步骤,体会归纳推理、类比推理
在数学发现中的作用.(难点)探究点1 归纳推理 【1】1742年哥德巴赫(Goldbach ,1690~1764, 是德国一位中学教师,也是一位著名的数学家, 1725年当选为俄国彼得堡科学院院士)观察到:猜想:任何一个不小于6的偶数都等于两个奇质数之和. 任何一个不小于6的偶数都等于两个奇质数之和.哥德巴赫猜想哥德巴赫猜想的过程:具体的材料观察分析猜想出一般性的结论【3】成语“一叶知秋”【2】统计初步中的用样本估计总体 通过从总体中抽取部分对象进行观测或试验, 进而对整体作出推断. 意思是从一片树叶的凋落,知道秋天将要来到.比喻由细微的迹象看出整体形势的变化,由部分推知全体. 由某类事物的 具有某些特征,推出
该类事物的 都具有这些特征的推理,或者由
概括出 的推理,称为归纳推理(简
称归纳).归纳推理特点:部分→ 整体,个别→ 一般.铜、铁、铝、金、银等金属都能导电,猜想:所有金属都导电.又如 猜想: 部分对象全部对象个别事实一般结论 分析:数列的通项公式表示的是数列{an}的第n项an与序号n之间的对应关系.为此,我们先根据已知的递推公式,算出数列的前几项.解:当n=1时,a1=1;当n=2时,当n=3时,当n=4时, 观察可得,数列的前4项都等于相应序号的倒数.
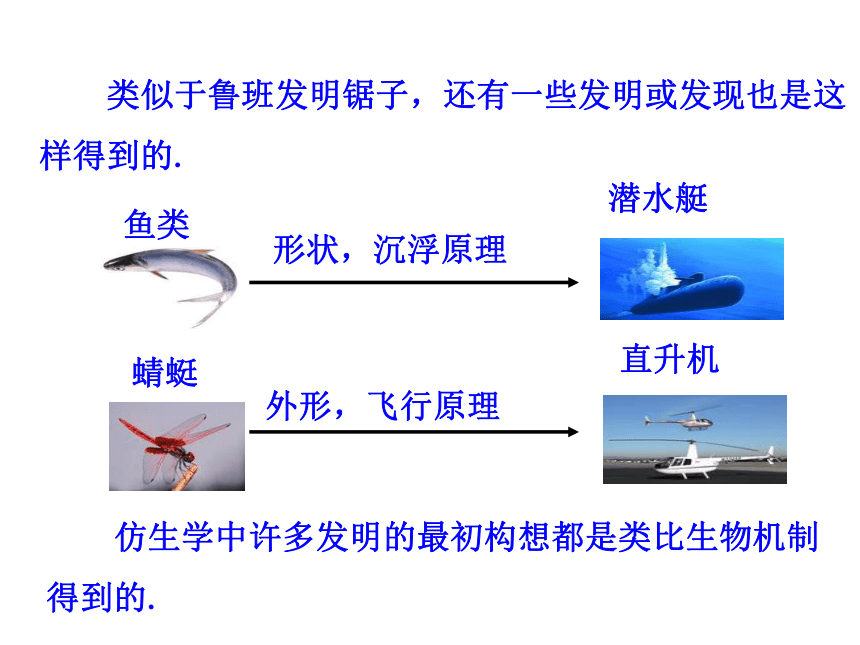
由此猜想,这个数列的通项公式为 春秋时代的鲁班在林中砍柴时被齿形草叶割破了手,他由此受到启发从而发明了锯.探究点2 类比推理 类似于鲁班发明锯子,还有一些发明或发现也是这样得到的.鱼类潜水艇蜻蜓直升机 仿生学中许多发明的最初构想都是类比生物机制得到的.可能有生命存在有生命存在温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否有生命?火星与地球类比的思维过程:火星地球存在类
似特征类比推理的过程(步骤)观察、比较联想、类推猜想新结论 由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.类比推理(1)类比推理是由特殊到特殊的推理. (2)运用类比推理常常先要寻找合适的类比对象,我们可以从不同的角度出发确定类比对象,基本原则是要根据当前问题的需要,选择适当的类比对象.(1)类比是从人们已经掌握的事物的属性,推断正在研究中的事物的属性,它以已有知识为基础,类比出新的结论.(2)是从一事物的特殊属性推断另一种事物的特殊属性.(3)类比的结果具有猜测性.类比推理的特点例2 类比实数的加法和乘法,列出它们相似的运算性质.分析:实数的加法和乘法都是由两个数参与的运算,都满足一定的运算律,都存在逆运算,而且“0”和“1”分别在加法和乘法中占有特殊的地位.因此,我们可以从上述4个方面来类比这两种运算.解:(1)两个实数经过加法运算或乘法运算后,所得的结果仍然是一个实数.(2)从运算律的角度考虑,加法和乘法都满足交换律和结合律,即(3)从逆运算的角度考虑,二者都有逆运算,加法的逆运算是减法,乘法的逆运算是除法,这就使得方程都有唯一解(4)在加法中,任意实数与0相加都不改变大小;乘法中的1与加法中的0类似,即任意实数与1的积都等于原来的数.即三角形思考:你认为平面几何中的哪一类图形可以作为四面体的类比对象?例3:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.分析:考虑到直角三角形的两条边互相垂直,我们可以选取有3个面两两垂直的四面体,作为直角三角形的类比对象.解:如上图,在Rt△ABC中,∠C=90°.设a,b,c分别表示三条边的长度,由勾股定理,得类比勾股定理的结构,我们猜想成立.【总结提升】提出猜想观察、分析、比较、联想归纳、类比从具体问题出发通俗地说,合情推理是指“合乎情理”的推理. 例4 如图所示,有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上. 1.每次只能移动1个金属片;
2.较大的金属片不能放在较小的金属片上面.
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?分析:我们从移动1,2,3,4个金属片的情形入手,探究其中的规律性,进而归纳出移动n个金属片所需的次数.解:当n=1时,只需把金属片从1号针移到3号针,用符号(13)表示,共移动了1次.
当n=2时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动顺序是: (1)把第1个金属片从1号针移到2号针;
(2)把第2个金属片从1号针移到3号针;
(3)把第1个金属片从2号针移到3号针;
用符号表示为:(12)(13)(23)
共移动了3次.
当n=3时,把上面两个金属片作为一个整体,归结为n=2的情形,移动顺序是:
(1)把上面两个金属片从1号针移到2号针; (2)把第3个金属片从1号针移到3号针;
(3)把上面两个金属片从2号针移到3号针;
其中(1)和(3)都需要借助中间针.用符号表示为:
(13)(12)(32);(13);(21)(23)(13)
共移动了7次.
当n=4时,把上面3个金属片作为一个整体,移动顺序是:
(1)把上面3个金属片从1号针移到2号针; (2)把第4个金属片从1号针移到3号针;
(3)把上面3个金属片从2号针移到3号针;
用符号表示为:
(12)(13)(23)(12)(31)(32)(12);(13);(23)(21)(31)(23)(12)(13)(23).
共移动了15次.
至此,我们得到依次移动1,2,3,4个金属片所需次数构成的数列.1,3,7,15.
观察这个数列,可以发现其中蕴含着如下规律: 由此我们猜想:若把n个金属片从1号针移到3号针,最少需要移动an次,则数列{an}的通项公式为:思考:把n个金属片从1号针移到3号针, 怎样移动才能达到最少的移动次数呢? 通过探究上述n=1,2,3,4时的移动方法,我们可以归纳出对n个金属片都适用的移动方法.当移动n个金属片时,可分为下列3个步骤:(1)把上面(n-1)个金属片从1号针移到2号针;
(2)把第n个金属片从1号针移到3号针;
(3)把上面(n-1)个金属片从2号针移到3号针.这样就把移动n个金属片的任务,转化为移动两次(n-1)个金属片和移动一次第n个金属片的任务.
而移动(n-1)个金属片需要移动两次(n-2)个金属片和移动一次第(n-1)个金属片,移动(n-2)个金属片需要移动两次(n-3)个金属片和移动一次第(n-2)个金属片……如此继续.直到转化为移动1个金属片的情形.根据这个过程,可得递推公式从这个递推公式出发,可以证明(1)式是正确的. 一般来说,由合情推理所获得的结论,仅仅是一种猜想,未必可靠.费马猜想:
同样地,类比推理所得的结论也不一定可靠,你能举一个例子吗? 半个世纪之后,欧拉发现:猜想:不是质数,从而推翻了费马的猜想BC3.甲、乙、丙三位同学被问到是否去过 A、B 、C 三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一城市;
由此可判断乙去过的城市为________.解:由丙可知,乙至少去过一个城市,由甲说可知甲去过A,C且比乙多,故乙只去过一个城市,且没有去过C城市,故乙只去过A城市.A1.归纳推理、类比推理的定义.2. 推理的一般思维过程:观察、分析概括、推广、类比提出猜想3.归纳、类比推理的特点 没有礁石,就没有美丽的浪花;没有挫折,就没有壮丽的人生.
2.1 合情推理与演绎推理
2.1.1 合情推理 从前有个财主,想教儿子识字,请来一位教书先生.先生把着学生的笔杆儿,写一横,告诉是个“一”字;写两横,告诉是个“二”字;写三横,告诉是个“三”字.学到这里,儿子就告诉父亲说:
“我已经学会了写字,不
用先生再教了.”于是,
财主就把教书先生给辞退了. 一天,财主要邀请一位姓万的朋友,叫儿子写张请帖.财主的儿子怎么写的?1.理解归纳推理、类比推理的概念,掌握归纳
推理、类比推理的方法技巧.(重点)
2.掌握归纳法的步骤,体会归纳推理、类比推理
在数学发现中的作用.(难点)探究点1 归纳推理 【1】1742年哥德巴赫(Goldbach ,1690~1764, 是德国一位中学教师,也是一位著名的数学家, 1725年当选为俄国彼得堡科学院院士)观察到:猜想:任何一个不小于6的偶数都等于两个奇质数之和. 任何一个不小于6的偶数都等于两个奇质数之和.哥德巴赫猜想哥德巴赫猜想的过程:具体的材料观察分析猜想出一般性的结论【3】成语“一叶知秋”【2】统计初步中的用样本估计总体 通过从总体中抽取部分对象进行观测或试验, 进而对整体作出推断. 意思是从一片树叶的凋落,知道秋天将要来到.比喻由细微的迹象看出整体形势的变化,由部分推知全体. 由某类事物的 具有某些特征,推出
该类事物的 都具有这些特征的推理,或者由
概括出 的推理,称为归纳推理(简
称归纳).归纳推理特点:部分→ 整体,个别→ 一般.铜、铁、铝、金、银等金属都能导电,猜想:所有金属都导电.又如 猜想: 部分对象全部对象个别事实一般结论 分析:数列的通项公式表示的是数列{an}的第n项an与序号n之间的对应关系.为此,我们先根据已知的递推公式,算出数列的前几项.解:当n=1时,a1=1;当n=2时,当n=3时,当n=4时, 观察可得,数列的前4项都等于相应序号的倒数.
由此猜想,这个数列的通项公式为 春秋时代的鲁班在林中砍柴时被齿形草叶割破了手,他由此受到启发从而发明了锯.探究点2 类比推理 类似于鲁班发明锯子,还有一些发明或发现也是这样得到的.鱼类潜水艇蜻蜓直升机 仿生学中许多发明的最初构想都是类比生物机制得到的.可能有生命存在有生命存在温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否有生命?火星与地球类比的思维过程:火星地球存在类
似特征类比推理的过程(步骤)观察、比较联想、类推猜想新结论 由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.类比推理(1)类比推理是由特殊到特殊的推理. (2)运用类比推理常常先要寻找合适的类比对象,我们可以从不同的角度出发确定类比对象,基本原则是要根据当前问题的需要,选择适当的类比对象.(1)类比是从人们已经掌握的事物的属性,推断正在研究中的事物的属性,它以已有知识为基础,类比出新的结论.(2)是从一事物的特殊属性推断另一种事物的特殊属性.(3)类比的结果具有猜测性.类比推理的特点例2 类比实数的加法和乘法,列出它们相似的运算性质.分析:实数的加法和乘法都是由两个数参与的运算,都满足一定的运算律,都存在逆运算,而且“0”和“1”分别在加法和乘法中占有特殊的地位.因此,我们可以从上述4个方面来类比这两种运算.解:(1)两个实数经过加法运算或乘法运算后,所得的结果仍然是一个实数.(2)从运算律的角度考虑,加法和乘法都满足交换律和结合律,即(3)从逆运算的角度考虑,二者都有逆运算,加法的逆运算是减法,乘法的逆运算是除法,这就使得方程都有唯一解(4)在加法中,任意实数与0相加都不改变大小;乘法中的1与加法中的0类似,即任意实数与1的积都等于原来的数.即三角形思考:你认为平面几何中的哪一类图形可以作为四面体的类比对象?例3:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.分析:考虑到直角三角形的两条边互相垂直,我们可以选取有3个面两两垂直的四面体,作为直角三角形的类比对象.解:如上图,在Rt△ABC中,∠C=90°.设a,b,c分别表示三条边的长度,由勾股定理,得类比勾股定理的结构,我们猜想成立.【总结提升】提出猜想观察、分析、比较、联想归纳、类比从具体问题出发通俗地说,合情推理是指“合乎情理”的推理. 例4 如图所示,有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上. 1.每次只能移动1个金属片;
2.较大的金属片不能放在较小的金属片上面.
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?分析:我们从移动1,2,3,4个金属片的情形入手,探究其中的规律性,进而归纳出移动n个金属片所需的次数.解:当n=1时,只需把金属片从1号针移到3号针,用符号(13)表示,共移动了1次.
当n=2时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动顺序是: (1)把第1个金属片从1号针移到2号针;
(2)把第2个金属片从1号针移到3号针;
(3)把第1个金属片从2号针移到3号针;
用符号表示为:(12)(13)(23)
共移动了3次.
当n=3时,把上面两个金属片作为一个整体,归结为n=2的情形,移动顺序是:
(1)把上面两个金属片从1号针移到2号针; (2)把第3个金属片从1号针移到3号针;
(3)把上面两个金属片从2号针移到3号针;
其中(1)和(3)都需要借助中间针.用符号表示为:
(13)(12)(32);(13);(21)(23)(13)
共移动了7次.
当n=4时,把上面3个金属片作为一个整体,移动顺序是:
(1)把上面3个金属片从1号针移到2号针; (2)把第4个金属片从1号针移到3号针;
(3)把上面3个金属片从2号针移到3号针;
用符号表示为:
(12)(13)(23)(12)(31)(32)(12);(13);(23)(21)(31)(23)(12)(13)(23).
共移动了15次.
至此,我们得到依次移动1,2,3,4个金属片所需次数构成的数列.1,3,7,15.
观察这个数列,可以发现其中蕴含着如下规律: 由此我们猜想:若把n个金属片从1号针移到3号针,最少需要移动an次,则数列{an}的通项公式为:思考:把n个金属片从1号针移到3号针, 怎样移动才能达到最少的移动次数呢? 通过探究上述n=1,2,3,4时的移动方法,我们可以归纳出对n个金属片都适用的移动方法.当移动n个金属片时,可分为下列3个步骤:(1)把上面(n-1)个金属片从1号针移到2号针;
(2)把第n个金属片从1号针移到3号针;
(3)把上面(n-1)个金属片从2号针移到3号针.这样就把移动n个金属片的任务,转化为移动两次(n-1)个金属片和移动一次第n个金属片的任务.
而移动(n-1)个金属片需要移动两次(n-2)个金属片和移动一次第(n-1)个金属片,移动(n-2)个金属片需要移动两次(n-3)个金属片和移动一次第(n-2)个金属片……如此继续.直到转化为移动1个金属片的情形.根据这个过程,可得递推公式从这个递推公式出发,可以证明(1)式是正确的. 一般来说,由合情推理所获得的结论,仅仅是一种猜想,未必可靠.费马猜想:
同样地,类比推理所得的结论也不一定可靠,你能举一个例子吗? 半个世纪之后,欧拉发现:猜想:不是质数,从而推翻了费马的猜想BC3.甲、乙、丙三位同学被问到是否去过 A、B 、C 三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一城市;
由此可判断乙去过的城市为________.解:由丙可知,乙至少去过一个城市,由甲说可知甲去过A,C且比乙多,故乙只去过一个城市,且没有去过C城市,故乙只去过A城市.A1.归纳推理、类比推理的定义.2. 推理的一般思维过程:观察、分析概括、推广、类比提出猜想3.归纳、类比推理的特点 没有礁石,就没有美丽的浪花;没有挫折,就没有壮丽的人生.
