2.3 数学归纳法 课件1
图片预览









文档简介
课件40张PPT。2.3 数学归纳法自主学习 新知突破1.了解数学归纳法的原理.
2.能用数学归纳法证明一些简单的数学命题.下图为多米诺骨牌:
如何保证骨牌一一倒下?需要几个步骤才能做到?
[提示] (1)处理第一个问题;(相当于推倒第一块骨牌)
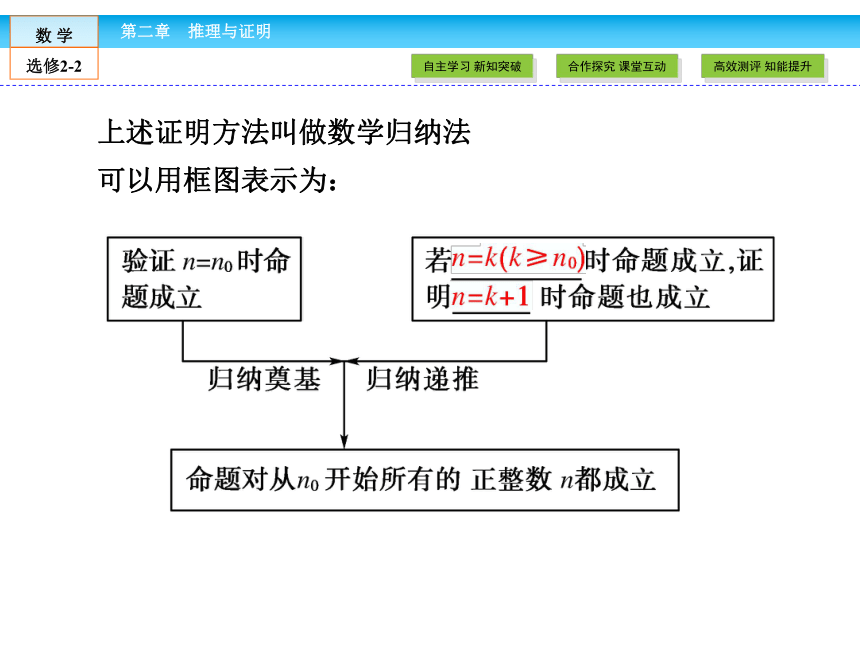
(2)验证前一问题与后一问题有递推关系.(相当于前牌推倒后牌)一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
1.(归纳奠基)证明当n取___________ (n0∈N*)时命题成立;
2.(归纳递推)假设 ___________________时命题成立,证明当__________时命题也成立.
只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立.第一个值n0n=k(k≥n0,k∈N*)n=k+1上述证明方法叫做数学归纳法
可以用框图表示为:数学归纳法的应用及注意事项
(1)数学归纳法的应用范围是证明与正整数有关的恒等式、不等式、数的整除性、几何问题,探求数列的通项及前n项和等.
(2)应用数学归纳法应注意:
①数学归纳法仅适用于与正整数n有关的数学命题的证明.
②验证是证明的基础,递推是证明的关键,二者缺一不可;
③在证明n=k+1命题成立时,必须使用归纳假设的结论,否则就不是数学归纳法.1.用数学归纳法证明“凸n边形的内角和等于(n-2)π”时,归纳奠基中n0的取值应为( )
A.1 B.2
C.3 D.4
解析: 边数最少的凸n边形为三角形,故n0=3.
答案: C答案: D
3.用数学归纳法证明关于n的恒等式时,当n=k时,表达式为1×4+2×7+…+k(3k+1)=k(k+1)2,则当n=k+1时,表达式为__________ .
解析: 当n=k+1时,应将表达式1×4+2×7+…+k(3k+1)=k(k+1)2中的k更换为k+1.
答案: 1×4+2×7…+k(3k+1)+(k+1)(3k+4)=(k+1)(k+2)24.用数学归纳法证明:1+5+9+…+(4n-3)=(2n-1)·n.
证明: ①当n=1时,左边=1,右边=1,命题成立.
②假设n=k(k≥1,k∈N*)时,命题成立,
即1+5+9+…+(4k-3)=k(2k-1).
则当n=k+1时,左边=1+5+9+…+(4k-3)+(4k+1)
=k(2k-1)+(4k+1)=2k2+3k+1=(2k+1)(k+1)
=[2(k+1)-1](k+1)=右边,
∴当n=k+1时,命题成立.
由①②知,对一切n∈N*,命题成立.合作探究 课堂互动 用数学归纳法证明等式或不等式 [思路点拨] 用数学归纳法证明与正整数有关的等式命题时,关键在于“先看项”,弄清等式两边的构成规律,等式的两边各有多少项,项的多少与n的取值是否有关,由n=k到n=k+1时,等式两边会增加多少项. 用数学归纳法证明几何问题 用数学归纳法证明几何问题的关键是“找项”,即几何元素从k个变成(k+1)个时,所证的几何量将增加多少,这需用到几何知识或借助于几何图形来分析.在实在分析不出来的情况下,将n=k+1和n=k分别代入所证的式子,然后作差,即可求出增加量,然后只需稍加说明即可,这也是用数学归纳法证明几何命题的一大技巧. 归纳—猜想—证明 “观察—归纳—猜想—证明”模式的题目的解法
(1)观察:由已知条件写出前几项;
(2)归纳:找出前几项的规律,找到项与项数的关系;
(3)猜想:猜想出通项公式;
(4)证明:用数学归纳法证明猜想的形式,因为猜想不一定正确,所以要通过数学归纳法给出证明. 3.数列{an}的前n项和为Sn,满足2Sn=a+n,an>0(n∈N*),
(1)求a1,a2,a3的值,并猜想数列{an}的通项公式;
(2)用数学归纳法证明(1)中的猜想.
解析: (1)由2Sn=a+n得
当n=1时,2a1=a+1,∴a1=1.
当n=2时,2S2=a+2,∴a2=2.
当n=3时,2S3=a+3,∴a3=3.
猜想:数列{an}的通项公式为an=n.【错因】 没有利用归纳假设进行证明.第(2)步,不可以直接利用等比数列的求和公式求出当n=k+1时式子的和,在证明n=k+1时,一定要利用“归纳假设”.高效测评 知能提升 完成练习册作业谢谢观看!
2.能用数学归纳法证明一些简单的数学命题.下图为多米诺骨牌:
如何保证骨牌一一倒下?需要几个步骤才能做到?
[提示] (1)处理第一个问题;(相当于推倒第一块骨牌)
(2)验证前一问题与后一问题有递推关系.(相当于前牌推倒后牌)一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
1.(归纳奠基)证明当n取___________ (n0∈N*)时命题成立;
2.(归纳递推)假设 ___________________时命题成立,证明当__________时命题也成立.
只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立.第一个值n0n=k(k≥n0,k∈N*)n=k+1上述证明方法叫做数学归纳法
可以用框图表示为:数学归纳法的应用及注意事项
(1)数学归纳法的应用范围是证明与正整数有关的恒等式、不等式、数的整除性、几何问题,探求数列的通项及前n项和等.
(2)应用数学归纳法应注意:
①数学归纳法仅适用于与正整数n有关的数学命题的证明.
②验证是证明的基础,递推是证明的关键,二者缺一不可;
③在证明n=k+1命题成立时,必须使用归纳假设的结论,否则就不是数学归纳法.1.用数学归纳法证明“凸n边形的内角和等于(n-2)π”时,归纳奠基中n0的取值应为( )
A.1 B.2
C.3 D.4
解析: 边数最少的凸n边形为三角形,故n0=3.
答案: C答案: D
3.用数学归纳法证明关于n的恒等式时,当n=k时,表达式为1×4+2×7+…+k(3k+1)=k(k+1)2,则当n=k+1时,表达式为__________ .
解析: 当n=k+1时,应将表达式1×4+2×7+…+k(3k+1)=k(k+1)2中的k更换为k+1.
答案: 1×4+2×7…+k(3k+1)+(k+1)(3k+4)=(k+1)(k+2)24.用数学归纳法证明:1+5+9+…+(4n-3)=(2n-1)·n.
证明: ①当n=1时,左边=1,右边=1,命题成立.
②假设n=k(k≥1,k∈N*)时,命题成立,
即1+5+9+…+(4k-3)=k(2k-1).
则当n=k+1时,左边=1+5+9+…+(4k-3)+(4k+1)
=k(2k-1)+(4k+1)=2k2+3k+1=(2k+1)(k+1)
=[2(k+1)-1](k+1)=右边,
∴当n=k+1时,命题成立.
由①②知,对一切n∈N*,命题成立.合作探究 课堂互动 用数学归纳法证明等式或不等式 [思路点拨] 用数学归纳法证明与正整数有关的等式命题时,关键在于“先看项”,弄清等式两边的构成规律,等式的两边各有多少项,项的多少与n的取值是否有关,由n=k到n=k+1时,等式两边会增加多少项. 用数学归纳法证明几何问题 用数学归纳法证明几何问题的关键是“找项”,即几何元素从k个变成(k+1)个时,所证的几何量将增加多少,这需用到几何知识或借助于几何图形来分析.在实在分析不出来的情况下,将n=k+1和n=k分别代入所证的式子,然后作差,即可求出增加量,然后只需稍加说明即可,这也是用数学归纳法证明几何命题的一大技巧. 归纳—猜想—证明 “观察—归纳—猜想—证明”模式的题目的解法
(1)观察:由已知条件写出前几项;
(2)归纳:找出前几项的规律,找到项与项数的关系;
(3)猜想:猜想出通项公式;
(4)证明:用数学归纳法证明猜想的形式,因为猜想不一定正确,所以要通过数学归纳法给出证明. 3.数列{an}的前n项和为Sn,满足2Sn=a+n,an>0(n∈N*),
(1)求a1,a2,a3的值,并猜想数列{an}的通项公式;
(2)用数学归纳法证明(1)中的猜想.
解析: (1)由2Sn=a+n得
当n=1时,2a1=a+1,∴a1=1.
当n=2时,2S2=a+2,∴a2=2.
当n=3时,2S3=a+3,∴a3=3.
猜想:数列{an}的通项公式为an=n.【错因】 没有利用归纳假设进行证明.第(2)步,不可以直接利用等比数列的求和公式求出当n=k+1时式子的和,在证明n=k+1时,一定要利用“归纳假设”.高效测评 知能提升 完成练习册作业谢谢观看!
