3.1.1 数系的扩充和复数的概念 课件1
文档属性
| 名称 | 3.1.1 数系的扩充和复数的概念 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 1023.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-16 21:27:59 | ||
图片预览











文档简介
课件38张PPT。第 三 章数系的扩充与复数的引入3.1 数系的扩充和复数的概念
3.1.1 数系的扩充和复数的概念自主学习 新知突破1.了解数系的扩充过程.
2.理解复数的基本概念以及复数相等的充要条件.
3.了解复数的代数表示法.[问题1] 方程2x2-3x+1=0.试求方程的整数解?方程的实数解?
[问题2] 方程x2+1=0在实数范围内有解吗?
[提示2] 没有解.
[问题3] 若有一个新数i满足i2=-1,试想方程x2+1=0有解吗?
[提示3] 有解,x=i但不是实数范围内.
[问题4] 实数a与实数b和i相乘的结果相加,结果记作a+bi,这一新数集形式如何表示?
[提示4] C={a+bi|a,b∈R}.1.复数的定义:形如__________的数叫做复数.其中i叫做__________,满足:i2=_______.
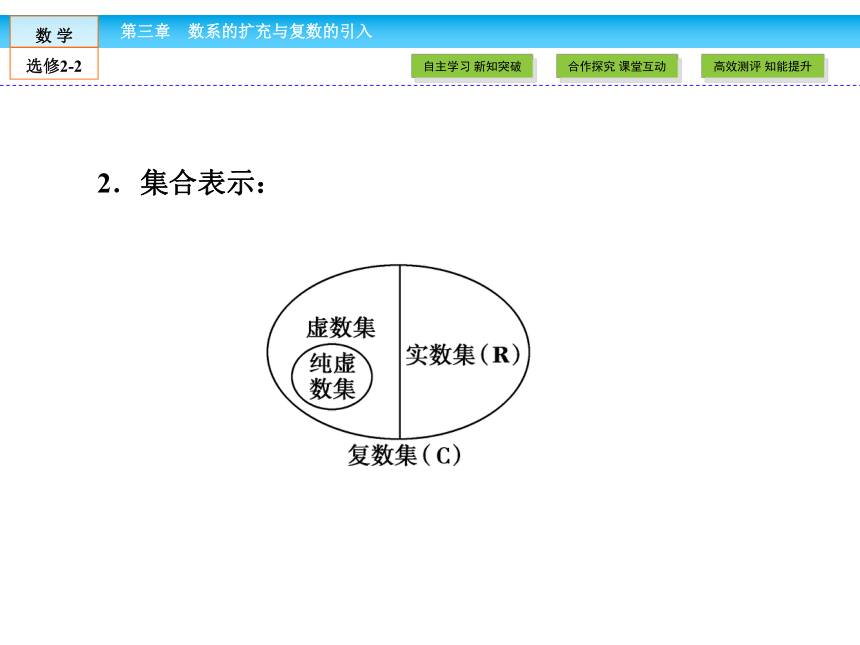
2.复数的表示:复数通常用字母z表示,即__________,这种表示形式叫做复数的代数形式,其中实数a叫做复数z的________,实数b叫做复数z的________.复数的概念及其代数表示法 a+bi虚数单位-1z=a+bi实部虚部1.复数的分类:复数的分类 2.集合表示:设a,b,c,d都是实数,那么a+bi=c+di?___________.复数相等的充要条件 a=c且b=d1.理解复数与复数集的概念时应注意以下几点
(1)复数集是最大的数集,任何一个数都可写成a+bi(a,b∈R)的形式,其中0=0+0i.
(2)复数的虚部是实数b而非bi.
(3)复数z=a+bi只有在a,b∈R时才是复数的代数形式,否则不是代数形式.
2.复数代数形式的应用
(1)从代数形式可判定z是实数、虚数还是纯虚数.
若z是纯虚数,可设z=bi(b≠0,b∈R)
若z是虚数,可设z=a+bi(b≠0,b∈R)
若z是复数,可设z=a+bi(a,b∈R)
(2)当两个复数不全是实数时,不能比较大小,只可判定相等或不相等,但两个复数都是实数时,可以比较大小.1.复数i-i2的虚部为( )
A.0 B.1
C.i D.-2
解析: i-i2=1+i.
答案: B
2.用C,R和I分别表示复数集、实数集和虚数集,那么有( )
A.C=R∩I B.R∩I={0}
C.R=C∩I D.R∩I=?
解析: 由复数的概念可知R?C,I?C,R∩I=?.
答案: D
3.如果(m2-1)+(m2-2m)i>0,则实数m的值为________.
答案: 2
4.如果(x+y)+(x+3)i=(3x+2y)+yi,求实数x,y的值.合作探究 课堂互动 复数的概念及分类 下列命题中,正确命题的个数是( )
①复数-3i+5的实部是-3,虚部是5;
②若x,y∈C,则x+yi=1+i的充要条件是x=y=1;
③若x2+y2=0,则x=y=0.
A.0 B.1
C.2 D.3
[思路点拨] 本题主要考查复数的基本概念及分类,解题时要注意a+bi中,a,b的取值为实数.
解析: ①-3i+5=5-3i,∴-3i+5的实部是5,虚部是-3,①是假命题.②由于x,y∈C,所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,②是假命题.③当x=1,y=i时,x2+y2=0成立,∴③是假命题.
故选A.
答案: A
在理解概念时,一定要抓住概念的本质,抓住新概念与以前知识的不同之处,尤其是应该满足的条件.利用举反例的形式否定一个命题是很有效的方法.
1.设复数z=a+bi(a,b∈R),则z为纯虚数的必要不充分条件是( )
A.a=0 B.a=0且b≠0
C.a≠0且b=0 D.a≠0且b≠0
解析: 由纯虚数的概念可知:a=0且b≠0是复数z=a+bi(a,b∈R)为纯虚数的充要条件.而题中要选择的是必要不充分条件.因此,我们要选择的应该是由“且”字连接的复合命题“a=0且b≠0”的子命题,“a=0”或“b≠0”.对照各选择项的情况,故选A.
答案: A复数的概念 [思路点拨]
复数的分类:
复数z=a+bi(a,b∈R),当满足①b=0时复数z是实数,②b≠0时复数z是虚数,③a=0,b≠0时复数z是纯虚数.研究一个复数在什么情况下是实数、虚数或纯虚数时,首先要保证这个复数的实部、虚部是否有意义.
特别提醒:特别注意复数是实数、虚数和纯虚数时,采用的是标准形式的代数式,若不是复数的标准代数形式,应先化为复数的标准代数形式z=a+bi(a,b∈R),再依据概念求解、判断复数是实数,仅注重虚部为零是不够的,还需要考虑它的实部是否有意义.复数相等的充要条件[思路点拨] 确定实部与虚部,列方程组求解. 1.一般地,两个复数只能相等或不相等,不能比较大小.
2.复数相等的充要条件是求复数及解方程的主要依据,是复数问题实数化的桥梁纽带.
3.必须在标准代数形式下确定实部、虚部后才可应用. 3.(1)若4-3a-a2i=a2+4ai,则实数a=________.
(2)已知x2-y2+2xyi=2i,求实数x,y的值.
答案: (1)-4◎求满足条件-2+a-(b-a)i>-5+(a+2b-6)i的实数a,b的取值情况.【错因】 错解想当然地认为大的复数所对应的实部和虚部都大,而忽视了只有实数才能比较大小的前提,因此本题中的复数应为实数.高效测评 知能提升 完成练习册作业谢谢观看!
3.1.1 数系的扩充和复数的概念自主学习 新知突破1.了解数系的扩充过程.
2.理解复数的基本概念以及复数相等的充要条件.
3.了解复数的代数表示法.[问题1] 方程2x2-3x+1=0.试求方程的整数解?方程的实数解?
[问题2] 方程x2+1=0在实数范围内有解吗?
[提示2] 没有解.
[问题3] 若有一个新数i满足i2=-1,试想方程x2+1=0有解吗?
[提示3] 有解,x=i但不是实数范围内.
[问题4] 实数a与实数b和i相乘的结果相加,结果记作a+bi,这一新数集形式如何表示?
[提示4] C={a+bi|a,b∈R}.1.复数的定义:形如__________的数叫做复数.其中i叫做__________,满足:i2=_______.
2.复数的表示:复数通常用字母z表示,即__________,这种表示形式叫做复数的代数形式,其中实数a叫做复数z的________,实数b叫做复数z的________.复数的概念及其代数表示法 a+bi虚数单位-1z=a+bi实部虚部1.复数的分类:复数的分类 2.集合表示:设a,b,c,d都是实数,那么a+bi=c+di?___________.复数相等的充要条件 a=c且b=d1.理解复数与复数集的概念时应注意以下几点
(1)复数集是最大的数集,任何一个数都可写成a+bi(a,b∈R)的形式,其中0=0+0i.
(2)复数的虚部是实数b而非bi.
(3)复数z=a+bi只有在a,b∈R时才是复数的代数形式,否则不是代数形式.
2.复数代数形式的应用
(1)从代数形式可判定z是实数、虚数还是纯虚数.
若z是纯虚数,可设z=bi(b≠0,b∈R)
若z是虚数,可设z=a+bi(b≠0,b∈R)
若z是复数,可设z=a+bi(a,b∈R)
(2)当两个复数不全是实数时,不能比较大小,只可判定相等或不相等,但两个复数都是实数时,可以比较大小.1.复数i-i2的虚部为( )
A.0 B.1
C.i D.-2
解析: i-i2=1+i.
答案: B
2.用C,R和I分别表示复数集、实数集和虚数集,那么有( )
A.C=R∩I B.R∩I={0}
C.R=C∩I D.R∩I=?
解析: 由复数的概念可知R?C,I?C,R∩I=?.
答案: D
3.如果(m2-1)+(m2-2m)i>0,则实数m的值为________.
答案: 2
4.如果(x+y)+(x+3)i=(3x+2y)+yi,求实数x,y的值.合作探究 课堂互动 复数的概念及分类 下列命题中,正确命题的个数是( )
①复数-3i+5的实部是-3,虚部是5;
②若x,y∈C,则x+yi=1+i的充要条件是x=y=1;
③若x2+y2=0,则x=y=0.
A.0 B.1
C.2 D.3
[思路点拨] 本题主要考查复数的基本概念及分类,解题时要注意a+bi中,a,b的取值为实数.
解析: ①-3i+5=5-3i,∴-3i+5的实部是5,虚部是-3,①是假命题.②由于x,y∈C,所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,②是假命题.③当x=1,y=i时,x2+y2=0成立,∴③是假命题.
故选A.
答案: A
在理解概念时,一定要抓住概念的本质,抓住新概念与以前知识的不同之处,尤其是应该满足的条件.利用举反例的形式否定一个命题是很有效的方法.
1.设复数z=a+bi(a,b∈R),则z为纯虚数的必要不充分条件是( )
A.a=0 B.a=0且b≠0
C.a≠0且b=0 D.a≠0且b≠0
解析: 由纯虚数的概念可知:a=0且b≠0是复数z=a+bi(a,b∈R)为纯虚数的充要条件.而题中要选择的是必要不充分条件.因此,我们要选择的应该是由“且”字连接的复合命题“a=0且b≠0”的子命题,“a=0”或“b≠0”.对照各选择项的情况,故选A.
答案: A复数的概念 [思路点拨]
复数的分类:
复数z=a+bi(a,b∈R),当满足①b=0时复数z是实数,②b≠0时复数z是虚数,③a=0,b≠0时复数z是纯虚数.研究一个复数在什么情况下是实数、虚数或纯虚数时,首先要保证这个复数的实部、虚部是否有意义.
特别提醒:特别注意复数是实数、虚数和纯虚数时,采用的是标准形式的代数式,若不是复数的标准代数形式,应先化为复数的标准代数形式z=a+bi(a,b∈R),再依据概念求解、判断复数是实数,仅注重虚部为零是不够的,还需要考虑它的实部是否有意义.复数相等的充要条件[思路点拨] 确定实部与虚部,列方程组求解. 1.一般地,两个复数只能相等或不相等,不能比较大小.
2.复数相等的充要条件是求复数及解方程的主要依据,是复数问题实数化的桥梁纽带.
3.必须在标准代数形式下确定实部、虚部后才可应用. 3.(1)若4-3a-a2i=a2+4ai,则实数a=________.
(2)已知x2-y2+2xyi=2i,求实数x,y的值.
答案: (1)-4◎求满足条件-2+a-(b-a)i>-5+(a+2b-6)i的实数a,b的取值情况.【错因】 错解想当然地认为大的复数所对应的实部和虚部都大,而忽视了只有实数才能比较大小的前提,因此本题中的复数应为实数.高效测评 知能提升 完成练习册作业谢谢观看!
