上海市崇明县2015-2016学年八年级(上)期末数学试卷(解析版)
文档属性
| 名称 | 上海市崇明县2015-2016学年八年级(上)期末数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 195.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-16 19:35:13 | ||
图片预览



文档简介
2015-2016学年上海市崇明县八年级(上)期末数学试卷
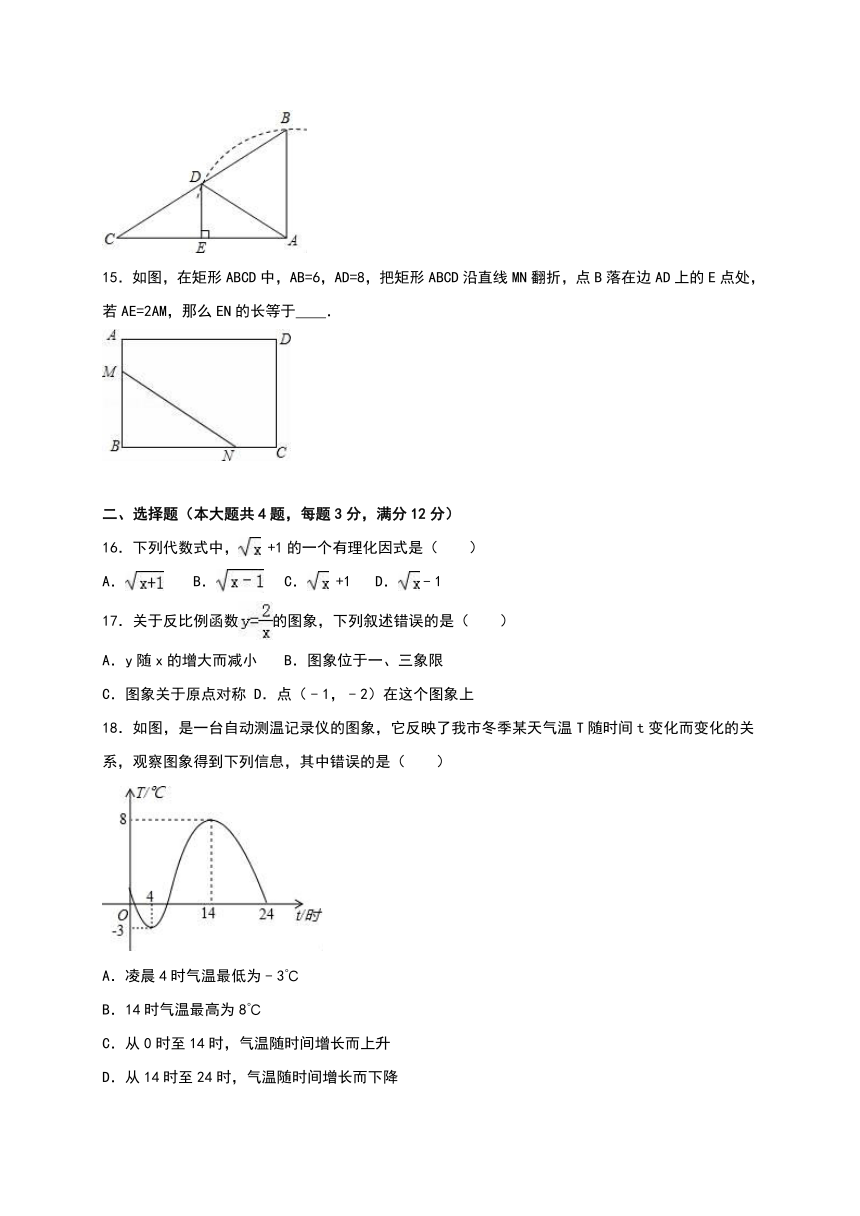
一、填空题(本大题共15题,每题2分,满分30分)
1.化简:
= .
2.方程x2=4x的根为 .
3.函数的定义域是 .
4.如果最简二次根式与是同类二次根式,那么x的值是 .
5.已知f(x)=,则= .
6.在实数范围内分解因式:x2﹣3x﹣2= .
7.已知关于x的方程x2﹣2x+3k=0没有实数根,则k的取值范围是 .
8.已知P(x1,y1),Q(x2,y2)在反比例函数的图象上,若x1<x2<0,则y1 y2
(填“>”“<”或“=”).
9.如果反比例函数的图象经过点(﹣2,1),那么这个反比例函数的解析式是 .
10.命题“对顶角相等”的逆命题是 .
11.到点P(﹣5,0)的距离等于4的点的轨迹是 .
12.如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于 .
13.如图,在△ABC中,∠ABC=56°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠ABE= 度.
14.如图,在Rt△ABC中,∠BAC=
( http: / / www.21cnjy.com )90°,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
15.如图,在矩形ABCD中,AB=6,A
( http: / / www.21cnjy.com )D=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于 .
二、选择题(本大题共4题,每题3分,满分12分)
16.下列代数式中,
+1的一个有理化因式是( )
A.
B.
C.
+1
D.﹣1
17.关于反比例函数的图象,下列叙述错误的是( )
A.y随x的增大而减小
B.图象位于一、三象限
C.图象关于原点对称
D.点(﹣1,﹣2)在这个图象上
18.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低为﹣3℃
B.14时气温最高为8℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
19.如图,在平面直角坐标系中,直线AB与
( http: / / www.21cnjy.com )x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=(k≠0)上,则k的值为( )
A.4
B.﹣2
C.
D.﹣
三、简答题(本大题共4题,每题6分,满分24分)
20.计算:.
21.解方程:(2x+1)(x﹣1)=8(9﹣x)﹣1.
22.已知关于x的一元二次方程ax2﹣(4a+1)x+(4a﹣1)=0有两个实数根.
(1)求a的取值范围;
(2)当a在允许的取值范围内取最小的整数时,请用配方法解此方程.
23.如图,在△ABC中,
( http: / / www.21cnjy.com )AB=AC,作AD⊥AB交BC的延长线于点D,作AE∥BD,CE⊥AC,且AE,CE相交于点E,求证:AD=CE.
四、解答题(本大题共3题,每题8分,满分34分)
24.某药品研究所开发一种抗菌新药,经
( http: / / www.21cnjy.com )多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
25.
2013年,东营市某楼盘以
( http: / / www.21cnjy.com )每平方米6500元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调
( http: / / www.21cnjy.com )相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
26.如图,已知在△ABC中,∠BAC=90
( http: / / www.21cnjy.com )°,AB=AC,点D在边BC上,作∠DAF=90°,且AF=AD,过点F作EF∥AD,且EF=AF,联结CF,CE.
(1)求证:FC⊥BC;
(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.
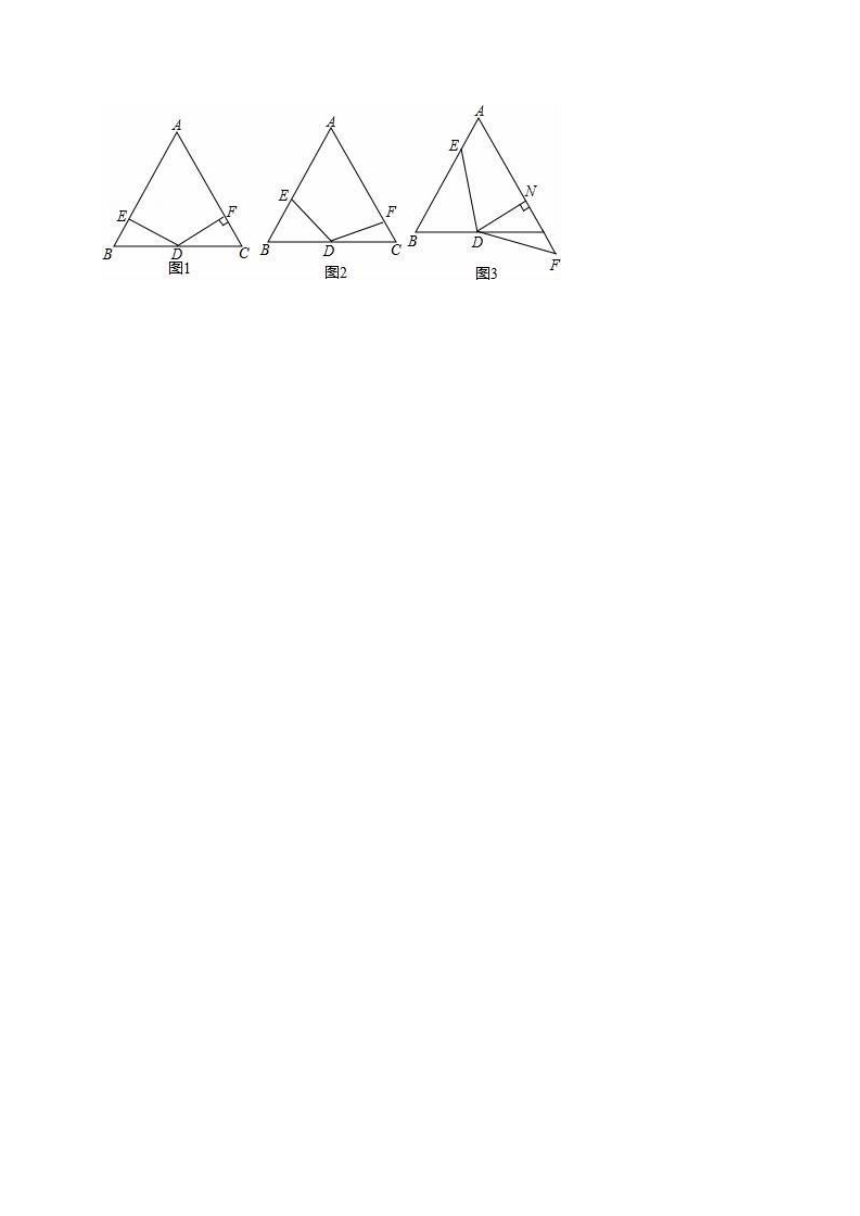
27.在△ABC中,AB=
( http: / / www.21cnjy.com )AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB;
(3)如图3,将(2)中
( http: / / www.21cnjy.com )的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,(2)中的结论还成立吗?若AB=4,求此时BE的长.
2015-2016学年上海市崇明县八年级(上)期末数学试卷
参考答案与试题解析
一、填空题(本大题共15题,每题2分,满分30分)
1.化简:
= .
【考点】算术平方根.
【分析】根据二次根式的性质:
=×(a≥0,b≥0)解答.
【解答】解:
==2,
故答案为:2.
【点评】此题主要考查了算术平方根的定义,解答此题的关键是熟练掌握二次根式的性质,并能正确运用.
2.方程x2=4x的根为 x1=0,x2=4 .
【考点】解一元二次方程-因式分解法.
【分析】移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.
【解答】解:x2=4x,
x2﹣4x=0,
x(x﹣4)=0,
x=0,x﹣4=0,
x1=0,x2=4,
故答案为:x1=0,x2=4.
【点评】本题考查了解一元二次方程的应用,关键是能把一元二次方程转化成一元一次方程.
3.函数的定义域是 x≠﹣2 .
【考点】函数自变量的取值范围.
【分析】根据分式有意义的条件是分母不为0;分析原函数可得关系式x+2≠0,解可得答案.
【解答】解:根据题意可得x+2≠0;
解得x≠﹣2;
故答案为x≠﹣2.
【点评】本题考查了函数自变量的取值范围,当函数表达式是分式时,要注意考虑分式的分母不能为0.
4.如果最简二次根式与是同类二次根式,那么x的值是 1 .
【考点】同类二次根式;最简二次根式.
【分析】根据题意,它们的被开方数相同,列出方程求解.
【解答】解:由最简二次根式与是同类二次根式,得
x+2=3x.
解得x=1,
故答案为1.
【点评】本题考查同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.
5.已知f(x)=,则= +1 .
【考点】函数值.
【分析】将x=代入f(x)=,再化简即可得.
【解答】解:当x=时,
===+1,
故答案为:
+1.
【点评】本题考查求函数值的能力,当已知函数解析式时,求函数值就是求代数式的值.
6.在实数范围内分解因式:x2﹣3x﹣2= .
【考点】实数范围内分解因式.
【分析】首先令x2﹣3x﹣2=0,利用公式法即可求得此一元二次方程的解,继而可将此多项式分解.
【解答】解:令x2﹣3x﹣2=0,
则a=1,b=﹣3,c=﹣2,
∴x==,
∴x2﹣3x﹣2=.
故答案为:.
【点评】本题考查实数范围内的因式分解.注意掌握公式法解一元二次方程的知识.
7.已知关于x的方程x2﹣2x+3k=0没有实数根,则k的取值范围是 k> .
【考点】根的判别式.
【分析】由方程没有实数根结合根的判别式,可得出关于k的一元一次不等式,解不等式即可得出结论.
【解答】解:∵关于x的方程x2﹣2x+3k=0没有实数根,
∴△=(﹣2)2﹣4×1×3k=4﹣12k<0,
解得:k>.
故答案为:k>.
【点评】本题考查了根的判别式以及解一元
( http: / / www.21cnjy.com )一次不等式,解题的关键是得出△=4﹣12k<0.本题属于基础题,难度不大,解决该题型题目时,根据方程根的情况结合根的判别式,得出不等式(或不等式组)是关键.
8.已知P(x1,y1),Q(x2,y2)在反比例函数的图象上,若x1<x2<0,则y1 > y2
(填“>”“<”或“=”).
【考点】反比例函数图象上点的坐标特征.
【分析】根据反比例函数的比例系数k>0可知,该函数在x<0内单调递减,再结合x1<x2<0,即可得出结论.
【解答】解:∵反比例函数中k>0,
∴该函数在x<0内单调递减.
∵x1<x2<0,
∴y1>y2.
故答案为:>.
【点评】本题考查了反比例函数的性质,解
( http: / / www.21cnjy.com )题的关键是得出反比例函数在x<0内单调递减.本题属于基础题,难度不大,解决该题型题目时,根据系数k的取值范围确定函数的单调性是关键.
9.如果反比例函数的图象经过点(﹣2,1),那么这个反比例函数的解析式是 y=﹣ .
【考点】待定系数法求反比例函数解析式.
【分析】设y=,直接把点(﹣2,1)代入求解.
【解答】解:设y=.
把(﹣2,1)代入,得
k=xy=﹣2,
则y=﹣,
故答案为y=﹣.
【点评】此题考查了运用待定系数法求反比例函数解析式的方法.
10.命题“对顶角相等”的逆命题是 相等的角为对顶角 .
【考点】命题与定理.
【分析】交换原命题的题设与结论即可得到其逆命题.
【解答】解:命题“对顶角相等”的逆命题是“相等的角为对顶角”.
故答案为相等的角为对顶角.
【点评】本题考查了命题与定理:判断
( http: / / www.21cnjy.com )一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.
有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了逆命题.
11.到点P(﹣5,0)的距离等于4的点的轨迹是 以P为圆心4为半径的圆 .
【考点】轨迹.
【分析】只需根据圆的定义即可解决问题.
【解答】解:如图所示,到点P(﹣5,0)的距离等于4的点的轨迹是以P为圆心4为半径的圆.
故答案为以P为圆心4为半径的圆.
【点评】本题主要考查的是圆的定义,其中圆是到定点的距离等于定长的点的集合,属于中考常考题型.
12.如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于 8 .
【考点】勾股定理;直角三角形斜边上的中线.
【专题】计算题.
【分析】由“直角三角形斜边上的中线等于斜边的一半”求得AC=2DE=10;然后在直角△ACD中,利用勾股定理来求线段CD的长度即可.
【解答】解:如图,∵△ABC中,CD⊥AB于D,E是AC的中点,DE=5,
∴DE=AC=5,
∴AC=10.
在直角△ACD中,∠ADC=90°,AD=6,AC=10,则根据勾股定理,得
CD===8.
故答案是:8.
【点评】本题考查了勾股定理,直角三角形斜边上的中线.利用直角三角形斜边上的中线等于斜边的一半求得AC的长度是解题的难点.
13.如图,在△ABC中,∠ABC=56°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠ABE= 28 度.
【考点】三角形的外角性质;角平分线的性质.
【分析】过点E作EG⊥AD于G,作EH⊥
( http: / / www.21cnjy.com )BF于H,作EK⊥AC于K,根据角平分线上的点到脚的两边距离相等可得EG=EK,EH=EK,从而得到EG=EH,再根据到角的两边距离相等的点在角的平分线上可得BE平分∠ABC,然后求解即可.
【解答】解:如图,过点E作EG⊥AD于G,作EH⊥BF于H,作EK⊥AC于K,
∵∠DAC和∠ACF的平分线交于点E,
∴EG=EK,EH=EK,
∴EG=EH,
∴BE平分∠ABC,
∴∠ABE=∠ABC=×56°=28°.
故答案为:28.
【点评】本题考查了角平分线上的点到脚
( http: / / www.21cnjy.com )的两边距离相等的性质,到角的两边距离相等的点在角的平分线上的性质,熟记性质并作出辅助线判断出BE是角平分线是解题的关键.
14.如图,在Rt△ABC中,∠BAC
( http: / / www.21cnjy.com )=90°,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
【考点】含30度角的直角三角形.
【分析】先根据∠C=30°,∠
( http: / / www.21cnjy.com )BAC=90°,DE⊥AC可知BC=2AB,CD=2DE,再由AB=AD可知点D是斜边BC的中点,由此可用a表示出AB的长,根据勾股定理可得出AC的长,由此可得出结论.
【解答】解:∵∠C=30°,∠BAC=90°,DE⊥AC,
∴BC=2AB,CD=2DE=2a.
∵AB=AD,
∴点D是斜边BC的中点,
∴BC=2CD=4a,AB=BC=2a,
∴AC===2a,
∴△ABC的周长=AB+BC+AC=2a+4a+2a=(6+2)a.
故答案为:(6+2)a.
【点评】本题考查的是含30°的直角三角形,熟知在直角三角形中,30°角所对的直角边等于斜边的一半是解答此题的关键.
15.如图,在矩形ABCD中,AB=6
( http: / / www.21cnjy.com ),AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于 3 .
【考点】矩形的性质;翻折变换(折叠问题).
【分析】设AM=x,表示出EM=BM=6﹣
( http: / / www.21cnjy.com )x,AE=2x,再利用勾股定理列出方程求出x,然后求出BM,AE,过点N作NF⊥AD于F,求出△AME和△FEN,再利用相似三角形对应边成比例列式求解即可.
【解答】解:设AM=x,则EM=BM=6﹣x,AE=2AM=2x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴在Rt△AME中,由勾股定理得,AM2+AE2=EM2,
即x2+(2x)2=(6﹣x)2,
整理得,x2+3x﹣9=0,
解得x1=,x2=(舍去),
所以,BM=6﹣=,AE=﹣3+3,
过点N作NF⊥AD于F,易求△AME∽△FEN,
所以,,
即,
解得EN=3.
故答案为:3.
【点评】本题考查了翻折变换的
( http: / / www.21cnjy.com )性质,勾股定理,相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键,难点在于利用勾股定理列方程求出AM的长度.
二、选择题(本大题共4题,每题3分,满分12分)
16.下列代数式中,
+1的一个有理化因式是( )
A.
B.
C.
+1
D.﹣1
【考点】分母有理化.
【分析】根据有理化因式的定义进行求解即可.两个含有根式的代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.
【解答】解:∵由平方差公式,()()=x﹣1,
∴的有理化因式是,
故选D.
【点评】本题主要考查了对有理化因式的理解,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.
17.关于反比例函数的图象,下列叙述错误的是( )
A.y随x的增大而减小
B.图象位于一、三象限
C.图象关于原点对称
D.点(﹣1,﹣2)在这个图象上
【考点】反比例函数的性质.
【分析】根据反比例函数的性质用排除法解答.
【解答】解:A:反比例函数解析式中k=2>0,则在同一个象限内,y随x增大而减小,选项中没有提到每个象限,故错误;
B:2>0,图象经过一三象限,故正确;
C:反比例函数图象都是关于原点对称的,故正确;
D:把x=﹣1代入函数解析式,求得y=﹣2,故正确.
故选:A.
【点评】本题考查了反比例函数的性质,解题的关键是要明确反比例函数的增减性必须要强调在同一个象限内.
18.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低为﹣3℃
B.14时气温最高为8℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
【考点】函数的图象.
【分析】根据函数的图象对各选项进行逐一分析即可.
【解答】解:A、∵由图象可知,在凌晨4点函数图象在最低点﹣3,∴凌晨4时气温最低为﹣3℃,故本选项正确;
B、∵由图象可知,在14点函数图象在最高点8,∴14时气温最高为8℃,故本选项正确;
C、∵由图象可知,从4时至14时,气温随时间增长而上升,不是从0点,故本选项错误;
D、∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确.
故选C.
【点评】本题考查的是函数的图象,能根据函数图象在坐标系中的增减性判断出函数的增减性是解答此题的关键.
19.如图,在平面直角坐标系中,直线A
( http: / / www.21cnjy.com )B与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=(k≠0)上,则k的值为( )
A.4
B.﹣2
C.
D.﹣
【考点】翻折变换(折叠问题);待定系数法求反比例函数解析式.
【分析】设点C的坐标为(x,y),过点
( http: / / www.21cnjy.com )C作CD⊥x轴,作CE⊥y轴,由折叠的性质易得∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,用锐角三角函数的定义得CD,CE,得点C的坐标,易得k.
【解答】解:设点C的坐标为(x,y),过点C作CD⊥x轴,作CE⊥y轴,
∵将△ABO沿直线AB翻折,
∴∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,
∴CD=y=AC sin60°=2×=,
∵∠ACB=∠DCE=90°,
∴∠BCE=∠ACD=30°,
∵BC=BO=AO tan30°=2×=,
CE=|x|=BC cos30°==1,
∵点C在第二象限,
∴x=﹣1,
∵点C恰好落在双曲线y=(k≠0)上,
∴k=x y=﹣1×=﹣,
故选D.
【点评】本题主要考查了翻折的性质,锐角三角函数,反比例函数的解析式,理解翻折的性质,求点C的坐标是解答此题的关键.
三、简答题(本大题共4题,每题6分,满分24分)
20.计算:.
【考点】二次根式的混合运算.
【专题】计算题.
【分析】先分母有理化和进行二次根式的除法运算,然后化简后合并即可.
【解答】解:原式=2++3﹣+﹣
=2++3﹣+2﹣2
=4+.
【点评】本题考查了二次根式的计算:先把各
( http: / / www.21cnjy.com )二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.
21.解方程:(2x+1)(x﹣1)=8(9﹣x)﹣1.
【考点】解一元二次方程-因式分解法.
【分析】首先移项合并同类项,然后利用十字相乘法分解因式,再解两个一元一次方程即可.
【解答】解:∵2x2﹣2x+x﹣1=72﹣8x﹣1,
∴2x2+7x﹣72=0,
∴(x+8)(2x﹣9)=0,
∴x1=﹣8,x2=.
【点评】此题考查了解一元二次方程﹣因式分解法,熟练掌握因式分解的方法是解本题的关键.
22.已知关于x的一元二次方程ax2﹣(4a+1)x+(4a﹣1)=0有两个实数根.
(1)求a的取值范围;
(2)当a在允许的取值范围内取最小的整数时,请用配方法解此方程.
【考点】根的判别式;解一元二次方程-配方法.
【分析】(1)由方程有两个实数根以及该方程为一元二次方程,结合根的判别式即可得出关于a的不等式组,解不等式组即可得出a的取值范围;
(2)根据(1)的结论找出a的值,将其代入原方程中,再利用配方法解该方程即可.
【解答】解:(1)∵关于x的一元二次方程ax2﹣(4a+1)x+(4a﹣1)=0有两个实数根;
∴,即,
解得:a≥﹣且a≠0.
∴a的取值范围为a≥﹣且a≠0.
(2)∵a≥﹣且a≠0,
∴a的最小的整数为a=1,
∴原方程为x2﹣5x+3=0,即=,
∴x﹣=±,
∴x1=,x2=.
【点评】本题考查了根的判别式以及配方法解一元
( http: / / www.21cnjy.com )二次方程,解题的关键是:(1)找出关于a的不等式组;(2)确定a的值.本题属于基础题,难度不大,解决该题型题目时,根据方程根的情况结合根的判别式以及一元二次方程的定义,得出不等式组是关键.
23.如图,在△ABC中,AB=AC
( http: / / www.21cnjy.com ),作AD⊥AB交BC的延长线于点D,作AE∥BD,CE⊥AC,且AE,CE相交于点E,求证:AD=CE.
【考点】全等三角形的判定与性质.
【专题】证明题.
【分析】欲证明AD=CE,只要证明△ABD≌△CAE即可.
【解答】证明:∵AB=AC
∴∠ABC=∠ACB,
∵AE∥BD,
∴∠EAC=∠ACB,
∴∠ABC=∠EAC,
∵AD⊥AB,CE⊥AC,
∴∠BAD=∠ACE=90°,
在△ABD和△ACE中
,
∴△ABD≌△CAE,
∴AD=CE.
【点评】本题考查全等三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键,属于中考常考题型.
四、解答题(本大题共3题,每题8分,满分34分)
24.某药品研究所开发一种抗菌新药,经
( http: / / www.21cnjy.com )多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
【考点】反比例函数的应用;一次函数的应用.
【分析】(1)分别利用正比例函数以及反比例函数解析式求法得出即可;
(2)利用y=4分别得出x的值,进而得出答案.
【解答】解:(1)当0≤x≤4时,设直线解析式为:y=kx,
将(4,8)代入得:8=4k,
解得:k=2,
故直线解析式为:y=2x,
当4≤x≤10时,设反比例函数解析式为:y=,
将(4,8)代入得:8=,
解得:a=32,
故反比例函数解析式为:y=;
因此血液中药物浓度上升阶段的函数关系式为y=2x(0≤x≤4),
下降阶段的函数关系式为y=(4≤x≤10).
(2)当y=4,则4=2x,解得:x=2,
当y=4,则4=,解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间6小时.
【点评】此题主要考查了反比例函数的应用,根据题意得出函数解析式是解题关键.
25.2013年,东营市某楼盘以每平方米
( http: / / www.21cnjy.com )6500元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调
( http: / / www.21cnjy.com )相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
【考点】一元二次方程的应用.
【专题】增长率问题.
【分析】(1)设平均每年下调的百分率为x,根据题意列出方程,求出方程的解即可得到结果;
(2)如果下调的百分率相同,求出2016年的房价,进而确定出100平方米的总房款,即可做出判断.
【解答】解:(1)设平均每年下调的百分率为x,
根据题意得:6500(1﹣x)2=5265,
解得:x1=0.1=10%,x2=1.9(舍去),
则平均每年下调的百分率为10%;
(2)如果下调的百分率相同,2016年的房价为5265×(1﹣10%)=4738.5(元/米2),
则100平方米的住房总房款为100×4738.5=473850=47.385(万元),
∵20+30>47.385,
∴张强的愿望可以实现.
【点评】此题考查了一元二次方程的应用,找出题中的等量关系是解本题的关键.
26.如图,已知在△ABC中,∠BA
( http: / / www.21cnjy.com )C=90°,AB=AC,点D在边BC上,作∠DAF=90°,且AF=AD,过点F作EF∥AD,且EF=AF,联结CF,CE.
(1)求证:FC⊥BC;
(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.
【考点】全等三角形的判定与性质;线段垂直平分线的性质;等腰直角三角形.
【分析】(1)根据正方形的性质得出AD
( http: / / www.21cnjy.com )=AF,∠FAD=90°=∠BAC,求出∠FAC=∠BAD,证出△ABD≌△ACF,推出∠B=∠FCA即可;
(2)根据△ABD≌△ACF,推出BD=CF=AC,求出∠DAC=∠EFC,根据SAS推出△DAC≌△EFC,即可得出CD=CE.
【解答】解:(1)∵∠BAC=∠DAF=90°,
∴∠BAC﹣∠DAC=∠DAF﹣∠DAC,
即∠BAD=∠CAF,
又∵AB=AC,AD=AF,
∴△ABD≌△ACF,
∴∠B=∠ACF,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠ACF=∠B=45°,
∴∠BCF=90°,
∴FC⊥BC;
(2)∵△ABD≌△ACF,
∴BD=FC,
又∵BD=AC,
∴AC=FC,
∴∠CAF=∠CFA,
∵∠DAF=90°,EF∥AD,
∴∠DAF=∠AFE=90°,
∴∠DAC=∠EFC,
∵AD=AF,EF=AF,
∴AD=FE,
∴△ADC≌△FEC,
∴CD=CE,
∴点C在线段DE的垂直平分线上.
【点评】本题考查了正方形性质,全等三角形的性质和判定,等腰直角三角形性质的应用,主要考查学生综合运用定理进行推理的能力.
27.在△ABC中,AB=A
( http: / / www.21cnjy.com )C,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB;
(3)如图3,将(2)中的
( http: / / www.21cnjy.com )∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,(2)中的结论还成立吗?若AB=4,求此时BE的长.
【考点】旋转的性质;等边三角形的判定与性质.
【分析】(1)如图1,易求得∠B=60°,∠BED=90°,BD=2,然后运用三角函数的定义就可求出BE的值;
(2)过点D作DM⊥AB于M,作DN⊥AC
( http: / / www.21cnjy.com )于N,如图2,易证△MBD≌△NCD,则有BM=CN,DM=DN,进而可证到△EMD≌△FND,则有EM=FN,就可得到BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=BC=AB;
(3)过点D作DM⊥AB于M,如图3.同(1
( http: / / www.21cnjy.com ))可得:∠B=∠ACD=60°,同(2)可得:BM=CN,DM=DN,EM=FN.由DN=FN可得DM=DN=FN=EM,从而可得BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM=2BD×sin60°=BC=AB,因为BE+CF=BE+NF﹣CN=BE+DM﹣BM=BE+BD﹣BD=AB,把AB=4,BD=2代入即可得到BE+﹣1=2,从而求得BE=+1.
【解答】解:(1)如图1,
∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∴∠B=∠C=60°,BC=AC=AB=4.
∵点D是线段BC的中点,
∴BD=DC=BC=2.
∵DF⊥AC,即∠AFD=90°,
∴∠AED=360°﹣60°﹣90°﹣120°=90°,
∴∠BED=90°,
∴BE=BD×cos∠B=2×cos60°=2×=1;
(2)过点D作DM⊥AB于M,作DN⊥AC于N,如图2,
则有∠AMD=∠BMD=∠AND=∠CND=90°.
∵∠A=60°,∴∠MDN=360°﹣60°﹣90°﹣90°=120°.
∵∠EDF=120°,∴∠MDE=∠NDF.
在△MBD和△NCD中,
,
∴△MBD≌△NCD,
∴BM=CN,DM=DN.
在△EMD和△FND中,
,
∴△EMD≌△FND,
∴EM=FN,
∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN
=2BM=2BD×cos60°=BD=BC=AB;
(3)过点D作DM⊥AB于M,如图3.
同(1)可得:∠B=∠ACD=60°.
同(2)可得:BM=CN,DM=DN,EM=FN.
∵DN=FN,
∴DM=DN=FN=EM,
∴BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM=2BD×sin60°=BC=AB,
∴(2)中的结论不成立;
∵AB=4,
∴BD=2,
∵BE+CF=BE+NF﹣CN=BE+DM﹣BM=BE+BD﹣BD=AB,
∴BE+﹣1=2,
∴BE=+1.
【点评】本题主要考查了等边三角形的判定与性质
( http: / / www.21cnjy.com )、四边形的内角和定理、全等三角形的判定与性质、三角函数的定义、特殊角的三角函数值等知识,通过证明三角形全等得到BM=CN,DM=DN,EM=FN是解决本题的关键.
一、填空题(本大题共15题,每题2分,满分30分)
1.化简:
= .
2.方程x2=4x的根为 .
3.函数的定义域是 .
4.如果最简二次根式与是同类二次根式,那么x的值是 .
5.已知f(x)=,则= .
6.在实数范围内分解因式:x2﹣3x﹣2= .
7.已知关于x的方程x2﹣2x+3k=0没有实数根,则k的取值范围是 .
8.已知P(x1,y1),Q(x2,y2)在反比例函数的图象上,若x1<x2<0,则y1 y2
(填“>”“<”或“=”).
9.如果反比例函数的图象经过点(﹣2,1),那么这个反比例函数的解析式是 .
10.命题“对顶角相等”的逆命题是 .
11.到点P(﹣5,0)的距离等于4的点的轨迹是 .
12.如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于 .
13.如图,在△ABC中,∠ABC=56°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠ABE= 度.
14.如图,在Rt△ABC中,∠BAC=
( http: / / www.21cnjy.com )90°,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
15.如图,在矩形ABCD中,AB=6,A
( http: / / www.21cnjy.com )D=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于 .
二、选择题(本大题共4题,每题3分,满分12分)
16.下列代数式中,
+1的一个有理化因式是( )
A.
B.
C.
+1
D.﹣1
17.关于反比例函数的图象,下列叙述错误的是( )
A.y随x的增大而减小
B.图象位于一、三象限
C.图象关于原点对称
D.点(﹣1,﹣2)在这个图象上
18.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低为﹣3℃
B.14时气温最高为8℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
19.如图,在平面直角坐标系中,直线AB与
( http: / / www.21cnjy.com )x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=(k≠0)上,则k的值为( )
A.4
B.﹣2
C.
D.﹣
三、简答题(本大题共4题,每题6分,满分24分)
20.计算:.
21.解方程:(2x+1)(x﹣1)=8(9﹣x)﹣1.
22.已知关于x的一元二次方程ax2﹣(4a+1)x+(4a﹣1)=0有两个实数根.
(1)求a的取值范围;
(2)当a在允许的取值范围内取最小的整数时,请用配方法解此方程.
23.如图,在△ABC中,
( http: / / www.21cnjy.com )AB=AC,作AD⊥AB交BC的延长线于点D,作AE∥BD,CE⊥AC,且AE,CE相交于点E,求证:AD=CE.
四、解答题(本大题共3题,每题8分,满分34分)
24.某药品研究所开发一种抗菌新药,经
( http: / / www.21cnjy.com )多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
25.
2013年,东营市某楼盘以
( http: / / www.21cnjy.com )每平方米6500元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调
( http: / / www.21cnjy.com )相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
26.如图,已知在△ABC中,∠BAC=90
( http: / / www.21cnjy.com )°,AB=AC,点D在边BC上,作∠DAF=90°,且AF=AD,过点F作EF∥AD,且EF=AF,联结CF,CE.
(1)求证:FC⊥BC;
(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.
27.在△ABC中,AB=
( http: / / www.21cnjy.com )AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB;
(3)如图3,将(2)中
( http: / / www.21cnjy.com )的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,(2)中的结论还成立吗?若AB=4,求此时BE的长.
2015-2016学年上海市崇明县八年级(上)期末数学试卷
参考答案与试题解析
一、填空题(本大题共15题,每题2分,满分30分)
1.化简:
= .
【考点】算术平方根.
【分析】根据二次根式的性质:
=×(a≥0,b≥0)解答.
【解答】解:
==2,
故答案为:2.
【点评】此题主要考查了算术平方根的定义,解答此题的关键是熟练掌握二次根式的性质,并能正确运用.
2.方程x2=4x的根为 x1=0,x2=4 .
【考点】解一元二次方程-因式分解法.
【分析】移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.
【解答】解:x2=4x,
x2﹣4x=0,
x(x﹣4)=0,
x=0,x﹣4=0,
x1=0,x2=4,
故答案为:x1=0,x2=4.
【点评】本题考查了解一元二次方程的应用,关键是能把一元二次方程转化成一元一次方程.
3.函数的定义域是 x≠﹣2 .
【考点】函数自变量的取值范围.
【分析】根据分式有意义的条件是分母不为0;分析原函数可得关系式x+2≠0,解可得答案.
【解答】解:根据题意可得x+2≠0;
解得x≠﹣2;
故答案为x≠﹣2.
【点评】本题考查了函数自变量的取值范围,当函数表达式是分式时,要注意考虑分式的分母不能为0.
4.如果最简二次根式与是同类二次根式,那么x的值是 1 .
【考点】同类二次根式;最简二次根式.
【分析】根据题意,它们的被开方数相同,列出方程求解.
【解答】解:由最简二次根式与是同类二次根式,得
x+2=3x.
解得x=1,
故答案为1.
【点评】本题考查同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.
5.已知f(x)=,则= +1 .
【考点】函数值.
【分析】将x=代入f(x)=,再化简即可得.
【解答】解:当x=时,
===+1,
故答案为:
+1.
【点评】本题考查求函数值的能力,当已知函数解析式时,求函数值就是求代数式的值.
6.在实数范围内分解因式:x2﹣3x﹣2= .
【考点】实数范围内分解因式.
【分析】首先令x2﹣3x﹣2=0,利用公式法即可求得此一元二次方程的解,继而可将此多项式分解.
【解答】解:令x2﹣3x﹣2=0,
则a=1,b=﹣3,c=﹣2,
∴x==,
∴x2﹣3x﹣2=.
故答案为:.
【点评】本题考查实数范围内的因式分解.注意掌握公式法解一元二次方程的知识.
7.已知关于x的方程x2﹣2x+3k=0没有实数根,则k的取值范围是 k> .
【考点】根的判别式.
【分析】由方程没有实数根结合根的判别式,可得出关于k的一元一次不等式,解不等式即可得出结论.
【解答】解:∵关于x的方程x2﹣2x+3k=0没有实数根,
∴△=(﹣2)2﹣4×1×3k=4﹣12k<0,
解得:k>.
故答案为:k>.
【点评】本题考查了根的判别式以及解一元
( http: / / www.21cnjy.com )一次不等式,解题的关键是得出△=4﹣12k<0.本题属于基础题,难度不大,解决该题型题目时,根据方程根的情况结合根的判别式,得出不等式(或不等式组)是关键.
8.已知P(x1,y1),Q(x2,y2)在反比例函数的图象上,若x1<x2<0,则y1 > y2
(填“>”“<”或“=”).
【考点】反比例函数图象上点的坐标特征.
【分析】根据反比例函数的比例系数k>0可知,该函数在x<0内单调递减,再结合x1<x2<0,即可得出结论.
【解答】解:∵反比例函数中k>0,
∴该函数在x<0内单调递减.
∵x1<x2<0,
∴y1>y2.
故答案为:>.
【点评】本题考查了反比例函数的性质,解
( http: / / www.21cnjy.com )题的关键是得出反比例函数在x<0内单调递减.本题属于基础题,难度不大,解决该题型题目时,根据系数k的取值范围确定函数的单调性是关键.
9.如果反比例函数的图象经过点(﹣2,1),那么这个反比例函数的解析式是 y=﹣ .
【考点】待定系数法求反比例函数解析式.
【分析】设y=,直接把点(﹣2,1)代入求解.
【解答】解:设y=.
把(﹣2,1)代入,得
k=xy=﹣2,
则y=﹣,
故答案为y=﹣.
【点评】此题考查了运用待定系数法求反比例函数解析式的方法.
10.命题“对顶角相等”的逆命题是 相等的角为对顶角 .
【考点】命题与定理.
【分析】交换原命题的题设与结论即可得到其逆命题.
【解答】解:命题“对顶角相等”的逆命题是“相等的角为对顶角”.
故答案为相等的角为对顶角.
【点评】本题考查了命题与定理:判断
( http: / / www.21cnjy.com )一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.
有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了逆命题.
11.到点P(﹣5,0)的距离等于4的点的轨迹是 以P为圆心4为半径的圆 .
【考点】轨迹.
【分析】只需根据圆的定义即可解决问题.
【解答】解:如图所示,到点P(﹣5,0)的距离等于4的点的轨迹是以P为圆心4为半径的圆.
故答案为以P为圆心4为半径的圆.
【点评】本题主要考查的是圆的定义,其中圆是到定点的距离等于定长的点的集合,属于中考常考题型.
12.如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于 8 .
【考点】勾股定理;直角三角形斜边上的中线.
【专题】计算题.
【分析】由“直角三角形斜边上的中线等于斜边的一半”求得AC=2DE=10;然后在直角△ACD中,利用勾股定理来求线段CD的长度即可.
【解答】解:如图,∵△ABC中,CD⊥AB于D,E是AC的中点,DE=5,
∴DE=AC=5,
∴AC=10.
在直角△ACD中,∠ADC=90°,AD=6,AC=10,则根据勾股定理,得
CD===8.
故答案是:8.
【点评】本题考查了勾股定理,直角三角形斜边上的中线.利用直角三角形斜边上的中线等于斜边的一半求得AC的长度是解题的难点.
13.如图,在△ABC中,∠ABC=56°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠ABE= 28 度.
【考点】三角形的外角性质;角平分线的性质.
【分析】过点E作EG⊥AD于G,作EH⊥
( http: / / www.21cnjy.com )BF于H,作EK⊥AC于K,根据角平分线上的点到脚的两边距离相等可得EG=EK,EH=EK,从而得到EG=EH,再根据到角的两边距离相等的点在角的平分线上可得BE平分∠ABC,然后求解即可.
【解答】解:如图,过点E作EG⊥AD于G,作EH⊥BF于H,作EK⊥AC于K,
∵∠DAC和∠ACF的平分线交于点E,
∴EG=EK,EH=EK,
∴EG=EH,
∴BE平分∠ABC,
∴∠ABE=∠ABC=×56°=28°.
故答案为:28.
【点评】本题考查了角平分线上的点到脚
( http: / / www.21cnjy.com )的两边距离相等的性质,到角的两边距离相等的点在角的平分线上的性质,熟记性质并作出辅助线判断出BE是角平分线是解题的关键.
14.如图,在Rt△ABC中,∠BAC
( http: / / www.21cnjy.com )=90°,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为 .
【考点】含30度角的直角三角形.
【分析】先根据∠C=30°,∠
( http: / / www.21cnjy.com )BAC=90°,DE⊥AC可知BC=2AB,CD=2DE,再由AB=AD可知点D是斜边BC的中点,由此可用a表示出AB的长,根据勾股定理可得出AC的长,由此可得出结论.
【解答】解:∵∠C=30°,∠BAC=90°,DE⊥AC,
∴BC=2AB,CD=2DE=2a.
∵AB=AD,
∴点D是斜边BC的中点,
∴BC=2CD=4a,AB=BC=2a,
∴AC===2a,
∴△ABC的周长=AB+BC+AC=2a+4a+2a=(6+2)a.
故答案为:(6+2)a.
【点评】本题考查的是含30°的直角三角形,熟知在直角三角形中,30°角所对的直角边等于斜边的一半是解答此题的关键.
15.如图,在矩形ABCD中,AB=6
( http: / / www.21cnjy.com ),AD=8,把矩形ABCD沿直线MN翻折,点B落在边AD上的E点处,若AE=2AM,那么EN的长等于 3 .
【考点】矩形的性质;翻折变换(折叠问题).
【分析】设AM=x,表示出EM=BM=6﹣
( http: / / www.21cnjy.com )x,AE=2x,再利用勾股定理列出方程求出x,然后求出BM,AE,过点N作NF⊥AD于F,求出△AME和△FEN,再利用相似三角形对应边成比例列式求解即可.
【解答】解:设AM=x,则EM=BM=6﹣x,AE=2AM=2x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴在Rt△AME中,由勾股定理得,AM2+AE2=EM2,
即x2+(2x)2=(6﹣x)2,
整理得,x2+3x﹣9=0,
解得x1=,x2=(舍去),
所以,BM=6﹣=,AE=﹣3+3,
过点N作NF⊥AD于F,易求△AME∽△FEN,
所以,,
即,
解得EN=3.
故答案为:3.
【点评】本题考查了翻折变换的
( http: / / www.21cnjy.com )性质,勾股定理,相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键,难点在于利用勾股定理列方程求出AM的长度.
二、选择题(本大题共4题,每题3分,满分12分)
16.下列代数式中,
+1的一个有理化因式是( )
A.
B.
C.
+1
D.﹣1
【考点】分母有理化.
【分析】根据有理化因式的定义进行求解即可.两个含有根式的代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.
【解答】解:∵由平方差公式,()()=x﹣1,
∴的有理化因式是,
故选D.
【点评】本题主要考查了对有理化因式的理解,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.
17.关于反比例函数的图象,下列叙述错误的是( )
A.y随x的增大而减小
B.图象位于一、三象限
C.图象关于原点对称
D.点(﹣1,﹣2)在这个图象上
【考点】反比例函数的性质.
【分析】根据反比例函数的性质用排除法解答.
【解答】解:A:反比例函数解析式中k=2>0,则在同一个象限内,y随x增大而减小,选项中没有提到每个象限,故错误;
B:2>0,图象经过一三象限,故正确;
C:反比例函数图象都是关于原点对称的,故正确;
D:把x=﹣1代入函数解析式,求得y=﹣2,故正确.
故选:A.
【点评】本题考查了反比例函数的性质,解题的关键是要明确反比例函数的增减性必须要强调在同一个象限内.
18.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低为﹣3℃
B.14时气温最高为8℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
【考点】函数的图象.
【分析】根据函数的图象对各选项进行逐一分析即可.
【解答】解:A、∵由图象可知,在凌晨4点函数图象在最低点﹣3,∴凌晨4时气温最低为﹣3℃,故本选项正确;
B、∵由图象可知,在14点函数图象在最高点8,∴14时气温最高为8℃,故本选项正确;
C、∵由图象可知,从4时至14时,气温随时间增长而上升,不是从0点,故本选项错误;
D、∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确.
故选C.
【点评】本题考查的是函数的图象,能根据函数图象在坐标系中的增减性判断出函数的增减性是解答此题的关键.
19.如图,在平面直角坐标系中,直线A
( http: / / www.21cnjy.com )B与x轴交于点A(﹣2,0),与x轴夹角为30°,将△ABO沿直线AB翻折,点O的对应点C恰好落在双曲线y=(k≠0)上,则k的值为( )
A.4
B.﹣2
C.
D.﹣
【考点】翻折变换(折叠问题);待定系数法求反比例函数解析式.
【分析】设点C的坐标为(x,y),过点
( http: / / www.21cnjy.com )C作CD⊥x轴,作CE⊥y轴,由折叠的性质易得∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,用锐角三角函数的定义得CD,CE,得点C的坐标,易得k.
【解答】解:设点C的坐标为(x,y),过点C作CD⊥x轴,作CE⊥y轴,
∵将△ABO沿直线AB翻折,
∴∠CAB=∠OAB=30°,AC=AO=2,∠ACB=AOB=90°,
∴CD=y=AC sin60°=2×=,
∵∠ACB=∠DCE=90°,
∴∠BCE=∠ACD=30°,
∵BC=BO=AO tan30°=2×=,
CE=|x|=BC cos30°==1,
∵点C在第二象限,
∴x=﹣1,
∵点C恰好落在双曲线y=(k≠0)上,
∴k=x y=﹣1×=﹣,
故选D.
【点评】本题主要考查了翻折的性质,锐角三角函数,反比例函数的解析式,理解翻折的性质,求点C的坐标是解答此题的关键.
三、简答题(本大题共4题,每题6分,满分24分)
20.计算:.
【考点】二次根式的混合运算.
【专题】计算题.
【分析】先分母有理化和进行二次根式的除法运算,然后化简后合并即可.
【解答】解:原式=2++3﹣+﹣
=2++3﹣+2﹣2
=4+.
【点评】本题考查了二次根式的计算:先把各
( http: / / www.21cnjy.com )二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.
21.解方程:(2x+1)(x﹣1)=8(9﹣x)﹣1.
【考点】解一元二次方程-因式分解法.
【分析】首先移项合并同类项,然后利用十字相乘法分解因式,再解两个一元一次方程即可.
【解答】解:∵2x2﹣2x+x﹣1=72﹣8x﹣1,
∴2x2+7x﹣72=0,
∴(x+8)(2x﹣9)=0,
∴x1=﹣8,x2=.
【点评】此题考查了解一元二次方程﹣因式分解法,熟练掌握因式分解的方法是解本题的关键.
22.已知关于x的一元二次方程ax2﹣(4a+1)x+(4a﹣1)=0有两个实数根.
(1)求a的取值范围;
(2)当a在允许的取值范围内取最小的整数时,请用配方法解此方程.
【考点】根的判别式;解一元二次方程-配方法.
【分析】(1)由方程有两个实数根以及该方程为一元二次方程,结合根的判别式即可得出关于a的不等式组,解不等式组即可得出a的取值范围;
(2)根据(1)的结论找出a的值,将其代入原方程中,再利用配方法解该方程即可.
【解答】解:(1)∵关于x的一元二次方程ax2﹣(4a+1)x+(4a﹣1)=0有两个实数根;
∴,即,
解得:a≥﹣且a≠0.
∴a的取值范围为a≥﹣且a≠0.
(2)∵a≥﹣且a≠0,
∴a的最小的整数为a=1,
∴原方程为x2﹣5x+3=0,即=,
∴x﹣=±,
∴x1=,x2=.
【点评】本题考查了根的判别式以及配方法解一元
( http: / / www.21cnjy.com )二次方程,解题的关键是:(1)找出关于a的不等式组;(2)确定a的值.本题属于基础题,难度不大,解决该题型题目时,根据方程根的情况结合根的判别式以及一元二次方程的定义,得出不等式组是关键.
23.如图,在△ABC中,AB=AC
( http: / / www.21cnjy.com ),作AD⊥AB交BC的延长线于点D,作AE∥BD,CE⊥AC,且AE,CE相交于点E,求证:AD=CE.
【考点】全等三角形的判定与性质.
【专题】证明题.
【分析】欲证明AD=CE,只要证明△ABD≌△CAE即可.
【解答】证明:∵AB=AC
∴∠ABC=∠ACB,
∵AE∥BD,
∴∠EAC=∠ACB,
∴∠ABC=∠EAC,
∵AD⊥AB,CE⊥AC,
∴∠BAD=∠ACE=90°,
在△ABD和△ACE中
,
∴△ABD≌△CAE,
∴AD=CE.
【点评】本题考查全等三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键,属于中考常考题型.
四、解答题(本大题共3题,每题8分,满分34分)
24.某药品研究所开发一种抗菌新药,经
( http: / / www.21cnjy.com )多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
【考点】反比例函数的应用;一次函数的应用.
【分析】(1)分别利用正比例函数以及反比例函数解析式求法得出即可;
(2)利用y=4分别得出x的值,进而得出答案.
【解答】解:(1)当0≤x≤4时,设直线解析式为:y=kx,
将(4,8)代入得:8=4k,
解得:k=2,
故直线解析式为:y=2x,
当4≤x≤10时,设反比例函数解析式为:y=,
将(4,8)代入得:8=,
解得:a=32,
故反比例函数解析式为:y=;
因此血液中药物浓度上升阶段的函数关系式为y=2x(0≤x≤4),
下降阶段的函数关系式为y=(4≤x≤10).
(2)当y=4,则4=2x,解得:x=2,
当y=4,则4=,解得:x=8,
∵8﹣2=6(小时),
∴血液中药物浓度不低于4微克/毫升的持续时间6小时.
【点评】此题主要考查了反比例函数的应用,根据题意得出函数解析式是解题关键.
25.2013年,东营市某楼盘以每平方米
( http: / / www.21cnjy.com )6500元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2015年的均价为每平方米5265元.
(1)求平均每年下调的百分率;
(2)假设2016年的均价仍然下调
( http: / / www.21cnjy.com )相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
【考点】一元二次方程的应用.
【专题】增长率问题.
【分析】(1)设平均每年下调的百分率为x,根据题意列出方程,求出方程的解即可得到结果;
(2)如果下调的百分率相同,求出2016年的房价,进而确定出100平方米的总房款,即可做出判断.
【解答】解:(1)设平均每年下调的百分率为x,
根据题意得:6500(1﹣x)2=5265,
解得:x1=0.1=10%,x2=1.9(舍去),
则平均每年下调的百分率为10%;
(2)如果下调的百分率相同,2016年的房价为5265×(1﹣10%)=4738.5(元/米2),
则100平方米的住房总房款为100×4738.5=473850=47.385(万元),
∵20+30>47.385,
∴张强的愿望可以实现.
【点评】此题考查了一元二次方程的应用,找出题中的等量关系是解本题的关键.
26.如图,已知在△ABC中,∠BA
( http: / / www.21cnjy.com )C=90°,AB=AC,点D在边BC上,作∠DAF=90°,且AF=AD,过点F作EF∥AD,且EF=AF,联结CF,CE.
(1)求证:FC⊥BC;
(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.
【考点】全等三角形的判定与性质;线段垂直平分线的性质;等腰直角三角形.
【分析】(1)根据正方形的性质得出AD
( http: / / www.21cnjy.com )=AF,∠FAD=90°=∠BAC,求出∠FAC=∠BAD,证出△ABD≌△ACF,推出∠B=∠FCA即可;
(2)根据△ABD≌△ACF,推出BD=CF=AC,求出∠DAC=∠EFC,根据SAS推出△DAC≌△EFC,即可得出CD=CE.
【解答】解:(1)∵∠BAC=∠DAF=90°,
∴∠BAC﹣∠DAC=∠DAF﹣∠DAC,
即∠BAD=∠CAF,
又∵AB=AC,AD=AF,
∴△ABD≌△ACF,
∴∠B=∠ACF,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠ACF=∠B=45°,
∴∠BCF=90°,
∴FC⊥BC;
(2)∵△ABD≌△ACF,
∴BD=FC,
又∵BD=AC,
∴AC=FC,
∴∠CAF=∠CFA,
∵∠DAF=90°,EF∥AD,
∴∠DAF=∠AFE=90°,
∴∠DAC=∠EFC,
∵AD=AF,EF=AF,
∴AD=FE,
∴△ADC≌△FEC,
∴CD=CE,
∴点C在线段DE的垂直平分线上.
【点评】本题考查了正方形性质,全等三角形的性质和判定,等腰直角三角形性质的应用,主要考查学生综合运用定理进行推理的能力.
27.在△ABC中,AB=A
( http: / / www.21cnjy.com )C,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB;
(3)如图3,将(2)中的
( http: / / www.21cnjy.com )∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交与点F,作DN⊥AC于点N,若DN=FN,(2)中的结论还成立吗?若AB=4,求此时BE的长.
【考点】旋转的性质;等边三角形的判定与性质.
【分析】(1)如图1,易求得∠B=60°,∠BED=90°,BD=2,然后运用三角函数的定义就可求出BE的值;
(2)过点D作DM⊥AB于M,作DN⊥AC
( http: / / www.21cnjy.com )于N,如图2,易证△MBD≌△NCD,则有BM=CN,DM=DN,进而可证到△EMD≌△FND,则有EM=FN,就可得到BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=BC=AB;
(3)过点D作DM⊥AB于M,如图3.同(1
( http: / / www.21cnjy.com ))可得:∠B=∠ACD=60°,同(2)可得:BM=CN,DM=DN,EM=FN.由DN=FN可得DM=DN=FN=EM,从而可得BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM=2BD×sin60°=BC=AB,因为BE+CF=BE+NF﹣CN=BE+DM﹣BM=BE+BD﹣BD=AB,把AB=4,BD=2代入即可得到BE+﹣1=2,从而求得BE=+1.
【解答】解:(1)如图1,
∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∴∠B=∠C=60°,BC=AC=AB=4.
∵点D是线段BC的中点,
∴BD=DC=BC=2.
∵DF⊥AC,即∠AFD=90°,
∴∠AED=360°﹣60°﹣90°﹣120°=90°,
∴∠BED=90°,
∴BE=BD×cos∠B=2×cos60°=2×=1;
(2)过点D作DM⊥AB于M,作DN⊥AC于N,如图2,
则有∠AMD=∠BMD=∠AND=∠CND=90°.
∵∠A=60°,∴∠MDN=360°﹣60°﹣90°﹣90°=120°.
∵∠EDF=120°,∴∠MDE=∠NDF.
在△MBD和△NCD中,
,
∴△MBD≌△NCD,
∴BM=CN,DM=DN.
在△EMD和△FND中,
,
∴△EMD≌△FND,
∴EM=FN,
∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN
=2BM=2BD×cos60°=BD=BC=AB;
(3)过点D作DM⊥AB于M,如图3.
同(1)可得:∠B=∠ACD=60°.
同(2)可得:BM=CN,DM=DN,EM=FN.
∵DN=FN,
∴DM=DN=FN=EM,
∴BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM=2BD×sin60°=BC=AB,
∴(2)中的结论不成立;
∵AB=4,
∴BD=2,
∵BE+CF=BE+NF﹣CN=BE+DM﹣BM=BE+BD﹣BD=AB,
∴BE+﹣1=2,
∴BE=+1.
【点评】本题主要考查了等边三角形的判定与性质
( http: / / www.21cnjy.com )、四边形的内角和定理、全等三角形的判定与性质、三角函数的定义、特殊角的三角函数值等知识,通过证明三角形全等得到BM=CN,DM=DN,EM=FN是解决本题的关键.
同课章节目录
