1.4 直角三角形的射影定理 课件3
文档属性
| 名称 | 1.4 直角三角形的射影定理 课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 197.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-17 11:48:26 | ||
图片预览








文档简介
课件22张PPT。1.4 直角三角形的射影定理【课标要求】
1.理解直角三角形的射影定理.
2.理解直角三角形射影定理的逆定理.
【核心扫描】
用射影定理解决直角三角形的有关问题.(重、难点)自学导引
1.射影的有关概念
(1)点在直线上的正射影:从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的 .
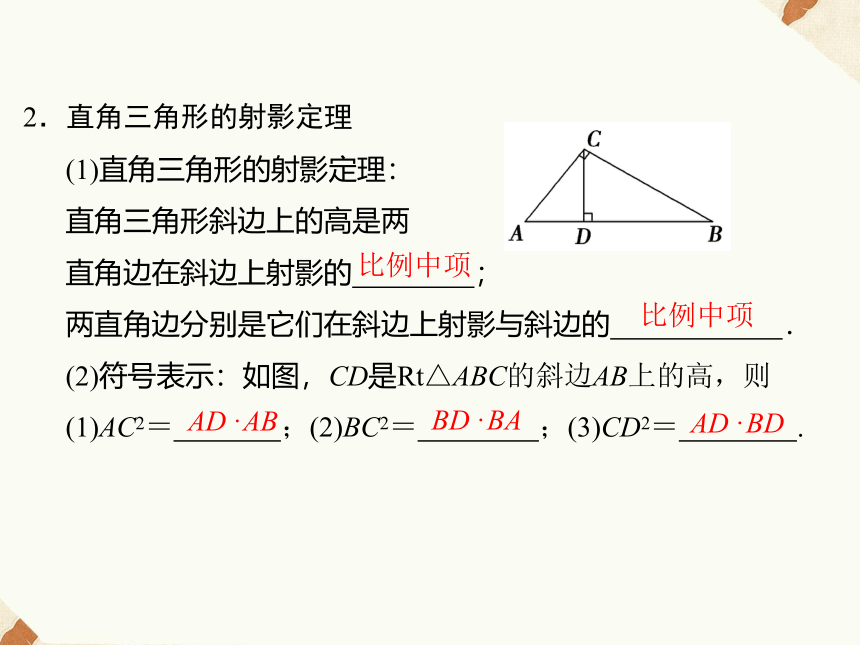
(2)线段在直线上的正射影:一条线段在直线上的正射影,是指线段的两个端点在这条直线上的正射影间的线段.正射影2.直角三角形的射影定理
(1)直角三角形的射影定理:
直角三角形斜边上的高是两
直角边在斜边上射影的 ;
两直角边分别是它们在斜边上射影与斜边的 .
(2)符号表示:如图,CD是Rt△ABC的斜边AB上的高,则(1)AC2= ;(2)BC2= ;(3)CD2= .比例中项比例中项AD·ABBD·BAAD·BD名师点睛
1.应用射影定理有两个条件:一是直角三角形;二是斜边上的高.应用射影定理可求直角三角形的边长、面积等有关量,还可研究相似问题、比例式等问题.2.直角三角形射影定理的逆定理
如果一个三角形一边上的高是另两
边在这条边上的射影的比例中项,
那么这个三角形是直角三角形.
符号表示:如图,在△ABC中,CD⊥AB于D,若CD2=AD·BD,则△ABC为直角三角形.
证明 ∵CD⊥AB,∴∠CDA=∠BDC=90°.又∵CD2=AD·BD,即AD∶CD=CD∶BD∴△ACD∽△CBD.∴∠CAD=∠BCD.又∵∠ACD+∠CAD=90°,∴∠ACB=∠ACD+∠BCD=∠ACD+∠CAD=90°,即△ABC为直角三角形.题型一 射影的概念
【例1】 如图所示,AD⊥BC,FE⊥BC.求点A、B、C、D、E、F、G和线段AB、AC、AF、FG
在直线BC上的射影.
[思维启迪] 要求已知点和线段在直线BC上的射影,需过这些点或线段的端点,作BC边的垂线.解 由AD⊥BC,FE⊥BC知:AD在BC上的射影是D;B在BC上的射影是B;C在BC上的射影是C,E、F、G在BC上的射影都是E;AB在BC上的射影是DB;AC在BC上的射影是DC;AF在BC上的射影是DE,FG在BC上的射影是点E.
反思感悟 求点和线段在直线上的射影
(1)点在直线上的射影就是由点向直线引垂线,垂足即为射影;
(2)线段在直线上的射影就是由线段的两端点向直线引垂线,两垂足间的线段就是所求射影.题型二 射影定理的应用
【例2】 如图所示,在Rt△ABC中,
∠BAC=90°,AD⊥BC于D,
DF⊥AC于F,DE⊥AB于E.
试证明:
(1)AB·AC=AD·BC;
(2)AD3=BC·BE·CF.
[思维启迪] 本题第(1)问是利用△ABC的面积相等求得,在第(2)问中,在Rt△BAC中,有AB·AC=AD·BC,AD2=BD·DC;在Rt△ADB中,有BD2=BE·AB;在Rt△ADC中,有CD2=CF·AC.由这些关系式便可得到待证式.【变式2】 如图,CD是Rt△ABC的斜边AB上的高线.
求证:CD·AC=BC·AD.
证明 在Rt△ABC中,∵CD⊥AB,
∴CD2=BD·AD,BC2=BD·AB,
AC2=AD·AB.
∴CD2·AC2=BD·AB·AD2
=BC2·AD2.∴CD·AC=BC·AD.反思感悟 将困难的、不熟悉的问题转化为容易的、熟悉的问题,体现了化归思想方法,通过恒等变形,找到中间变量来联系前后两个比值,从而达到解题目的.
1.理解直角三角形的射影定理.
2.理解直角三角形射影定理的逆定理.
【核心扫描】
用射影定理解决直角三角形的有关问题.(重、难点)自学导引
1.射影的有关概念
(1)点在直线上的正射影:从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的 .
(2)线段在直线上的正射影:一条线段在直线上的正射影,是指线段的两个端点在这条直线上的正射影间的线段.正射影2.直角三角形的射影定理
(1)直角三角形的射影定理:
直角三角形斜边上的高是两
直角边在斜边上射影的 ;
两直角边分别是它们在斜边上射影与斜边的 .
(2)符号表示:如图,CD是Rt△ABC的斜边AB上的高,则(1)AC2= ;(2)BC2= ;(3)CD2= .比例中项比例中项AD·ABBD·BAAD·BD名师点睛
1.应用射影定理有两个条件:一是直角三角形;二是斜边上的高.应用射影定理可求直角三角形的边长、面积等有关量,还可研究相似问题、比例式等问题.2.直角三角形射影定理的逆定理
如果一个三角形一边上的高是另两
边在这条边上的射影的比例中项,
那么这个三角形是直角三角形.
符号表示:如图,在△ABC中,CD⊥AB于D,若CD2=AD·BD,则△ABC为直角三角形.
证明 ∵CD⊥AB,∴∠CDA=∠BDC=90°.又∵CD2=AD·BD,即AD∶CD=CD∶BD∴△ACD∽△CBD.∴∠CAD=∠BCD.又∵∠ACD+∠CAD=90°,∴∠ACB=∠ACD+∠BCD=∠ACD+∠CAD=90°,即△ABC为直角三角形.题型一 射影的概念
【例1】 如图所示,AD⊥BC,FE⊥BC.求点A、B、C、D、E、F、G和线段AB、AC、AF、FG
在直线BC上的射影.
[思维启迪] 要求已知点和线段在直线BC上的射影,需过这些点或线段的端点,作BC边的垂线.解 由AD⊥BC,FE⊥BC知:AD在BC上的射影是D;B在BC上的射影是B;C在BC上的射影是C,E、F、G在BC上的射影都是E;AB在BC上的射影是DB;AC在BC上的射影是DC;AF在BC上的射影是DE,FG在BC上的射影是点E.
反思感悟 求点和线段在直线上的射影
(1)点在直线上的射影就是由点向直线引垂线,垂足即为射影;
(2)线段在直线上的射影就是由线段的两端点向直线引垂线,两垂足间的线段就是所求射影.题型二 射影定理的应用
【例2】 如图所示,在Rt△ABC中,
∠BAC=90°,AD⊥BC于D,
DF⊥AC于F,DE⊥AB于E.
试证明:
(1)AB·AC=AD·BC;
(2)AD3=BC·BE·CF.
[思维启迪] 本题第(1)问是利用△ABC的面积相等求得,在第(2)问中,在Rt△BAC中,有AB·AC=AD·BC,AD2=BD·DC;在Rt△ADB中,有BD2=BE·AB;在Rt△ADC中,有CD2=CF·AC.由这些关系式便可得到待证式.【变式2】 如图,CD是Rt△ABC的斜边AB上的高线.
求证:CD·AC=BC·AD.
证明 在Rt△ABC中,∵CD⊥AB,
∴CD2=BD·AD,BC2=BD·AB,
AC2=AD·AB.
∴CD2·AC2=BD·AB·AD2
=BC2·AD2.∴CD·AC=BC·AD.反思感悟 将困难的、不熟悉的问题转化为容易的、熟悉的问题,体现了化归思想方法,通过恒等变形,找到中间变量来联系前后两个比值,从而达到解题目的.
