2.3 圆的切线的性质及判定定理 课件3
文档属性
| 名称 | 2.3 圆的切线的性质及判定定理 课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 254.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-17 12:41:17 | ||
图片预览








文档简介
课件26张PPT。2.3 圆的切线的性质及判定定理【课标要求】
1.理解切线的性质定理、判定定理及两个推论,能应用定理及推论解决相关的几何问题.
2.能归纳并正确表述由圆的切线性质定理和两个推论整合而成的定理.
【核心扫描】
1.圆的切线的判定定理、性质定理的理解.(重点)
2.用切线的判定定理、性质定理解决问题.(难点)自学导引
1.圆的切线的性质定理及推论
(1)定理:圆的切线垂直于经过切点的 .
(2)推论1:经过圆心且垂直于切线的直线必经过 .
(3)推论2:经过切点且垂直于切线的直线必经过 .半径切点圆心推敲引申:(1)本定理及其两个推
论可以用一个定理叙述出来,即:
如果圆的一条直线满足以下三个
条件中的任意两条,那么就一定
满足第三条.它们是:①垂直于切线;②过切点;③过圆心.
(2)本定理题设为:一条直线既过圆心又过切点,结论为:这条直线与圆的切线垂直.如图所示,若直线l切⊙O于A,直线l′经过点O、A,则直线l′⊥l.2.圆的切线的判定定理
(1)判定定理:经过半径的外端并且垂直于 的直线是圆的切线.
(2)圆的切线的判断方法这条半径推敲引申:(1)圆的切线的判定定理还可表述为:如果一条直线经过圆的一条半径的外端点,并且垂直于这条半径,那么这条直线就是这个圆的切线.
(2)判断一条直线是否是切线的三种方法中:②③是由①推出的;②是用数量关系来判断;③是用位置关系来判断.名师点睛
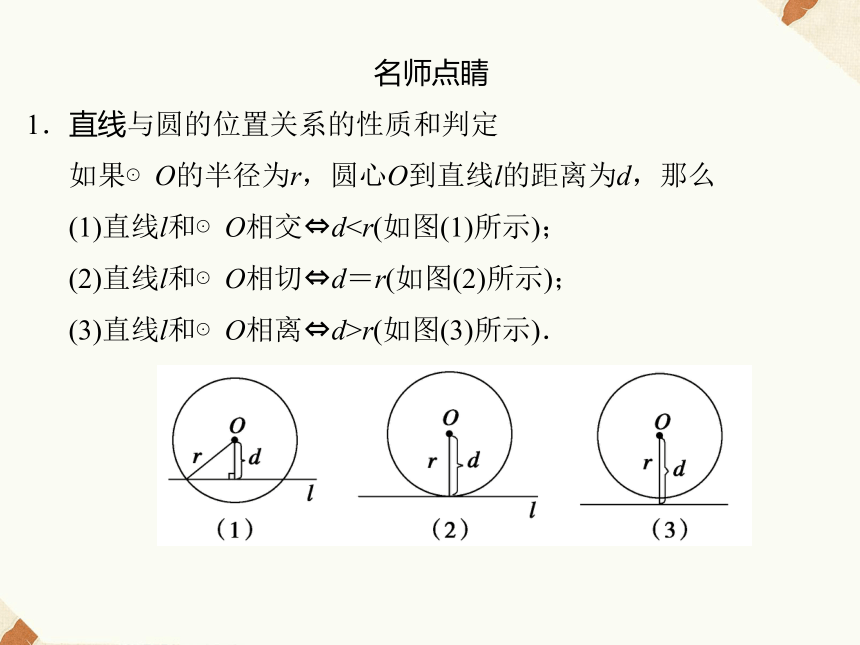
1.直线与圆的位置关系的性质和判定
如果⊙O的半径为r,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交?d (2)直线l和⊙O相切?d=r(如图(2)所示);
(3)直线l和⊙O相离?d>r(如图(3)所示).说明:(1)命题左边反映的是两个图形(直线和圆)的位置关系,右边反映的是两个数量的大小关系.
(2)对于两个图形(直线l和⊙O)的位置关系,或两个数(d和r)的大小关系,有且仅有一种情况是成立的.
(3)从左端推出右端是直线和圆的位置关系的性质,从右端推出左端是直线和圆的位置关系的判定.2.圆的切线的性质与判定的综合运用
在解决有关圆的切线问题(无论是计算还是证明)时,通常需要添加辅助线.一般地,添加辅助线有以下规律:
(1)已知一条直线是圆的切线时,通常连接圆心和切点,这条半径垂直于切线.
(2)要证明某条直线是圆的切线时,若已知直线经过圆上的某一点,则需作出经过这一点的半径,证明直线垂直于这条半径,简记为“连半径,证垂直”;若直线与圆的公共点没有确定,则应过圆心作直线的垂线,得到垂线段,再证明这条垂线段的长等于半径,简记为“作垂直,证半径”.题型一 圆的切线的判断
【例1】 如图所示,在△ABC中,
已知AB=AC,以AB为直径的
⊙O交BC于点D,DE⊥AC于
点E.
求证:DE是⊙O的切线.
[思维启迪] 利用圆的切线的判定定理进行切线的证明,关键是找出定理的两个条件:①过半径的外端;②该直线与某一条半径所在的直线垂直.证明 连接OD和AD,如图所示.
∵AB是⊙O的直径,∴AD⊥BC.
∵AB=AC,∴BD=CD.∵AO=OB,∴OD∥AC.
∵DE⊥AC,∴DE⊥OD,∴DE是⊙O的切线.
反思感悟 判断一条直线是圆的切线时,常用辅助线的作法
①如果已知这条直线与圆有公共点,则连接圆心与这个公共点,设法证明连接所得到的半径与这条直线垂直,简记为“连半径,证垂直”;
②若题目未说明这条直线与圆有公共点,则过圆心作这条直线的垂线,得垂线段,再证明这条垂线段的长等于半径,简记“作垂直,证半径”.【变式1】 如图所示,在梯形ABCD中,AD∥BC,∠C=90°,且AD+BC=AB,AB为⊙O的直径.
求证:⊙O与CD相切.题型二 圆的切线性质定理的应用
【例2】 如图所示,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,
过Q作⊙O的切线交OA的延长线于R,
求证:RP=RQ.
[思维启迪] 已知QR是⊙O的切线,可利用切线的性质定理,即OQ⊥RQ.另外,要证RP=RQ,只要证∠RPQ=∠RQP即可,只要证∠BPO=∠PQR即可,再结合OQ⊥RQ.证明 连接OQ.因为QR是⊙O的切线,所以OQ⊥QR.
因为OB=OQ,所以∠B=∠OQB.
因为BO⊥OA,
所以∠BPO=90°-∠B=∠RPQ,
∠PQR=90°-∠OQP.
所以∠RPQ=∠PQR.
所以RP=RQ.
反思感悟 题目中若有圆的切线,首先可以连接圆心和切点,出现垂直关系.【变式2】 如图所示,在⊙O中,AB是⊙O的直径,AD是弦,过点B的切线与AD的延长线交于点C,且AD=DC,求∠ABD的度数.
解 ∵BC是⊙O的切线,
∴AB⊥BC.
∴△ABC是直角三角形.
∵CD=AD,∴BD=AD.
∵AB是⊙O的直径,
∴AD⊥BD.
∴△ABD是等腰直角三角形.
∴∠ABD=45°.反思感悟 (1)用切线的性质定理求解线段的长度时,应注意的问题
①观察图形,作辅助线;
②利用相关知识,如圆周角定理、圆的切线性质定理、判定定理等.
(2)在应用切线的性质定理及其推论进行几何证明和求解时,如果已知切点,则连接圆心和切点构成垂直是一种常用的方法.方法技巧 圆内接四边形与圆的切线综合的求解策略
【示例1】 如图所示,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.
(1)证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小.(1)证明 连接OP,OM,
因为AP与⊙O相切于点P,所以OP⊥AP.
因为M是⊙O的弦BC的中点,所以OM⊥BC.
于是∠OPA+∠OMA=180°,
由圆心O在∠PAC的内部,
可知四边形APOM的对角互补,
所以A,P,O,M四点共圆. (2)解 由(1)得,A,P,O,M四点共圆,
所以∠OAM=∠OPM.
由(1)得OP⊥AP.
由圆心O在∠PAC的内部,
可知∠OPM+∠APM=90°,
所以∠OAM+∠APM=90°.
1.理解切线的性质定理、判定定理及两个推论,能应用定理及推论解决相关的几何问题.
2.能归纳并正确表述由圆的切线性质定理和两个推论整合而成的定理.
【核心扫描】
1.圆的切线的判定定理、性质定理的理解.(重点)
2.用切线的判定定理、性质定理解决问题.(难点)自学导引
1.圆的切线的性质定理及推论
(1)定理:圆的切线垂直于经过切点的 .
(2)推论1:经过圆心且垂直于切线的直线必经过 .
(3)推论2:经过切点且垂直于切线的直线必经过 .半径切点圆心推敲引申:(1)本定理及其两个推
论可以用一个定理叙述出来,即:
如果圆的一条直线满足以下三个
条件中的任意两条,那么就一定
满足第三条.它们是:①垂直于切线;②过切点;③过圆心.
(2)本定理题设为:一条直线既过圆心又过切点,结论为:这条直线与圆的切线垂直.如图所示,若直线l切⊙O于A,直线l′经过点O、A,则直线l′⊥l.2.圆的切线的判定定理
(1)判定定理:经过半径的外端并且垂直于 的直线是圆的切线.
(2)圆的切线的判断方法这条半径推敲引申:(1)圆的切线的判定定理还可表述为:如果一条直线经过圆的一条半径的外端点,并且垂直于这条半径,那么这条直线就是这个圆的切线.
(2)判断一条直线是否是切线的三种方法中:②③是由①推出的;②是用数量关系来判断;③是用位置关系来判断.名师点睛
1.直线与圆的位置关系的性质和判定
如果⊙O的半径为r,圆心O到直线l的距离为d,那么
(1)直线l和⊙O相交?d
(3)直线l和⊙O相离?d>r(如图(3)所示).说明:(1)命题左边反映的是两个图形(直线和圆)的位置关系,右边反映的是两个数量的大小关系.
(2)对于两个图形(直线l和⊙O)的位置关系,或两个数(d和r)的大小关系,有且仅有一种情况是成立的.
(3)从左端推出右端是直线和圆的位置关系的性质,从右端推出左端是直线和圆的位置关系的判定.2.圆的切线的性质与判定的综合运用
在解决有关圆的切线问题(无论是计算还是证明)时,通常需要添加辅助线.一般地,添加辅助线有以下规律:
(1)已知一条直线是圆的切线时,通常连接圆心和切点,这条半径垂直于切线.
(2)要证明某条直线是圆的切线时,若已知直线经过圆上的某一点,则需作出经过这一点的半径,证明直线垂直于这条半径,简记为“连半径,证垂直”;若直线与圆的公共点没有确定,则应过圆心作直线的垂线,得到垂线段,再证明这条垂线段的长等于半径,简记为“作垂直,证半径”.题型一 圆的切线的判断
【例1】 如图所示,在△ABC中,
已知AB=AC,以AB为直径的
⊙O交BC于点D,DE⊥AC于
点E.
求证:DE是⊙O的切线.
[思维启迪] 利用圆的切线的判定定理进行切线的证明,关键是找出定理的两个条件:①过半径的外端;②该直线与某一条半径所在的直线垂直.证明 连接OD和AD,如图所示.
∵AB是⊙O的直径,∴AD⊥BC.
∵AB=AC,∴BD=CD.∵AO=OB,∴OD∥AC.
∵DE⊥AC,∴DE⊥OD,∴DE是⊙O的切线.
反思感悟 判断一条直线是圆的切线时,常用辅助线的作法
①如果已知这条直线与圆有公共点,则连接圆心与这个公共点,设法证明连接所得到的半径与这条直线垂直,简记为“连半径,证垂直”;
②若题目未说明这条直线与圆有公共点,则过圆心作这条直线的垂线,得垂线段,再证明这条垂线段的长等于半径,简记“作垂直,证半径”.【变式1】 如图所示,在梯形ABCD中,AD∥BC,∠C=90°,且AD+BC=AB,AB为⊙O的直径.
求证:⊙O与CD相切.题型二 圆的切线性质定理的应用
【例2】 如图所示,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,
过Q作⊙O的切线交OA的延长线于R,
求证:RP=RQ.
[思维启迪] 已知QR是⊙O的切线,可利用切线的性质定理,即OQ⊥RQ.另外,要证RP=RQ,只要证∠RPQ=∠RQP即可,只要证∠BPO=∠PQR即可,再结合OQ⊥RQ.证明 连接OQ.因为QR是⊙O的切线,所以OQ⊥QR.
因为OB=OQ,所以∠B=∠OQB.
因为BO⊥OA,
所以∠BPO=90°-∠B=∠RPQ,
∠PQR=90°-∠OQP.
所以∠RPQ=∠PQR.
所以RP=RQ.
反思感悟 题目中若有圆的切线,首先可以连接圆心和切点,出现垂直关系.【变式2】 如图所示,在⊙O中,AB是⊙O的直径,AD是弦,过点B的切线与AD的延长线交于点C,且AD=DC,求∠ABD的度数.
解 ∵BC是⊙O的切线,
∴AB⊥BC.
∴△ABC是直角三角形.
∵CD=AD,∴BD=AD.
∵AB是⊙O的直径,
∴AD⊥BD.
∴△ABD是等腰直角三角形.
∴∠ABD=45°.反思感悟 (1)用切线的性质定理求解线段的长度时,应注意的问题
①观察图形,作辅助线;
②利用相关知识,如圆周角定理、圆的切线性质定理、判定定理等.
(2)在应用切线的性质定理及其推论进行几何证明和求解时,如果已知切点,则连接圆心和切点构成垂直是一种常用的方法.方法技巧 圆内接四边形与圆的切线综合的求解策略
【示例1】 如图所示,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点.
(1)证明:A、P、O、M四点共圆;
(2)求∠OAM+∠APM的大小.(1)证明 连接OP,OM,
因为AP与⊙O相切于点P,所以OP⊥AP.
因为M是⊙O的弦BC的中点,所以OM⊥BC.
于是∠OPA+∠OMA=180°,
由圆心O在∠PAC的内部,
可知四边形APOM的对角互补,
所以A,P,O,M四点共圆. (2)解 由(1)得,A,P,O,M四点共圆,
所以∠OAM=∠OPM.
由(1)得OP⊥AP.
由圆心O在∠PAC的内部,
可知∠OPM+∠APM=90°,
所以∠OAM+∠APM=90°.
