1.2 平行线分线段成比例定理 教案
文档属性
| 名称 | 1.2 平行线分线段成比例定理 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 410.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-17 12:05:27 | ||
图片预览


文档简介
1.2
平行线分线段成比例定理
教案
教学目标
1.使学生理解平行线分线段成比例定理及其初步证明;
2.使学生初步熟悉平行线分线段成比例定理的用途、用法;
3.通过定理的教学,培养学生的联想能力、概括能力.
教学重、难点
重点:取得“猜想”的认识过程,以及论证思路的寻求过程.
难点:成比例的线段中,对应线段的确认.
教学过程
(一)旧知识的复习
利用投影仪提出下列各题使学生解答.
1.求出下列各式中的x:y.
(1)3x=5y;
(2)x=;
(3)3:2=:;
(4)3:=5:.
2.已知.
3.已知.
其中第1题以学生分别口答、共同核对的方式进行;第2、3题以学生各自解答,指定2人板演,而后共同核对板演所述,并追问理论根据的方式进行.
(二)新知识的教学
1.提出问题,使学生思考.
在已学过的定理中,有没有包含两条线段的比是1:1的?
而后使学生试答,如果答出定理——过三角形一边的中点与另一边平行的直线,必平分第三边,那么追问理由,如果答不出,那么利用图1(若E是AB中点,EF//BC,交AC于F点,则AF=FC)使学生观察,并予以分析而得出,并指出此定理也可谓:如果E是△ABC的AB边上一点,且,EF//BC交AC于F点,那么.
2.引导学生探索与讨论.
就着上述结论提出,在△ABC中,EF//BC这个条件不变,但不等于,譬如=时,应等于“几比几”?并使学生各自画图、进行度量,得出“猜想”——配合着黑板上画出的相应图观察、明确.
而后使学生试证,如能证明,则让学生进行证明,并明确论证的理论根据,如果学生不会证明,那么以“可否类比着平行线等分线段定理的证法?”引导,而后指定学生进行证明.
继而再问学生,是否还有包含线段的比是1:1的定理,学生答出定理——过梯形一腰的中点与底平行的直线,平分另一腰后,画出相应的图(图2),并随即提出问题:
在梯形ABCD中,EF//BC的条件不变,但E不是AB的中点,仍如=,那么是否也等于?
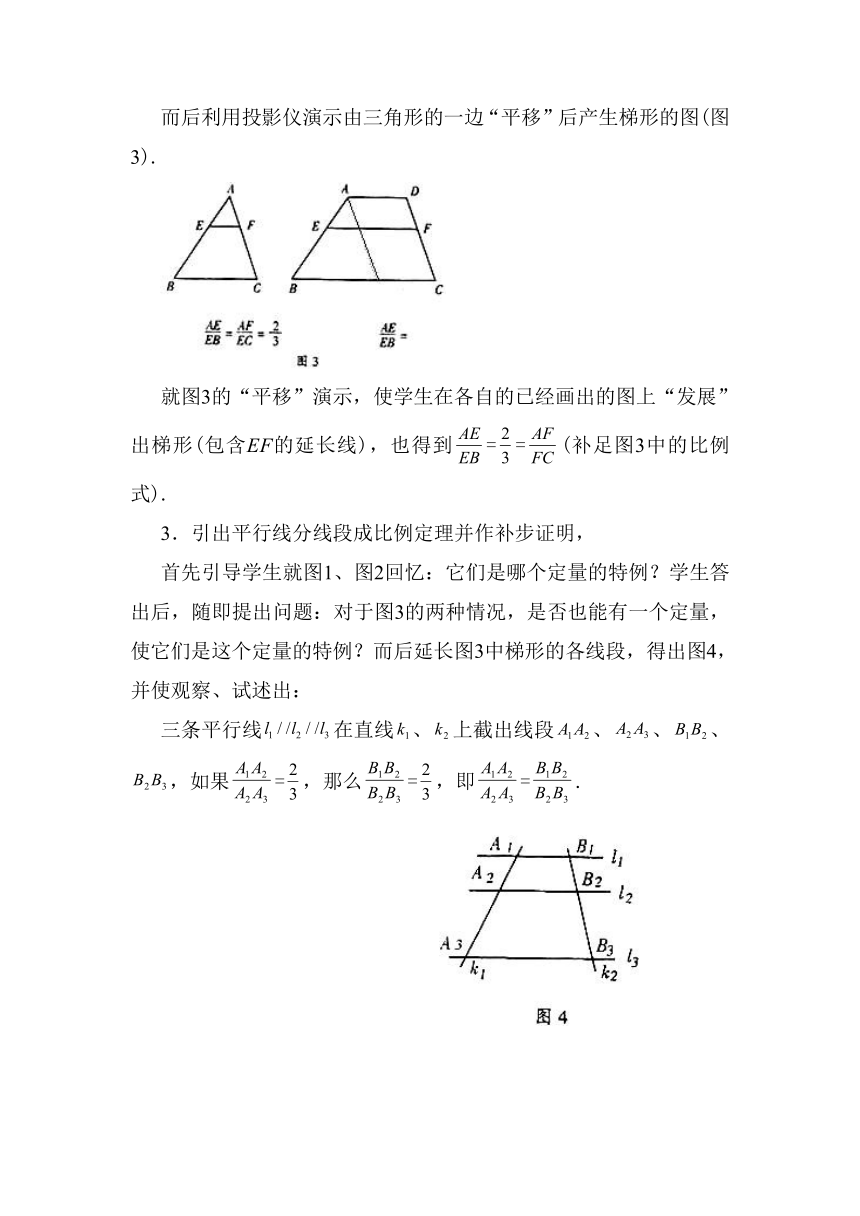
而后利用投影仪演示由三角形的一边“平移”后产生梯形的图(图3).
就图3的“平移”演示,使学生在各自的已经画出的图上“发展”出梯形(包含EF的延长线),也得到==(补足图3中的比例式).
3.引出平行线分线段成比例定理并作补步证明,
首先引导学生就图1、图2回忆:它们是哪个定量的特例?学生答出后,随即提出问题:对于图3的两种情况,是否也能有一个定量,使它们是这个定量的特例?而后延长图3中梯形的各线段,得出图4,并使观察、试述出:
三条平行线在直线、上截出线段、、、,如果=,那么=,即=.
继而使学生仿照前面的证明,证明这个情况.
进一步提出:=(m、n为自然数),那么怎样证明=?并使学生试证,并概括为:
三条平行线在直线、上截出线段、、、,那么=.
在此基础上,教师提出问题:由=,利用比例的性质还可得到哪些比例式?(=,=,等)
引导学生回忆平行线等分线段定理所包含的各种情况,并类比着使学生说出定理所包含的各种情况,而后投影出,并指出分类的标准.
最后,使学生类比着平行线等分线段定理的叙述,试述此定理.
平行线分线段对应成比例定理
三条平行线截两条直线,所得的对应线段成比例.
观察下图,l与l′的交点分别在l1、l2上.根据平行线分线段成比例定理,可得:
如果把图中的直线l2看成是平行于△ABC的BC边的直线,那么可以得到:
推论
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
(三)例题解析
例1
如图,在△ABC中,DE//BC,DF//AC,AE=4,EC=2,BC=8.求BF和CF的长.
解:
由(1)(2)式得:
例2
如图,在△ABC中,DE//BC,EF//CD.求证:AD是AB和AF的比例中项.
证明:在△ABC中,∵DE//BC,
在△ADC中,∵EF//CD,
由(1)(2)式得
∴AD2=AB×AF,即AD是AB和AF的比例中项.
例3
用平行于三角形一边且和其他两边相交的直线截三角形的三边与原三角形的三边对应成比例.
已知:如图,DE//BC,DE分别交AB、AC于点D、E.
求证:
证明:过点E作EF//AB,交BC于点F,
且
四边形DEFB为平行四边形.
(四)小结
1.本节课在平行线等分线段定理的基础上,学行线分线段成比例定理,平行线等分线段定理是平行线分线段成比例定理的特殊情况,“证明”平行线分线段成比例定理是通过转化为平行线等分线段定理来解决的.
2.使用平行线分线段成比例定理时,一要看清平行线组;二要找准平行线组截得的对应线段,否则就会产生错误.
平行线分线段成比例定理
教案
教学目标
1.使学生理解平行线分线段成比例定理及其初步证明;
2.使学生初步熟悉平行线分线段成比例定理的用途、用法;
3.通过定理的教学,培养学生的联想能力、概括能力.
教学重、难点
重点:取得“猜想”的认识过程,以及论证思路的寻求过程.
难点:成比例的线段中,对应线段的确认.
教学过程
(一)旧知识的复习
利用投影仪提出下列各题使学生解答.
1.求出下列各式中的x:y.
(1)3x=5y;
(2)x=;
(3)3:2=:;
(4)3:=5:.
2.已知.
3.已知.
其中第1题以学生分别口答、共同核对的方式进行;第2、3题以学生各自解答,指定2人板演,而后共同核对板演所述,并追问理论根据的方式进行.
(二)新知识的教学
1.提出问题,使学生思考.
在已学过的定理中,有没有包含两条线段的比是1:1的?
而后使学生试答,如果答出定理——过三角形一边的中点与另一边平行的直线,必平分第三边,那么追问理由,如果答不出,那么利用图1(若E是AB中点,EF//BC,交AC于F点,则AF=FC)使学生观察,并予以分析而得出,并指出此定理也可谓:如果E是△ABC的AB边上一点,且,EF//BC交AC于F点,那么.
2.引导学生探索与讨论.
就着上述结论提出,在△ABC中,EF//BC这个条件不变,但不等于,譬如=时,应等于“几比几”?并使学生各自画图、进行度量,得出“猜想”——配合着黑板上画出的相应图观察、明确.
而后使学生试证,如能证明,则让学生进行证明,并明确论证的理论根据,如果学生不会证明,那么以“可否类比着平行线等分线段定理的证法?”引导,而后指定学生进行证明.
继而再问学生,是否还有包含线段的比是1:1的定理,学生答出定理——过梯形一腰的中点与底平行的直线,平分另一腰后,画出相应的图(图2),并随即提出问题:
在梯形ABCD中,EF//BC的条件不变,但E不是AB的中点,仍如=,那么是否也等于?
而后利用投影仪演示由三角形的一边“平移”后产生梯形的图(图3).
就图3的“平移”演示,使学生在各自的已经画出的图上“发展”出梯形(包含EF的延长线),也得到==(补足图3中的比例式).
3.引出平行线分线段成比例定理并作补步证明,
首先引导学生就图1、图2回忆:它们是哪个定量的特例?学生答出后,随即提出问题:对于图3的两种情况,是否也能有一个定量,使它们是这个定量的特例?而后延长图3中梯形的各线段,得出图4,并使观察、试述出:
三条平行线在直线、上截出线段、、、,如果=,那么=,即=.
继而使学生仿照前面的证明,证明这个情况.
进一步提出:=(m、n为自然数),那么怎样证明=?并使学生试证,并概括为:
三条平行线在直线、上截出线段、、、,那么=.
在此基础上,教师提出问题:由=,利用比例的性质还可得到哪些比例式?(=,=,等)
引导学生回忆平行线等分线段定理所包含的各种情况,并类比着使学生说出定理所包含的各种情况,而后投影出,并指出分类的标准.
最后,使学生类比着平行线等分线段定理的叙述,试述此定理.
平行线分线段对应成比例定理
三条平行线截两条直线,所得的对应线段成比例.
观察下图,l与l′的交点分别在l1、l2上.根据平行线分线段成比例定理,可得:
如果把图中的直线l2看成是平行于△ABC的BC边的直线,那么可以得到:
推论
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
(三)例题解析
例1
如图,在△ABC中,DE//BC,DF//AC,AE=4,EC=2,BC=8.求BF和CF的长.
解:
由(1)(2)式得:
例2
如图,在△ABC中,DE//BC,EF//CD.求证:AD是AB和AF的比例中项.
证明:在△ABC中,∵DE//BC,
在△ADC中,∵EF//CD,
由(1)(2)式得
∴AD2=AB×AF,即AD是AB和AF的比例中项.
例3
用平行于三角形一边且和其他两边相交的直线截三角形的三边与原三角形的三边对应成比例.
已知:如图,DE//BC,DE分别交AB、AC于点D、E.
求证:
证明:过点E作EF//AB,交BC于点F,
且
四边形DEFB为平行四边形.
(四)小结
1.本节课在平行线等分线段定理的基础上,学行线分线段成比例定理,平行线等分线段定理是平行线分线段成比例定理的特殊情况,“证明”平行线分线段成比例定理是通过转化为平行线等分线段定理来解决的.
2.使用平行线分线段成比例定理时,一要看清平行线组;二要找准平行线组截得的对应线段,否则就会产生错误.
