1.4 直角三角形的射影定理 教案
文档属性
| 名称 | 1.4 直角三角形的射影定理 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 128.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-17 12:09:44 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.4
直角三角形的射影定理
教案
教学目标
知识与技能:掌握直角三角形中成比例的线段的性质,并能初步用它解决“直角三角形斜边上的高”图形中的计算和证明问题.
方法与过程:
通过问题设计,层层跟进,引导学生探索和发现射影定理.
情感与价值观:培养特殊化研究问题的方法和方程、转化思想.
教学重难点
重点:直角三角形的射影定理的证明及应用;
难点:直角三角形的射影定理的证明.
教学过程
一、教学引入
什么是射影?
点和线段的正射影简称为射影
(让学生复习并挖掘下图中的基本性质.)
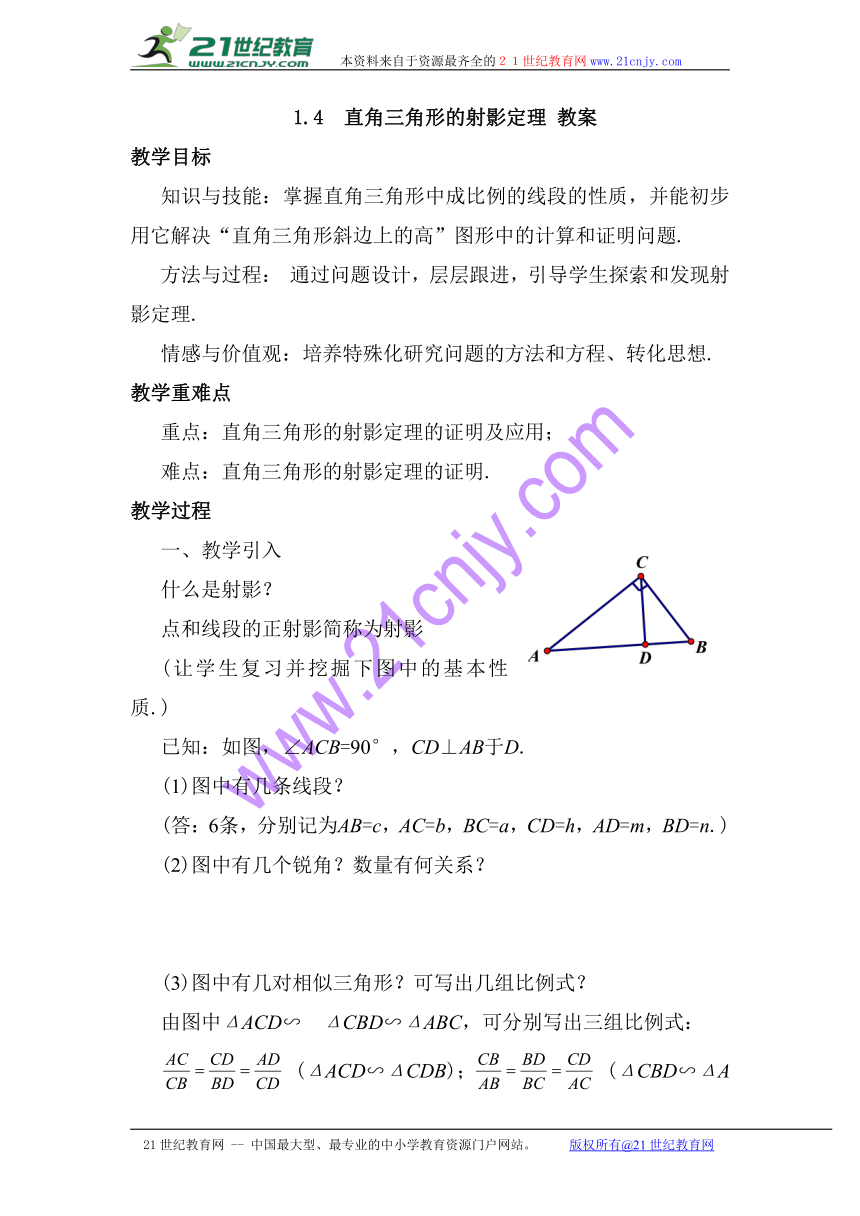
已知:如图,∠ACB=90°,CD⊥AB于D.
(1)图中有几条线段?
(答:6条,分别记为AB=c,AC=b,BC=a,CD=h,AD=m,BD=n.)
(2)图中有几个锐角?数量有何关系?
(3)图中有几对相似三角形?可写出几组比例式?
由图中ΔACD?∽ΔCBD∽ΔABC,可分别写出三组比例式:
(ΔACD∽ΔCDB);
(ΔCBD∽ΔABC);
(ΔACD∽ΔABC).
(4)观察第(3)题的结果,有几个带有比例中项的比例式?如何用一句话概括叙述这几个比例中项的表达式?21教育网
只有三个比例中项的表达式,,,
(5)由上可得到哪些等积式?
CD2=AD·BD,BC2=BD·BA,AC2=AD·AB
总结得:
射影定理
直角三角形斜边上的高是两直角边在斜边上的射影的比例中项;两直角边分别是它们在斜边上的射影与斜边的比例中项.21cnjy.com
请同学们自己写出已知条件并证明.
已知:在RT△ABC中,∠ABC=90°,CD⊥AB于D.
求证:CD2=ADBD、BC2=BDAB、AC2=ADAB
证明:在RT△ABC中,因为∠ABC=90.
CD⊥AB
∠B+∠DCB=90
,
∠ACD+∠DCB=90
所以∠B=∠ACD,故
△CBD∽△ACD
所以
在RT△ACB与RT△BDC中,为公共角,
∽
同理,由∽,
讨论:
用勾股定理能证明射影定理吗?写出你的想法.
证明:
二、例题解析
例1
如图1-35(课本第21页),圆O上一点C在直径AB上的射影为D.求CD、AC和BC的长.
21世纪教育网版权所有
例2
如图1-36(课本第22页),ΔABC中,顶点C在AB边上的射影为D,且.
求证:ΔABC是直角三角形.
三、课堂小结与反思
学会利用射影定理解相关问题.
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
1.4
直角三角形的射影定理
教案
教学目标
知识与技能:掌握直角三角形中成比例的线段的性质,并能初步用它解决“直角三角形斜边上的高”图形中的计算和证明问题.
方法与过程:
通过问题设计,层层跟进,引导学生探索和发现射影定理.
情感与价值观:培养特殊化研究问题的方法和方程、转化思想.
教学重难点
重点:直角三角形的射影定理的证明及应用;
难点:直角三角形的射影定理的证明.
教学过程
一、教学引入
什么是射影?
点和线段的正射影简称为射影
(让学生复习并挖掘下图中的基本性质.)
已知:如图,∠ACB=90°,CD⊥AB于D.
(1)图中有几条线段?
(答:6条,分别记为AB=c,AC=b,BC=a,CD=h,AD=m,BD=n.)
(2)图中有几个锐角?数量有何关系?
(3)图中有几对相似三角形?可写出几组比例式?
由图中ΔACD?∽ΔCBD∽ΔABC,可分别写出三组比例式:
(ΔACD∽ΔCDB);
(ΔCBD∽ΔABC);
(ΔACD∽ΔABC).
(4)观察第(3)题的结果,有几个带有比例中项的比例式?如何用一句话概括叙述这几个比例中项的表达式?21教育网
只有三个比例中项的表达式,,,
(5)由上可得到哪些等积式?
CD2=AD·BD,BC2=BD·BA,AC2=AD·AB
总结得:
射影定理
直角三角形斜边上的高是两直角边在斜边上的射影的比例中项;两直角边分别是它们在斜边上的射影与斜边的比例中项.21cnjy.com
请同学们自己写出已知条件并证明.
已知:在RT△ABC中,∠ABC=90°,CD⊥AB于D.
求证:CD2=ADBD、BC2=BDAB、AC2=ADAB
证明:在RT△ABC中,因为∠ABC=90.
CD⊥AB
∠B+∠DCB=90
,
∠ACD+∠DCB=90
所以∠B=∠ACD,故
△CBD∽△ACD
所以
在RT△ACB与RT△BDC中,为公共角,
∽
同理,由∽,
讨论:
用勾股定理能证明射影定理吗?写出你的想法.
证明:
二、例题解析
例1
如图1-35(课本第21页),圆O上一点C在直径AB上的射影为D.求CD、AC和BC的长.
21世纪教育网版权所有
例2
如图1-36(课本第22页),ΔABC中,顶点C在AB边上的射影为D,且.
求证:ΔABC是直角三角形.
三、课堂小结与反思
学会利用射影定理解相关问题.
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
