第三章第二节,逻辑门课件
图片预览











文档简介
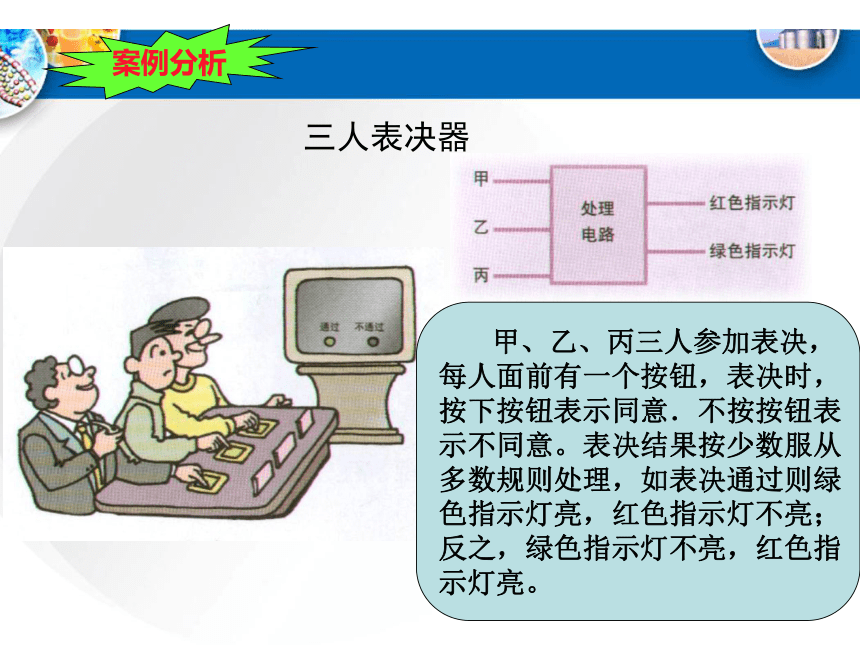
课件41张PPT。第三章电子控制系统的信号处理三种基本的逻辑门与非门和或非门第二节 逻辑门案例分析三人表决器 甲、乙、丙三人参加表决,每人面前有一个按钮,表决时,按下按钮表示同意.不按按钮表示不同意。表决结果按少数服从多数规则处理,如表决通过则绿色指示灯亮,红色指示灯不亮;反之,绿色指示灯不亮,红色指示灯亮。 电子控制系统控制(处理)部分的输出信号与输入信号之间存在着一定的逻辑关系,其中输出信号对应于逻辑结论,输入信号对应于逻辑前提。
电子控制系统的控制(处理)部分于是依据各输出信号与输入信号之间的逻辑关系(因果关系)来处理的。为处理方便,将逻辑前提和逻辑结论均用字母A、B、C等表示,显然,这些字母都应当只有“真”和“假”两个状态,且非真即假,非假即真。
实现各种逻辑关系的电路称为数字电路(或逻辑电路)。在数字电路中,“真”用高电平(“1”)表示,“假”用低电平(“0”)表示。“1”和“0”称为数字电路的真值或逻辑值。三种基本的逻辑门 任何复杂的逻辑关系都由“与”、“或”、“非”三种基本逻辑关系组合而成,实现这三种基本逻辑关系的电路分别称为与门(AND)、或门(OR)和非门(NOT),它们的输入信号代表逻辑前提,输出信号代表逻辑结论。思考 请列举在日常生活中常见的与逻辑有关系的例子 与逻辑关系举例:
1.火车在开动时,所有车门必须关好,如有车门没关不能放行。
2.我国婚姻法规定,男女双方必须同时到场方可登记结婚。
3.开学时班长宜布班级活动计划:三月份将选择一个晴朗的星期六去郊游。
4.小明家走廊上有一盏节能路灯,天黑以后,有人通过并发出响声时,灯才亮,其他情况下灯不亮。
5.仓库的门通常用两把锁,由不同的人保管,开门时必须两个保管人同时到场。与门“所有逻辑前提皆为真时,逻辑结论才为真”的逻辑关系称为“与”逻辑关系。(1)什么是与门?
——实现与逻辑关系的电路称为与门。1、与门 开关串联电路 两只开关控制一盏灯亮和灭的电路,在真值表内 填入灯亮与否的情况。 真值表 若令开关通为真,断为假;灯亮为真,不亮为假,请判断该电路是否为与逻辑关系。(2)与门电路的特点:
只有当与门的所有输入端皆为高电平“1”时,输出端才为高电平“1”。即“全高出高,有低出低” 特点:
“全高出高,有低出低”
(3)与逻辑关系在布尔代数中定义为逻辑乘法,记作:F=A*B F=A.B F=AB(4)与逻辑符号 数字电路的逻辑关系常常用波形图来描述,波形图记录门电路的输人信号或输出信号的电子随时间变化的情况,如右图所示。 右图小的与门在A和B两个波形的输入电压的作用下,得到如F波形所示的输出电压。第二节 逻辑门 在画波形图时,常常省去坐标轴,但输入波形与输出波形之间的时间必须严格对应,如下图中虚线所示。图中第三个时间区间,输入A和输入B都为1,符合“全高出高”规则,因而输出F也为1,其他情况不符合,因而输出为0。与门的输入、输出波形图“全高出高,有低出低”F马上行动“全高出高,有低出低”思 考“全高出高,有低出低” 或逻辑关系举例:
1.暑假里,高二(3)班同学一起到青岛去旅游。从上海到青岛可以乘火车、汽车,飞机,还可以乘海轮。
2 .高二(1)班教室有3把钥匙,班主任1把,班长1把,值日生1把,谁先到校都可以开门。
3.小明家楼顶的水箱通常在天黑以后进水,但若白天水箱的水用完了也能进水。
4.班主任通知开家长会时要求:父亲来可以,母亲来也可以,父母一起来更好。或门 “逻辑前提中有一个或一个以上为真,逻辑结论就为真”的逻辑关系称为“或”逻辑关系。例如,到图书馆借书,可以凭本校学生证也可以凭借书证,两证中有一个即可,这里的逻辑关系就是或逻辑关系。 请列举在日常生活中常见的或逻辑有关系的例子第二节 逻辑门ALB断通真值表断断断通通断通通通通马上行动两只开关控制一盏灯亮和灭的电路,在真值表内填入灯亮与否的情况。
(1)“逻辑前提中有一个或一个以上为真,逻辑结论就为真”
即:“见高出高,全低出低”
(2)或逻辑关系在布尔代数中定义为逻辑加法,记作: F=A+B
(3)实现或逻辑关系的电路称为或门。
(并联开关电路)2、或门(4)或逻辑关系符号马上行动 列出3个输入端的或门真值表,并画出输出波形“见高出高,全低出低” “逻辑前提为假时逻辑结论为真,逻辑前提为真时逻辑结论反而为假”,即逻辑结论与逻辑前提的逻辑值总是相反的逻辑关系称为非逻辑关系。记作:F = A读作“A非”。非逻辑关系的真值表如下表所示。从真值表可以看出:
0 = 1, 1 = 0 非门
F = A 非逻辑的例子如机场或车站旅客入口处要进行安全检查,带有易燃易爆物品者不得入内。第二节 逻辑门(1)“逻辑前提为假时逻辑结论为真,逻辑结论为真时逻辑结论反而为假”3、非门逻辑结论与逻辑前提的逻辑值总是相反.记作:(2)实现非逻辑关系的电路称为非门。(3)非门逻辑符号即:“见高出低,见低出高 ” 若以体温低于38℃为逻辑前提,则此逻辑前提与进单位办公和进观察室检查这两个逻辑结论之间,哪一个符合非逻辑关系?思考案例分析 “非典”流行时期,某单位的工作人员进单位办公均必须测体温,若体温超过38℃,则不能进入单位办公,且要进入观察室接受其他检查。这里,体温超过38℃ ,是逻辑前提,进单位办公和进观察室检查是两个逻辑结论,进单位办公与体温超过38℃之间是非逻辑关系,而进观察室检查与体温超过38℃之间则不是非逻辑关系。第二节 逻辑门ALR真值表马上行动 下图是描述非逻辑关系的示意图。请说明在上述案例中.应对逻辑前提A的逻辑结论L的真和假如何规定,才能符合非逻辑关系的定义?为什么? A:开关合上为真;
L:灯亮为真。
因为开关合上时,灯被开关短路,灯不亮;开关断开时,灯才亮。第二节 逻辑门真值表非门波形图第二节 逻辑门思考与、或、非分别和集合论中的哪些运算是互相对应的?
指出图中表示“A×B”,“A+B”,A,B,“A×B的非”的范围。与——交集
或——并集
非——补集案例分析 分析本节开始的三人表决器案例,输出与输入之间的逻辑关系应该怎样表达,可用哪些门电路实现。第二节 逻辑门 该表决器有3个输入端,用A、B、C分别代表甲、乙、丙投票人,它们各在投赞成票时为1,不投赞成票时为0;有2个输出端,用L1表示表决通过(绿色指示灯亮),L2表示表决不通过(红色指示灯亮)。
根据它们之间的逻辑关系,能使LI为1的情况有4种:甲、乙同意,乙、
丙同意,甲、丙同意和甲、乙、丙3人都同意。将这4种情况分别用l1、l2、l3和l4代表,
显然:
第二节 逻辑门三人表决器只有A、B同为1时才为1,所以l1=_A×B;
只有B、C同为1时才为1,所以l2=_____;
只有A、C同为1时才为1,所以l3=_____;
只有A、B、C同为1时才为1,所以l4=_____;
绿灯L1=_____
红灯L2=_____l1+l2+l3+l4=AB+BC+AC+ABC
B×CA×CA×B×C三人表决器&&&&&l1l3l2l4绿灯CBA红灯与逻辑三人表决器(精简)l1l3l2绿灯CBA红灯三种门电路的逻辑关系与门:“全高出高,有低出低”
或门:“见高出高,全低出低”
非门:“见高出低,见低出高”
第二节 逻辑门L4=ABC与非门和或非门 “与非”关系和“或非”关系是从三种基本逻辑关系推演出来的复合逻辑关系.实现这两种逻辑关系的门电路分别称为与非门(NAND)和或非门(NOR)。
与非门的真值表和与门的真值表中的输出逻辑值完全相反:与门的逻辑关系是“全高出高,有低出低”,而与非门的逻辑关系则是“全高出低,有低出高”,因此其逻辑关系相当于在与门后面再接一只非门。
与门逻辑关系是“全高出高,有低出低”与非门逻辑关系是“全高出低,有低出高” + =1、与非门与非门波形图
与非门的真值表和与门的真值表中的输出逻辑值完全相反;与门 F=A×B 与非门 F=A×B&
与非门“全高出低,有低出高”下图是一与非门的输入信号波形,请画出输出波形2、或非门或非门的真值表和或门的真值表相反或门: “见高出高,全低出低”或非门:“见高出低,全低出高”请填写此表马上行动或门输出信号或非门输出信号请画出下图中或非门输出信号三种门电路的逻辑关系与门:“全高出高,见低出低”
或门:“见高出高,全低出低”
非门:“见高出低,见低出高”
与非门:“全高出低,见低出高”
或非门:“见高出低,全低出高”
谢谢
电子控制系统的控制(处理)部分于是依据各输出信号与输入信号之间的逻辑关系(因果关系)来处理的。为处理方便,将逻辑前提和逻辑结论均用字母A、B、C等表示,显然,这些字母都应当只有“真”和“假”两个状态,且非真即假,非假即真。
实现各种逻辑关系的电路称为数字电路(或逻辑电路)。在数字电路中,“真”用高电平(“1”)表示,“假”用低电平(“0”)表示。“1”和“0”称为数字电路的真值或逻辑值。三种基本的逻辑门 任何复杂的逻辑关系都由“与”、“或”、“非”三种基本逻辑关系组合而成,实现这三种基本逻辑关系的电路分别称为与门(AND)、或门(OR)和非门(NOT),它们的输入信号代表逻辑前提,输出信号代表逻辑结论。思考 请列举在日常生活中常见的与逻辑有关系的例子 与逻辑关系举例:
1.火车在开动时,所有车门必须关好,如有车门没关不能放行。
2.我国婚姻法规定,男女双方必须同时到场方可登记结婚。
3.开学时班长宜布班级活动计划:三月份将选择一个晴朗的星期六去郊游。
4.小明家走廊上有一盏节能路灯,天黑以后,有人通过并发出响声时,灯才亮,其他情况下灯不亮。
5.仓库的门通常用两把锁,由不同的人保管,开门时必须两个保管人同时到场。与门“所有逻辑前提皆为真时,逻辑结论才为真”的逻辑关系称为“与”逻辑关系。(1)什么是与门?
——实现与逻辑关系的电路称为与门。1、与门 开关串联电路 两只开关控制一盏灯亮和灭的电路,在真值表内 填入灯亮与否的情况。 真值表 若令开关通为真,断为假;灯亮为真,不亮为假,请判断该电路是否为与逻辑关系。(2)与门电路的特点:
只有当与门的所有输入端皆为高电平“1”时,输出端才为高电平“1”。即“全高出高,有低出低” 特点:
“全高出高,有低出低”
(3)与逻辑关系在布尔代数中定义为逻辑乘法,记作:F=A*B F=A.B F=AB(4)与逻辑符号 数字电路的逻辑关系常常用波形图来描述,波形图记录门电路的输人信号或输出信号的电子随时间变化的情况,如右图所示。 右图小的与门在A和B两个波形的输入电压的作用下,得到如F波形所示的输出电压。第二节 逻辑门 在画波形图时,常常省去坐标轴,但输入波形与输出波形之间的时间必须严格对应,如下图中虚线所示。图中第三个时间区间,输入A和输入B都为1,符合“全高出高”规则,因而输出F也为1,其他情况不符合,因而输出为0。与门的输入、输出波形图“全高出高,有低出低”F马上行动“全高出高,有低出低”思 考“全高出高,有低出低” 或逻辑关系举例:
1.暑假里,高二(3)班同学一起到青岛去旅游。从上海到青岛可以乘火车、汽车,飞机,还可以乘海轮。
2 .高二(1)班教室有3把钥匙,班主任1把,班长1把,值日生1把,谁先到校都可以开门。
3.小明家楼顶的水箱通常在天黑以后进水,但若白天水箱的水用完了也能进水。
4.班主任通知开家长会时要求:父亲来可以,母亲来也可以,父母一起来更好。或门 “逻辑前提中有一个或一个以上为真,逻辑结论就为真”的逻辑关系称为“或”逻辑关系。例如,到图书馆借书,可以凭本校学生证也可以凭借书证,两证中有一个即可,这里的逻辑关系就是或逻辑关系。 请列举在日常生活中常见的或逻辑有关系的例子第二节 逻辑门ALB断通真值表断断断通通断通通通通马上行动两只开关控制一盏灯亮和灭的电路,在真值表内填入灯亮与否的情况。
(1)“逻辑前提中有一个或一个以上为真,逻辑结论就为真”
即:“见高出高,全低出低”
(2)或逻辑关系在布尔代数中定义为逻辑加法,记作: F=A+B
(3)实现或逻辑关系的电路称为或门。
(并联开关电路)2、或门(4)或逻辑关系符号马上行动 列出3个输入端的或门真值表,并画出输出波形“见高出高,全低出低” “逻辑前提为假时逻辑结论为真,逻辑前提为真时逻辑结论反而为假”,即逻辑结论与逻辑前提的逻辑值总是相反的逻辑关系称为非逻辑关系。记作:F = A读作“A非”。非逻辑关系的真值表如下表所示。从真值表可以看出:
0 = 1, 1 = 0 非门
F = A 非逻辑的例子如机场或车站旅客入口处要进行安全检查,带有易燃易爆物品者不得入内。第二节 逻辑门(1)“逻辑前提为假时逻辑结论为真,逻辑结论为真时逻辑结论反而为假”3、非门逻辑结论与逻辑前提的逻辑值总是相反.记作:(2)实现非逻辑关系的电路称为非门。(3)非门逻辑符号即:“见高出低,见低出高 ” 若以体温低于38℃为逻辑前提,则此逻辑前提与进单位办公和进观察室检查这两个逻辑结论之间,哪一个符合非逻辑关系?思考案例分析 “非典”流行时期,某单位的工作人员进单位办公均必须测体温,若体温超过38℃,则不能进入单位办公,且要进入观察室接受其他检查。这里,体温超过38℃ ,是逻辑前提,进单位办公和进观察室检查是两个逻辑结论,进单位办公与体温超过38℃之间是非逻辑关系,而进观察室检查与体温超过38℃之间则不是非逻辑关系。第二节 逻辑门ALR真值表马上行动 下图是描述非逻辑关系的示意图。请说明在上述案例中.应对逻辑前提A的逻辑结论L的真和假如何规定,才能符合非逻辑关系的定义?为什么? A:开关合上为真;
L:灯亮为真。
因为开关合上时,灯被开关短路,灯不亮;开关断开时,灯才亮。第二节 逻辑门真值表非门波形图第二节 逻辑门思考与、或、非分别和集合论中的哪些运算是互相对应的?
指出图中表示“A×B”,“A+B”,A,B,“A×B的非”的范围。与——交集
或——并集
非——补集案例分析 分析本节开始的三人表决器案例,输出与输入之间的逻辑关系应该怎样表达,可用哪些门电路实现。第二节 逻辑门 该表决器有3个输入端,用A、B、C分别代表甲、乙、丙投票人,它们各在投赞成票时为1,不投赞成票时为0;有2个输出端,用L1表示表决通过(绿色指示灯亮),L2表示表决不通过(红色指示灯亮)。
根据它们之间的逻辑关系,能使LI为1的情况有4种:甲、乙同意,乙、
丙同意,甲、丙同意和甲、乙、丙3人都同意。将这4种情况分别用l1、l2、l3和l4代表,
显然:
第二节 逻辑门三人表决器只有A、B同为1时才为1,所以l1=_A×B;
只有B、C同为1时才为1,所以l2=_____;
只有A、C同为1时才为1,所以l3=_____;
只有A、B、C同为1时才为1,所以l4=_____;
绿灯L1=_____
红灯L2=_____l1+l2+l3+l4=AB+BC+AC+ABC
B×CA×CA×B×C三人表决器&&&&&l1l3l2l4绿灯CBA红灯与逻辑三人表决器(精简)l1l3l2绿灯CBA红灯三种门电路的逻辑关系与门:“全高出高,有低出低”
或门:“见高出高,全低出低”
非门:“见高出低,见低出高”
第二节 逻辑门L4=ABC与非门和或非门 “与非”关系和“或非”关系是从三种基本逻辑关系推演出来的复合逻辑关系.实现这两种逻辑关系的门电路分别称为与非门(NAND)和或非门(NOR)。
与非门的真值表和与门的真值表中的输出逻辑值完全相反:与门的逻辑关系是“全高出高,有低出低”,而与非门的逻辑关系则是“全高出低,有低出高”,因此其逻辑关系相当于在与门后面再接一只非门。
与门逻辑关系是“全高出高,有低出低”与非门逻辑关系是“全高出低,有低出高” + =1、与非门与非门波形图
与非门的真值表和与门的真值表中的输出逻辑值完全相反;与门 F=A×B 与非门 F=A×B&
与非门“全高出低,有低出高”下图是一与非门的输入信号波形,请画出输出波形2、或非门或非门的真值表和或门的真值表相反或门: “见高出高,全低出低”或非门:“见高出低,全低出高”请填写此表马上行动或门输出信号或非门输出信号请画出下图中或非门输出信号三种门电路的逻辑关系与门:“全高出高,见低出低”
或门:“见高出高,全低出低”
非门:“见高出低,见低出高”
与非门:“全高出低,见低出高”
或非门:“见高出低,全低出高”
谢谢
同课章节目录
