1.3 简单曲线的极坐标方程 课件1
文档属性
| 名称 | 1.3 简单曲线的极坐标方程 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-19 15:54:43 | ||
图片预览










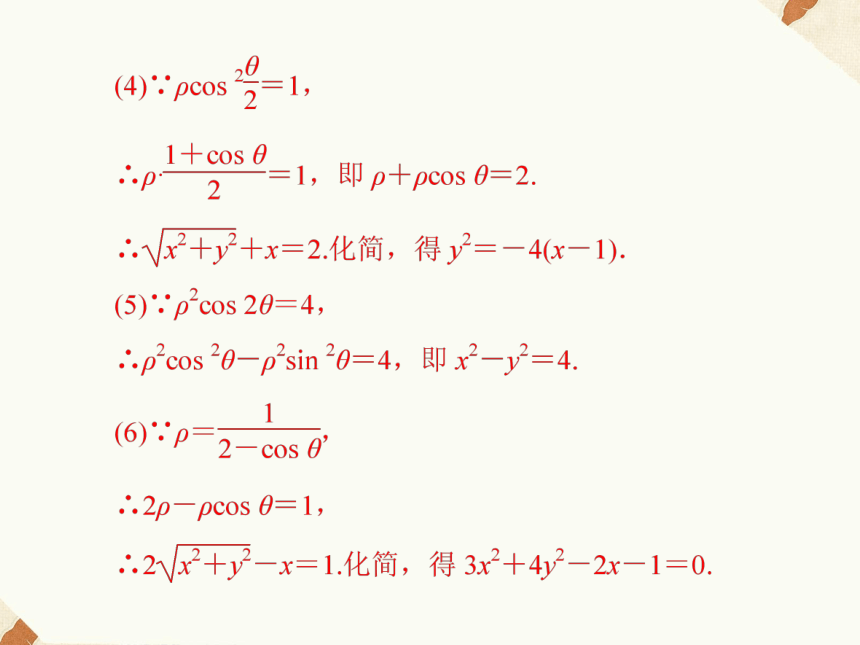
文档简介
课件30张PPT。三 简单曲线的极坐标方程1.理解极坐标方程的意义.
2.能在极坐标中给出简单图形的极坐标方程.
3.通过比较这些图形在极坐标系和平面直角坐标系中的方程,体会在用方程刻画平面图形时选择适当坐标系的意义.1.定义
如果曲线C上的点与方程f(ρ,θ)=0有如下关系:
(1)曲线C上任一点的坐标(所有坐标中至少有一个)符合方程f(ρ,θ)=0.
(2)方程f(ρ,θ)=0的所有解为坐标的点都在曲线C上,则曲线C的方程是f(ρ,θ)=0.
2.直线的极坐标方程
若直线过点M(ρ0,θ0),且极轴到此直线的角为α,则它的方程为ρsin (θ-α)=ρ0sin (θ0-α).3.圆的极坐标方程
圆心为M(ρ0,θ0)、半径为r的圆方程为
ρ2-2ρ0ρcos (θ-θ0)+ -r2=0.
特别当圆心与极点重合时,圆的方程为ρ=r.?练习几个特殊位置的直线的极坐标方程.
①直线过极点且过点M(ρ0,θ0)的极坐标方程为____________.
②直线过点M(a,0)且垂直于极轴的极坐标方程为____________.
③直线过点M 且平行于极轴的极坐标方程为____________.2.①θ=θ0 ②ρcosθ=a ③ρsinθ=b练习(1)几个特殊位置的圆的极坐标方程:
①当圆心位于极点、半径为r的圆的极坐标方程为_______.
②当圆心位于M(r,0)、半径为r的圆的极坐标方程为______.
③当圆心位于M 、半径为r的圆的极坐标方程为_________.
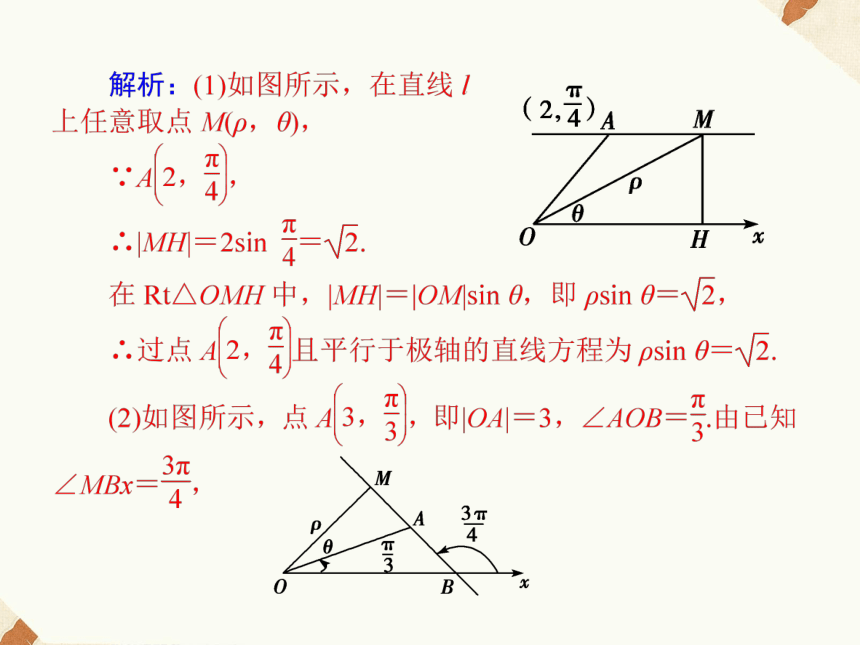
3.ρcos θ=3,ρ=5,ρsinθ=2,θ= π分别表示什么曲线?答案:ρcosθ=3,ρ=5,ρsinθ=2,θ= π(ρ>0)分别表示直线、圆、直线、射线. 求: (1)求过点A 且平行于极轴的直线.
(2)过A 且和极轴成 的直线.分析:(1)在直线上任意取一点M,根据已知条件想办法找到变量ρ,θ之间的关系.我们可以通过直角三角形来解决,因为已知OA的长度,还知∠AOx= .
(2)在三角形中,利用正弦定理来找到变量ρ,θ之间的关系.进行直角坐标方程与极坐标方程的互化. 分析:极坐标系和直角坐标系都是用一对有序实数来确定平面上一点的位置方法,都是研究平面图形的重要工具.在实践中,由于问题的需要和研究的方便,常需把这两种坐标系进行换算,我们有必要掌握这两种坐标间的互化.在解这类题时,除正确使用互化公式外,还要注意与恒等变换等知识相结合.1.极坐标方程分别为ρ=cos θ和ρ=sin θ的两个圆的圆心距是( )
A.2 B. C.1 D.D 2.极坐标方程ρ=cos 所表示的曲线是( )
A.双曲线 B.椭圆
C.抛物线 D.圆D C 解析:把圆的极坐标方程化为直角坐标系方程为x2+y2+2y=0,得圆心的直角坐标为(0,-1),故选B.
答案:B6.已知曲线C1,C2的极坐标方程分别为ρcos θ=3,ρ=4cos θ , 则曲线C1与C2交点的极坐标为________.7.才曲线C的直角坐标方程为x2+y2-2x=0?.以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为____________.解析:利用公式法转化求解.?
直角坐标方程x2+y2-2x=0 可以为x2+y2=2x,将ρ2=x2+y2,x=ρcosθ代入整理得:ρ=2cosθ.?
答案:ρ=2cosθ8.在极坐标系中,曲线C1:ρ( cos θ+sin θ)=1与曲线C2:ρ=a(a>0)的一个交点在极轴上,则a=________.9.直线2ρcos θ=1与圆ρ=2cos θ相交的弦长为________.10.把下列极坐标方程化为直角坐标方程.
(1)ρ2cos 2θ=1.
(2)ρ=tan θ·sec θ.
(3)ρ=2cos .分析:本题考查极坐标方程转化为直角坐标方程,通常把方程先配凑,然后把ρcos θ换成x,ρsin θ换成y,ρ2换成x2+y2而得出.11.设过原点O的直线与圆C:(x-1)2+y2=1的一个交点为P,点M为线段OP的中点.
(1)求圆C的极坐标方程;
(2)求点M轨迹的极坐标方程,并说明它是什么曲线.解析:(1)圆(x-1)2+y2=1的极坐标方程为ρ=2cos θ.
(2)设点P的极坐标为(ρ1,θ1),点M的极坐标为(ρ,θ).
∵点M为线段OP的中点,∴ρ1=2ρ,θ1=θ.
将ρ1=2ρ,θ1=θ代入圆的极坐标方程,得ρ=cos θ.
∴点M轨迹的极坐标方程为ρ=cos θ,它表示圆心在 点 ,半径为 的圆. 1.极坐标系和直角坐标系都可以建立点与数组、曲线
与方程之间的对应关系.并且在某些情况下,应用极坐标
系解题比应用直角坐标系更为简洁.所以必须掌握用极坐
标系解决问题的方法,熟悉极坐标系与直角坐标系的互相
转化关系.?
首先,我们应注意到极坐标系与直角坐标系存在着不
同点,这是因为极坐标系中点与数之间的对应关系不是一
一映射的.?
2.建立曲线的极坐标方程的方法步骤.?
(1)在曲线上任取一点P(ρ,θ).?
(2)建立起直角三角形(或斜三角形),利用锐角的三
角函数概念、正弦定理、余弦定理建立起ρ、θ的方程.?
(3)证明所求曲线方程为曲线的方程(在此省略).? 3.利用极坐标思想方法亦可简便解决一些轨迹问题,
尤其是涉及线段间数量关系的问题.求极坐标系下的轨迹
方程与求直角坐标系下的轨迹方程的方法一致.如定义
法、直接法、参数法等.?
4.不论曲线的直角坐标系的方程如何,只要我们将极
坐标系的极点放在曲线的焦点上,总可将方程化成较简单
的极坐标方程.反过来,有了适当的极坐标方程和直角坐
标系与极坐标系的位置关系,也可以得到曲线在直角坐标
系内的方程.这样,在解题过程中,我们就可以灵活地变换坐标系,使解题过程大为简化.?
5.处理极坐标系中的直线与圆的问题大致有两种思路:?
(1)化极坐标方程为直角坐标方程再处理;?
(2)根据ρ、θ的几何意义进行旋转或伸缩变换.本小节结束
2.能在极坐标中给出简单图形的极坐标方程.
3.通过比较这些图形在极坐标系和平面直角坐标系中的方程,体会在用方程刻画平面图形时选择适当坐标系的意义.1.定义
如果曲线C上的点与方程f(ρ,θ)=0有如下关系:
(1)曲线C上任一点的坐标(所有坐标中至少有一个)符合方程f(ρ,θ)=0.
(2)方程f(ρ,θ)=0的所有解为坐标的点都在曲线C上,则曲线C的方程是f(ρ,θ)=0.
2.直线的极坐标方程
若直线过点M(ρ0,θ0),且极轴到此直线的角为α,则它的方程为ρsin (θ-α)=ρ0sin (θ0-α).3.圆的极坐标方程
圆心为M(ρ0,θ0)、半径为r的圆方程为
ρ2-2ρ0ρcos (θ-θ0)+ -r2=0.
特别当圆心与极点重合时,圆的方程为ρ=r.?练习几个特殊位置的直线的极坐标方程.
①直线过极点且过点M(ρ0,θ0)的极坐标方程为____________.
②直线过点M(a,0)且垂直于极轴的极坐标方程为____________.
③直线过点M 且平行于极轴的极坐标方程为____________.2.①θ=θ0 ②ρcosθ=a ③ρsinθ=b练习(1)几个特殊位置的圆的极坐标方程:
①当圆心位于极点、半径为r的圆的极坐标方程为_______.
②当圆心位于M(r,0)、半径为r的圆的极坐标方程为______.
③当圆心位于M 、半径为r的圆的极坐标方程为_________.
3.ρcos θ=3,ρ=5,ρsinθ=2,θ= π分别表示什么曲线?答案:ρcosθ=3,ρ=5,ρsinθ=2,θ= π(ρ>0)分别表示直线、圆、直线、射线. 求: (1)求过点A 且平行于极轴的直线.
(2)过A 且和极轴成 的直线.分析:(1)在直线上任意取一点M,根据已知条件想办法找到变量ρ,θ之间的关系.我们可以通过直角三角形来解决,因为已知OA的长度,还知∠AOx= .
(2)在三角形中,利用正弦定理来找到变量ρ,θ之间的关系.进行直角坐标方程与极坐标方程的互化. 分析:极坐标系和直角坐标系都是用一对有序实数来确定平面上一点的位置方法,都是研究平面图形的重要工具.在实践中,由于问题的需要和研究的方便,常需把这两种坐标系进行换算,我们有必要掌握这两种坐标间的互化.在解这类题时,除正确使用互化公式外,还要注意与恒等变换等知识相结合.1.极坐标方程分别为ρ=cos θ和ρ=sin θ的两个圆的圆心距是( )
A.2 B. C.1 D.D 2.极坐标方程ρ=cos 所表示的曲线是( )
A.双曲线 B.椭圆
C.抛物线 D.圆D C 解析:把圆的极坐标方程化为直角坐标系方程为x2+y2+2y=0,得圆心的直角坐标为(0,-1),故选B.
答案:B6.已知曲线C1,C2的极坐标方程分别为ρcos θ=3,ρ=4cos θ , 则曲线C1与C2交点的极坐标为________.7.才曲线C的直角坐标方程为x2+y2-2x=0?.以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为____________.解析:利用公式法转化求解.?
直角坐标方程x2+y2-2x=0 可以为x2+y2=2x,将ρ2=x2+y2,x=ρcosθ代入整理得:ρ=2cosθ.?
答案:ρ=2cosθ8.在极坐标系中,曲线C1:ρ( cos θ+sin θ)=1与曲线C2:ρ=a(a>0)的一个交点在极轴上,则a=________.9.直线2ρcos θ=1与圆ρ=2cos θ相交的弦长为________.10.把下列极坐标方程化为直角坐标方程.
(1)ρ2cos 2θ=1.
(2)ρ=tan θ·sec θ.
(3)ρ=2cos .分析:本题考查极坐标方程转化为直角坐标方程,通常把方程先配凑,然后把ρcos θ换成x,ρsin θ换成y,ρ2换成x2+y2而得出.11.设过原点O的直线与圆C:(x-1)2+y2=1的一个交点为P,点M为线段OP的中点.
(1)求圆C的极坐标方程;
(2)求点M轨迹的极坐标方程,并说明它是什么曲线.解析:(1)圆(x-1)2+y2=1的极坐标方程为ρ=2cos θ.
(2)设点P的极坐标为(ρ1,θ1),点M的极坐标为(ρ,θ).
∵点M为线段OP的中点,∴ρ1=2ρ,θ1=θ.
将ρ1=2ρ,θ1=θ代入圆的极坐标方程,得ρ=cos θ.
∴点M轨迹的极坐标方程为ρ=cos θ,它表示圆心在 点 ,半径为 的圆. 1.极坐标系和直角坐标系都可以建立点与数组、曲线
与方程之间的对应关系.并且在某些情况下,应用极坐标
系解题比应用直角坐标系更为简洁.所以必须掌握用极坐
标系解决问题的方法,熟悉极坐标系与直角坐标系的互相
转化关系.?
首先,我们应注意到极坐标系与直角坐标系存在着不
同点,这是因为极坐标系中点与数之间的对应关系不是一
一映射的.?
2.建立曲线的极坐标方程的方法步骤.?
(1)在曲线上任取一点P(ρ,θ).?
(2)建立起直角三角形(或斜三角形),利用锐角的三
角函数概念、正弦定理、余弦定理建立起ρ、θ的方程.?
(3)证明所求曲线方程为曲线的方程(在此省略).? 3.利用极坐标思想方法亦可简便解决一些轨迹问题,
尤其是涉及线段间数量关系的问题.求极坐标系下的轨迹
方程与求直角坐标系下的轨迹方程的方法一致.如定义
法、直接法、参数法等.?
4.不论曲线的直角坐标系的方程如何,只要我们将极
坐标系的极点放在曲线的焦点上,总可将方程化成较简单
的极坐标方程.反过来,有了适当的极坐标方程和直角坐
标系与极坐标系的位置关系,也可以得到曲线在直角坐标
系内的方程.这样,在解题过程中,我们就可以灵活地变换坐标系,使解题过程大为简化.?
5.处理极坐标系中的直线与圆的问题大致有两种思路:?
(1)化极坐标方程为直角坐标方程再处理;?
(2)根据ρ、θ的几何意义进行旋转或伸缩变换.本小节结束
