2.2 圆锥曲线的参数方程 课件1
文档属性
| 名称 | 2.2 圆锥曲线的参数方程 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 566.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-19 16:13:33 | ||
图片预览



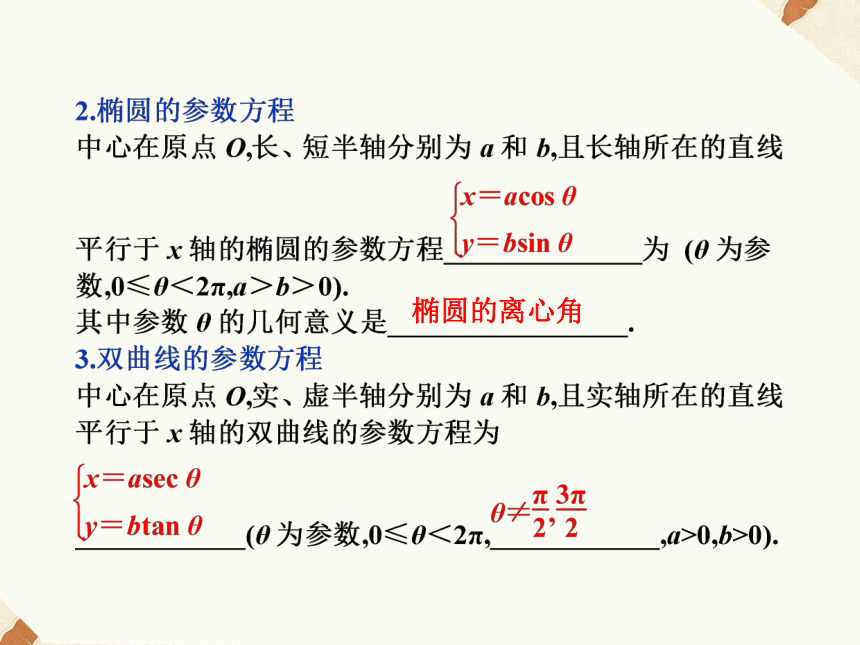





文档简介
课件23张PPT。2.2 圆锥曲线的参数方程学习目标
1.分析圆锥曲线的几何性质,选择适当的参数写出它们的参数方程.
2.应用圆锥曲线的参数方程解决具体的问题.旋转角椭圆的离心角题型一 椭圆参数方程的应用【名师点评】 参数方程的主要价值在于坐标一元化及三角技巧的运用.本例运用了椭圆的参数方程,将一个二元条件极值问题,转化为一个一元三角极值的计算,同时由于设参数而创造了运用三角技巧的条件,从而达到了简化运算的目的.变式训练
1.在椭圆4x2+9y2=36上求一点P,使以P,A(-2,-8),B(-6,-6)为顶点的三角形面积最小.题型二 双曲线参数方程的应用 求证:双曲线上任一点到两渐近线的距离的乘积是一个定值.【名师点评】 在研究最值和定值问题中,使用曲线的参数方程非常简捷方便,点到直线的距离公式对参数形式的点的坐标仍适用,注意公式sec2φ-tan2φ=1的应用.变式训练
2.如图,设P为等轴双曲线x2-y2=1上的一点,F1、F2是两个焦点,求证:|PF1|·|PF2|=|OP|2.
题型三 抛物线参数方程的应用 过抛物线y2=2px(p>0)的顶点作互相垂直的两弦OA、OB.
(1)求线段AB中点M的轨迹方程;
(2)分别以弦OA、OB为直径画圆,求两圆另一交点H的轨迹.【名师点评】 此例是用参数法求多动点轨迹的典型题.题(1)中求得x=f(t1,t2),y=g(t1,t2)后,要注意重审题意,发现t1·t2=-1这个关键式子.题(2)是变换视角求两动直线交点的轨迹,也可先求出以OA、OB为直径的圆的方程,再通过方程相减等变形消参求解.变式训练
3.过抛物线y2=2px(p>0)的顶点O作两条互相垂直的弦OA、OB.
(1)设OA的斜率为k,试用k表示点A、B的坐标;
(2)求弦AB中点M的轨迹方程.(用不同于例3的方法求解)题型四 应用参数求曲线的轨迹方程 设抛物线y2=2px(p>0)的准线为l,焦点为F,顶点为O,P为抛物线上任一点,PQ⊥l于Q,求QF与OP的交点M的轨迹方程.【名师点评】 用参数法求动点的轨迹方程,其基本思想是选取适当的参数作为中间变量,使动点的坐标分别与参数有关,从而得到动点的参数方程,然后再消去参数,化为普通方程,如果动点轨迹与圆锥曲线有关,通常以圆锥曲线的参数方程中的参数作为中间变量.变式训练
4.△ABC一边AB固定,顶点C在一条平行于AB的定直线l上移动,设△ABC的垂心在三角形内,求垂心的轨迹方程.1.与圆锥曲线上的动点有联系的最值和定值问题,运用参数方程往往可以化难为易.
2.设参数求曲线的轨迹方程,主要有以下五步:
(1)建立坐标系;
(2)选参:常用的物理参数有时间、路程、速度等.几何参数有角θ,斜率k,线参数t等;
(3)用参:求动点的两个坐标与参数的关系式;
(4)消参;
(5)考查曲线纯粹性与完备性.
1.分析圆锥曲线的几何性质,选择适当的参数写出它们的参数方程.
2.应用圆锥曲线的参数方程解决具体的问题.旋转角椭圆的离心角题型一 椭圆参数方程的应用【名师点评】 参数方程的主要价值在于坐标一元化及三角技巧的运用.本例运用了椭圆的参数方程,将一个二元条件极值问题,转化为一个一元三角极值的计算,同时由于设参数而创造了运用三角技巧的条件,从而达到了简化运算的目的.变式训练
1.在椭圆4x2+9y2=36上求一点P,使以P,A(-2,-8),B(-6,-6)为顶点的三角形面积最小.题型二 双曲线参数方程的应用 求证:双曲线上任一点到两渐近线的距离的乘积是一个定值.【名师点评】 在研究最值和定值问题中,使用曲线的参数方程非常简捷方便,点到直线的距离公式对参数形式的点的坐标仍适用,注意公式sec2φ-tan2φ=1的应用.变式训练
2.如图,设P为等轴双曲线x2-y2=1上的一点,F1、F2是两个焦点,求证:|PF1|·|PF2|=|OP|2.
题型三 抛物线参数方程的应用 过抛物线y2=2px(p>0)的顶点作互相垂直的两弦OA、OB.
(1)求线段AB中点M的轨迹方程;
(2)分别以弦OA、OB为直径画圆,求两圆另一交点H的轨迹.【名师点评】 此例是用参数法求多动点轨迹的典型题.题(1)中求得x=f(t1,t2),y=g(t1,t2)后,要注意重审题意,发现t1·t2=-1这个关键式子.题(2)是变换视角求两动直线交点的轨迹,也可先求出以OA、OB为直径的圆的方程,再通过方程相减等变形消参求解.变式训练
3.过抛物线y2=2px(p>0)的顶点O作两条互相垂直的弦OA、OB.
(1)设OA的斜率为k,试用k表示点A、B的坐标;
(2)求弦AB中点M的轨迹方程.(用不同于例3的方法求解)题型四 应用参数求曲线的轨迹方程 设抛物线y2=2px(p>0)的准线为l,焦点为F,顶点为O,P为抛物线上任一点,PQ⊥l于Q,求QF与OP的交点M的轨迹方程.【名师点评】 用参数法求动点的轨迹方程,其基本思想是选取适当的参数作为中间变量,使动点的坐标分别与参数有关,从而得到动点的参数方程,然后再消去参数,化为普通方程,如果动点轨迹与圆锥曲线有关,通常以圆锥曲线的参数方程中的参数作为中间变量.变式训练
4.△ABC一边AB固定,顶点C在一条平行于AB的定直线l上移动,设△ABC的垂心在三角形内,求垂心的轨迹方程.1.与圆锥曲线上的动点有联系的最值和定值问题,运用参数方程往往可以化难为易.
2.设参数求曲线的轨迹方程,主要有以下五步:
(1)建立坐标系;
(2)选参:常用的物理参数有时间、路程、速度等.几何参数有角θ,斜率k,线参数t等;
(3)用参:求动点的两个坐标与参数的关系式;
(4)消参;
(5)考查曲线纯粹性与完备性.
