2.4 渐开线与摆线 课件2
图片预览








文档简介
课件23张PPT。四 渐开线与摆线 1.了解圆的渐开线的参数方程,了解摆线的生成过程及它的参数方程.
2.学习用向量知识推导运动轨迹曲线的方法和步骤. 给出圆的渐开线的参数方程
( 为参数),根据参数方程可以看
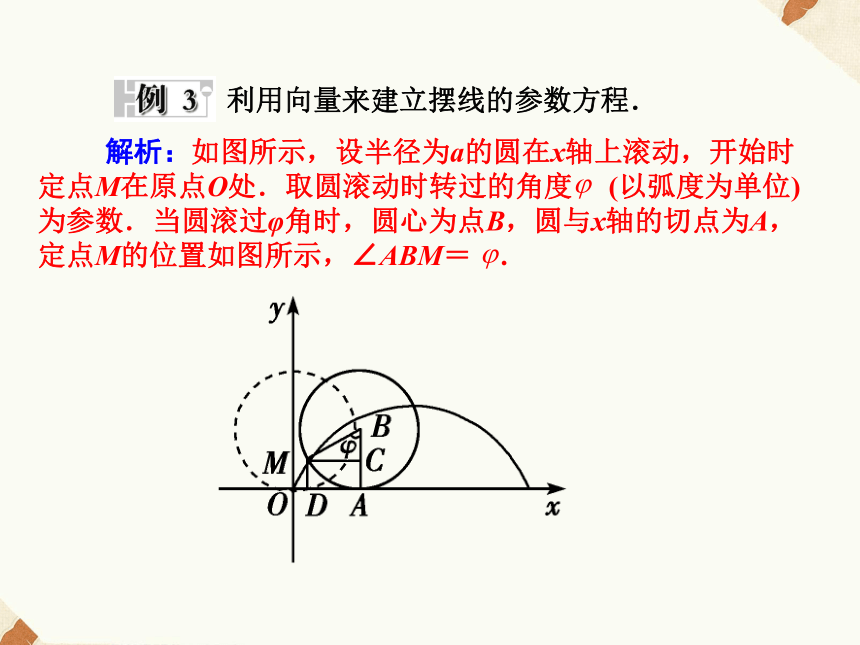
出,该渐开线的基圆半径是________,当参数 取 时,对应的曲线上的点的坐标是________. 按照给出的渐开线的直观定义,用初等方法推导圆的渐开线的参数方程. 利用向量来建立摆线的参数方程.
解析:如图所示,设半径为a的圆在x轴上滚动,开始时定点M在原点O处.取圆滚动时转过的角度 (以弧度为单位)为参数.当圆滚过φ角时,圆心为点B,圆与x轴的切点为A,定点M的位置如图所示,∠ABM= .1.下列关于渐开线和摆线的叙述中,正确的是( )
A.只有圆才有渐开线
B.渐开线和摆线的定义是一样的,只是绘图的方法不一样,所以才能得到不同的图形
C.正方形也可以有渐开线
D.对于同一个圆,如果建立的直角坐标系的位置不同,画出的渐开线形状就不同C 2.给出下列说法:①圆的渐开线的参数方程不能转化为普通方程;②圆的渐开线也可以转化为普通方程,但是转化后的普通方程比较麻烦,且不容易看出坐标之间的关系,所以常使用参数方程研究圆的渐开线问题;③在求圆的摆线和渐开线方程时,如果建立的坐标系原点和坐标轴选取不同,可能会得到不同的参数方程;④圆的渐开线和x轴一定有交点而且是唯一的交点.其中正确的说法有( )
A.①③ B.②④
C.②③ D.①③④C C 6.如图所示,ABCD是边长为1的正方形,曲线AEFGH…叫做“正方形的渐开线”,其中AE,EF,FG,GH…的圆心依次按B,C,D,A循环,它们依次相连接,则曲线AEFGH长是( )
A.3π
B.4π
C.5π
D.6πC 分析:首先根据所给的摆线方程,判断出圆的半径为4,易得圆的面积,再代入渐开线的参数方程的标准形式,即可得圆的渐开线的参数方程.分析:首先根据条件可知,圆的半径是6,平移后的圆心为O(0,0),根据圆心O到直线的距离,可以判断出直线和圆的位置关系.再由圆的半径写出圆的摆线方程.求摆线和x轴的交点只需令y=0,求出对应的参数 ,再代入求出x值.12.已知一个圆的摆线过一定点(2,0),请写出该圆的半径最大时该摆线的参数方程以及对应的圆的渐开线的参数方程.1.渐开线的实质是直线在圆上滚动时直线上定点的轨迹.圆的摆线的实质是一个圆沿着一条定直线无滑动地滚动时圆周上一个定点的轨迹.
2.渐开线上任一点M的坐标由圆心角 (以弧度为单位)唯一确定,而在圆的摆线中,圆周上定点M的位置也可以由圆心角 唯一确定.
3.圆的渐开线和摆线的参数方程均不宜化为普通方程,既烦琐又没有实际意义.
4.分析上面建立曲线的参数方程的过程,总结用向量方法建立运动轨迹的参数方程的基本思路和步骤.
它们的推导过程类似:
(1)建立合适的坐标系;
(2)取定某个角度(以弧度为单位)为参数;
(3)用三角知识写出相关向量的坐标表达式;
(4)用向量运算得到 的坐标表达式,就得到了曲线的参数方程.本小节结束
2.学习用向量知识推导运动轨迹曲线的方法和步骤. 给出圆的渐开线的参数方程
( 为参数),根据参数方程可以看
出,该渐开线的基圆半径是________,当参数 取 时,对应的曲线上的点的坐标是________. 按照给出的渐开线的直观定义,用初等方法推导圆的渐开线的参数方程. 利用向量来建立摆线的参数方程.
解析:如图所示,设半径为a的圆在x轴上滚动,开始时定点M在原点O处.取圆滚动时转过的角度 (以弧度为单位)为参数.当圆滚过φ角时,圆心为点B,圆与x轴的切点为A,定点M的位置如图所示,∠ABM= .1.下列关于渐开线和摆线的叙述中,正确的是( )
A.只有圆才有渐开线
B.渐开线和摆线的定义是一样的,只是绘图的方法不一样,所以才能得到不同的图形
C.正方形也可以有渐开线
D.对于同一个圆,如果建立的直角坐标系的位置不同,画出的渐开线形状就不同C 2.给出下列说法:①圆的渐开线的参数方程不能转化为普通方程;②圆的渐开线也可以转化为普通方程,但是转化后的普通方程比较麻烦,且不容易看出坐标之间的关系,所以常使用参数方程研究圆的渐开线问题;③在求圆的摆线和渐开线方程时,如果建立的坐标系原点和坐标轴选取不同,可能会得到不同的参数方程;④圆的渐开线和x轴一定有交点而且是唯一的交点.其中正确的说法有( )
A.①③ B.②④
C.②③ D.①③④C C 6.如图所示,ABCD是边长为1的正方形,曲线AEFGH…叫做“正方形的渐开线”,其中AE,EF,FG,GH…的圆心依次按B,C,D,A循环,它们依次相连接,则曲线AEFGH长是( )
A.3π
B.4π
C.5π
D.6πC 分析:首先根据所给的摆线方程,判断出圆的半径为4,易得圆的面积,再代入渐开线的参数方程的标准形式,即可得圆的渐开线的参数方程.分析:首先根据条件可知,圆的半径是6,平移后的圆心为O(0,0),根据圆心O到直线的距离,可以判断出直线和圆的位置关系.再由圆的半径写出圆的摆线方程.求摆线和x轴的交点只需令y=0,求出对应的参数 ,再代入求出x值.12.已知一个圆的摆线过一定点(2,0),请写出该圆的半径最大时该摆线的参数方程以及对应的圆的渐开线的参数方程.1.渐开线的实质是直线在圆上滚动时直线上定点的轨迹.圆的摆线的实质是一个圆沿着一条定直线无滑动地滚动时圆周上一个定点的轨迹.
2.渐开线上任一点M的坐标由圆心角 (以弧度为单位)唯一确定,而在圆的摆线中,圆周上定点M的位置也可以由圆心角 唯一确定.
3.圆的渐开线和摆线的参数方程均不宜化为普通方程,既烦琐又没有实际意义.
4.分析上面建立曲线的参数方程的过程,总结用向量方法建立运动轨迹的参数方程的基本思路和步骤.
它们的推导过程类似:
(1)建立合适的坐标系;
(2)取定某个角度(以弧度为单位)为参数;
(3)用三角知识写出相关向量的坐标表达式;
(4)用向量运算得到 的坐标表达式,就得到了曲线的参数方程.本小节结束
