1.3 圆锥曲线统一的极坐标方程 教案
文档属性
| 名称 | 1.3 圆锥曲线统一的极坐标方程 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 130.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-19 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.3
圆锥曲线统一的极坐标方程
教案
一、教学目的:
知识目标:进一步学习在极坐标系求曲线方程
能力目标:求出并掌握圆锥曲线的极坐标方程
德育目标:通过观察、探索、发现的创造性过程,培养创新意识.
二、重难点:
教学重点:圆锥曲线极坐标方程的统一形式
教学难点:方程中字母的几何意义
三、教学方法:
启发、诱导发现教学.
四、教学过程:
(一)、复习引入:
1、问题情境
情境1:直线与圆在极坐标系下都有确定的方程,我们熟悉的圆锥曲线呢?
情境2:按通常情况化直角坐标方程为极坐标方程会得到让人满意的结果吗?
2、学生回顾
(1).求曲线方程的方程的步骤
(2).两种坐标互化前提和公式
(3).圆锥曲线统一定义
(二)、讲解新课:
1、由必修课的学习我们已经知道:与一个定点的距离和一条定直线(定点不在定直线上)的距离的比等于常数e的点的轨迹,当e=1时,是抛物线.那么当01时,点的轨迹是什么曲线呢?可以借助极坐标系进行讨论.21cnjy.com
2、圆锥曲线的统一方程
设定点的距离为,求到定点到定点和定直线的距离之比为常数的点的轨迹的极坐标方程.分析:
①建系
②设点
③列出等式
④用极坐标、表示上述等式,并化简得极坐标方程
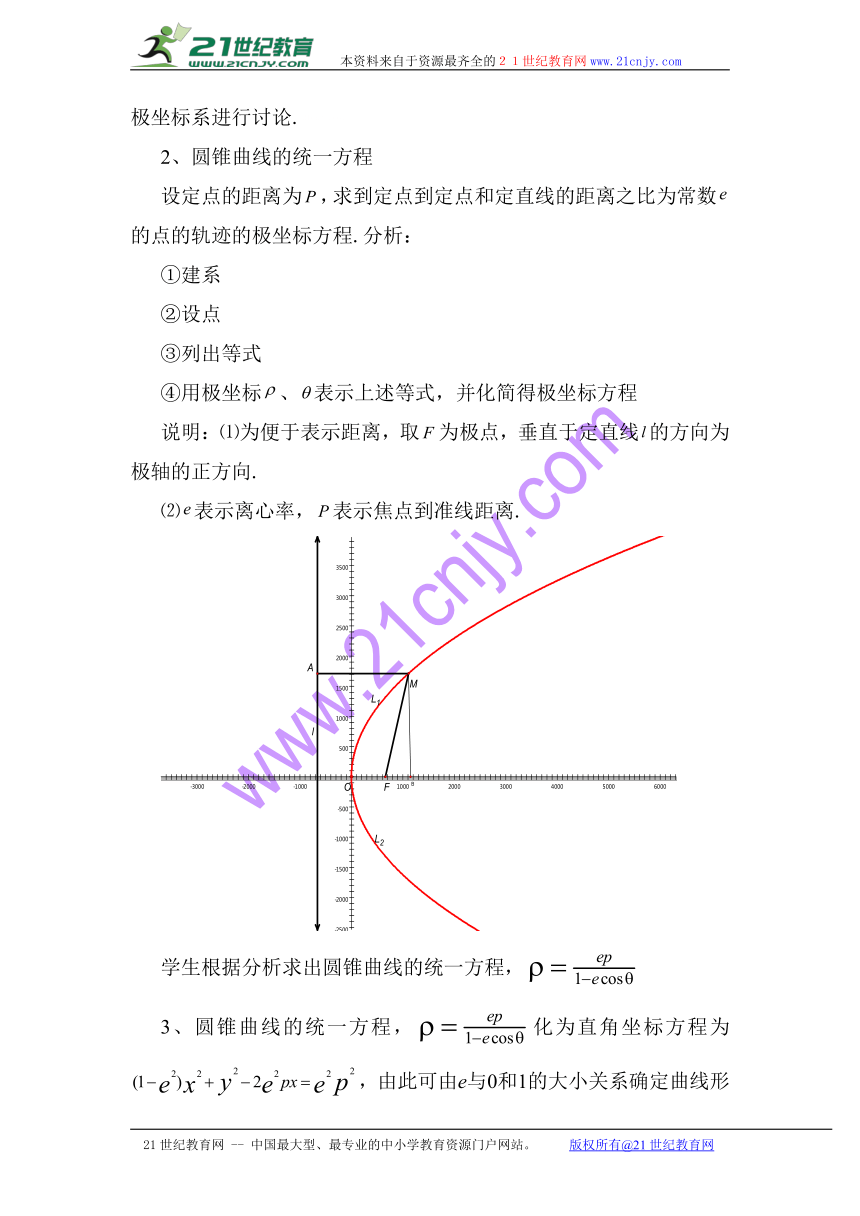
说明:⑴为便于表示距离,取为极点,垂直于定直线的方向为极轴的正方向.
⑵表示离心率,表示焦点到准线距离.
学生根据分析求出圆锥曲线的统一方程,
3、圆锥曲线的统一方程,化为直角坐标方程为,由此可由e与0和1的大小关系确定曲线形状.
4、思考交流:学生讨论交流课本P18页的问题:当01时,方程(1)表示了什么曲线?角在什么范围内变化即可得到曲线上所有的点?21教育网
2、例题讲解
例题:2003年10月15—17日,我国自主研制的神舟五号载人航天飞船成功发射并按预定方案安全、准确的返回地球,它的运行轨道先是以地球中心为一个焦点的椭圆,椭圆的近地点(离地面最近的点)和远地点(离地面最远的点)距离地面分别为200km和350km,然后进入距地面约343km的圆形轨道.若地球半径取6378km,试写出神舟五号航天飞船运行的椭圆轨道的极坐标方程.21·cn·jy·com
变式训练
已知抛物线的焦点为.
(1)以为极点,轴正方向为极轴的正方向,写出此抛物线的极坐标方程;
(2)过取作直线交抛物线于A、B两点,若|AB|=16,运用抛物线的极坐标方程,求直线的倾斜角.21世纪教育网版权所有
(三)、巩固练习:从极点O作圆C: =8cos的弦ON,求ON的中点M的轨迹方程.
答案: =4cos
(四)、小结:本课学习了以下内容:1、我们推导了圆锥曲线统一的极坐标方程,体会和掌握了求曲线的极坐标方程的方法步骤.2、把圆锥曲线统一的极坐标方程化为了直角坐标方程,从而判断了曲线形状,强化了互化公式的应用.
3、进一步理解和掌握了圆锥曲线统一的定义.www.21-cn-jy.com
(五)、作业:课本P19页A组中8、9、10
B组中2
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
1.3
圆锥曲线统一的极坐标方程
教案
一、教学目的:
知识目标:进一步学习在极坐标系求曲线方程
能力目标:求出并掌握圆锥曲线的极坐标方程
德育目标:通过观察、探索、发现的创造性过程,培养创新意识.
二、重难点:
教学重点:圆锥曲线极坐标方程的统一形式
教学难点:方程中字母的几何意义
三、教学方法:
启发、诱导发现教学.
四、教学过程:
(一)、复习引入:
1、问题情境
情境1:直线与圆在极坐标系下都有确定的方程,我们熟悉的圆锥曲线呢?
情境2:按通常情况化直角坐标方程为极坐标方程会得到让人满意的结果吗?
2、学生回顾
(1).求曲线方程的方程的步骤
(2).两种坐标互化前提和公式
(3).圆锥曲线统一定义
(二)、讲解新课:
1、由必修课的学习我们已经知道:与一个定点的距离和一条定直线(定点不在定直线上)的距离的比等于常数e的点的轨迹,当e=1时,是抛物线.那么当0
2、圆锥曲线的统一方程
设定点的距离为,求到定点到定点和定直线的距离之比为常数的点的轨迹的极坐标方程.分析:
①建系
②设点
③列出等式
④用极坐标、表示上述等式,并化简得极坐标方程
说明:⑴为便于表示距离,取为极点,垂直于定直线的方向为极轴的正方向.
⑵表示离心率,表示焦点到准线距离.
学生根据分析求出圆锥曲线的统一方程,
3、圆锥曲线的统一方程,化为直角坐标方程为,由此可由e与0和1的大小关系确定曲线形状.
4、思考交流:学生讨论交流课本P18页的问题:当0
2、例题讲解
例题:2003年10月15—17日,我国自主研制的神舟五号载人航天飞船成功发射并按预定方案安全、准确的返回地球,它的运行轨道先是以地球中心为一个焦点的椭圆,椭圆的近地点(离地面最近的点)和远地点(离地面最远的点)距离地面分别为200km和350km,然后进入距地面约343km的圆形轨道.若地球半径取6378km,试写出神舟五号航天飞船运行的椭圆轨道的极坐标方程.21·cn·jy·com
变式训练
已知抛物线的焦点为.
(1)以为极点,轴正方向为极轴的正方向,写出此抛物线的极坐标方程;
(2)过取作直线交抛物线于A、B两点,若|AB|=16,运用抛物线的极坐标方程,求直线的倾斜角.21世纪教育网版权所有
(三)、巩固练习:从极点O作圆C: =8cos的弦ON,求ON的中点M的轨迹方程.
答案: =4cos
(四)、小结:本课学习了以下内容:1、我们推导了圆锥曲线统一的极坐标方程,体会和掌握了求曲线的极坐标方程的方法步骤.2、把圆锥曲线统一的极坐标方程化为了直角坐标方程,从而判断了曲线形状,强化了互化公式的应用.
3、进一步理解和掌握了圆锥曲线统一的定义.www.21-cn-jy.com
(五)、作业:课本P19页A组中8、9、10
B组中2
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
