2.2.3 抛物线的参数方程 同步练习(无答案)
文档属性
| 名称 | 2.2.3 抛物线的参数方程 同步练习(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 158.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-19 00:00:00 | ||
图片预览

文档简介
2.2.3
抛物线的参数方程
同步练习
1.圆锥曲线(t为参数)的焦点坐标是________.
2.点P(1,0)到曲线(t为参数,t∈R)上的点的最短距离为(
)
A.0
B.1
C.
D.2
3.若曲线(t为参数)上异于原点的不同两点M1、M2所对应的参数分别是t1、t2,则弦M1M2所在直线的斜率是(
)
A.t1+t2
B.t1-t2
C.
D.
4.在平面直角坐标系中,已知直线l与曲线C的参数方程分别为l:(s为参数)和C(t为参数),若l与C相交于A、B两点,则|AB|=________.
5.连接原点O和抛物线x2=2y上的动点M,延长OM到点P,使|OM|=|MP|,求点P的轨迹方程,并说明它是何种曲线.
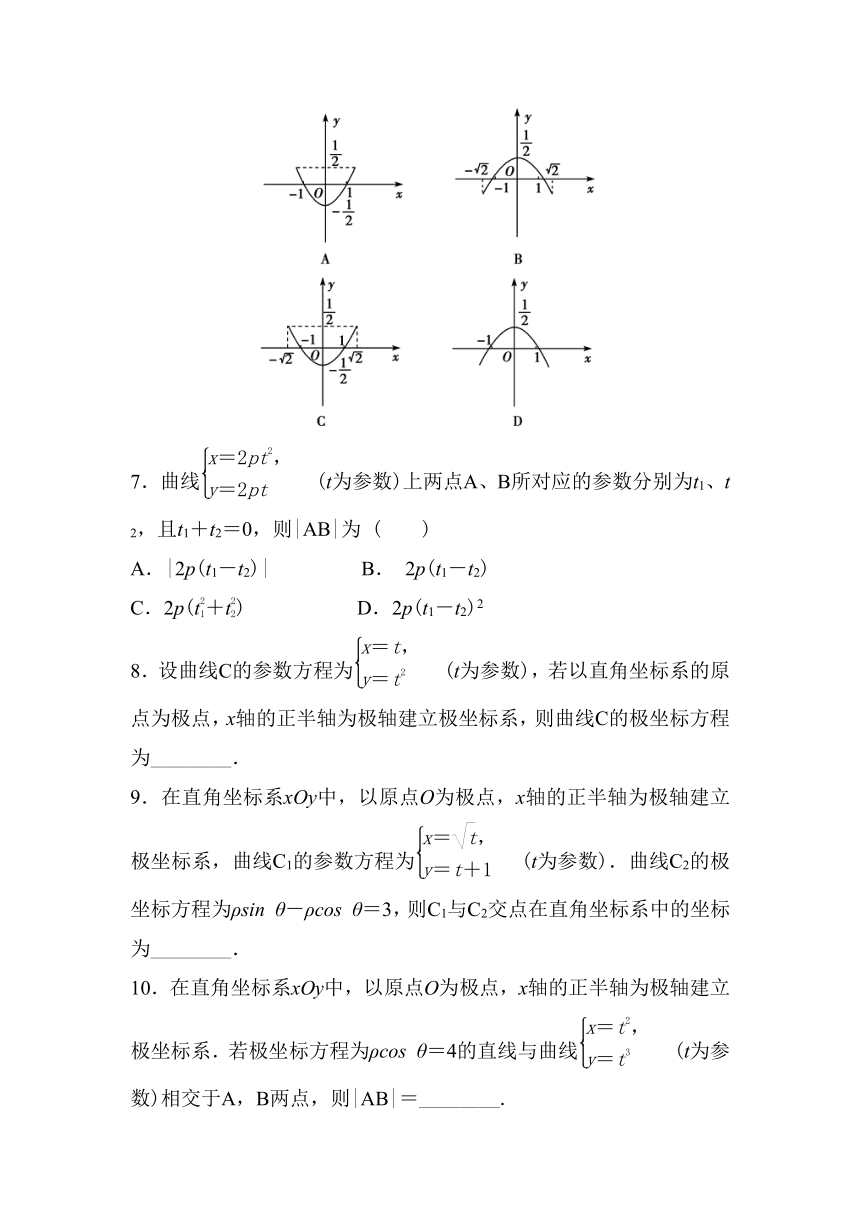
6.参数方程(θ为参数)表示的曲线为(
)
7.曲线(t为参数)上两点A、B所对应的参数分别为t1、t2,且t1+t2=0,则|AB|为
(
)
A.|2p(t1-t2)|
B.
2p(t1-t2)
C.2p(t+t)
D.2p(t1-t2)2
8.设曲线C的参数方程为(t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为________.
9.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的参数方程为(t为参数).曲线C2的极坐标方程为ρsin
θ-ρcos
θ=3,则C1与C2交点在直角坐标系中的坐标为________.
10.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若极坐标方程为ρcos
θ=4的直线与曲线(t为参数)相交于A,B两点,则|AB|=________.
11.在平面直角坐标系xOy中,直线l的参数方程为(t为参数),曲线C的参数方程为(θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.
12.已知抛物线y2=2px(p>0)过顶点的两弦OA⊥OB,求分别以OA、OB为直径的两圆的另一交点Q的轨迹.
13.过抛物线y2=2px(p>0)的顶点作两条互相垂直的弦OA、OB(如下图).
(1)设OA的斜率为k,试用k表示点A、B的坐标;
(2)求弦AB中点M的轨迹过程.
14.已知方程y2-2x-6ysin
θ-9cos2θ+8cos
θ+9=0.
(1)证明:不论θ为何值,该抛物线顶点的轨迹方程一定为椭圆;
(2)求抛物线在直线x=14上截得的弦长的取值范围,并求弦取得最值时相应的θ值.
抛物线的参数方程
同步练习
1.圆锥曲线(t为参数)的焦点坐标是________.
2.点P(1,0)到曲线(t为参数,t∈R)上的点的最短距离为(
)
A.0
B.1
C.
D.2
3.若曲线(t为参数)上异于原点的不同两点M1、M2所对应的参数分别是t1、t2,则弦M1M2所在直线的斜率是(
)
A.t1+t2
B.t1-t2
C.
D.
4.在平面直角坐标系中,已知直线l与曲线C的参数方程分别为l:(s为参数)和C(t为参数),若l与C相交于A、B两点,则|AB|=________.
5.连接原点O和抛物线x2=2y上的动点M,延长OM到点P,使|OM|=|MP|,求点P的轨迹方程,并说明它是何种曲线.
6.参数方程(θ为参数)表示的曲线为(
)
7.曲线(t为参数)上两点A、B所对应的参数分别为t1、t2,且t1+t2=0,则|AB|为
(
)
A.|2p(t1-t2)|
B.
2p(t1-t2)
C.2p(t+t)
D.2p(t1-t2)2
8.设曲线C的参数方程为(t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为________.
9.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的参数方程为(t为参数).曲线C2的极坐标方程为ρsin
θ-ρcos
θ=3,则C1与C2交点在直角坐标系中的坐标为________.
10.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若极坐标方程为ρcos
θ=4的直线与曲线(t为参数)相交于A,B两点,则|AB|=________.
11.在平面直角坐标系xOy中,直线l的参数方程为(t为参数),曲线C的参数方程为(θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.
12.已知抛物线y2=2px(p>0)过顶点的两弦OA⊥OB,求分别以OA、OB为直径的两圆的另一交点Q的轨迹.
13.过抛物线y2=2px(p>0)的顶点作两条互相垂直的弦OA、OB(如下图).
(1)设OA的斜率为k,试用k表示点A、B的坐标;
(2)求弦AB中点M的轨迹过程.
14.已知方程y2-2x-6ysin
θ-9cos2θ+8cos
θ+9=0.
(1)证明:不论θ为何值,该抛物线顶点的轨迹方程一定为椭圆;
(2)求抛物线在直线x=14上截得的弦长的取值范围,并求弦取得最值时相应的θ值.
