24.1.2 中心对称课件
图片预览





文档简介
课件14张PPT。24.1.2 中心对称(一)创设教学情景问题:你能举出几个实例或实物,说明它们也具有上面所说的特性吗? 教学目标:1、知识目标:学生理解掌握中心对称的概念及性质;
2、能力目标:经过探讨学习能熟练应用中心对称知识解决有关问题;
3、思想目标:通过学习要掌握旋转变换的数学思想;
4、情感目标:在探索中心对称性质的过程中,发展自主学习的能力,培养合作交流的习惯。问题1:什么是中心对称?问题2:什么是对称中心?问题3:什么是对称点?探索概念中心对称:把一个图形绕着某一个点旋转1800,如果它能够与另一个图形重合,那么就是说这两个图形关于这个点对称,也称中心对称。对称中心:这个固定的点叫做对称中心。
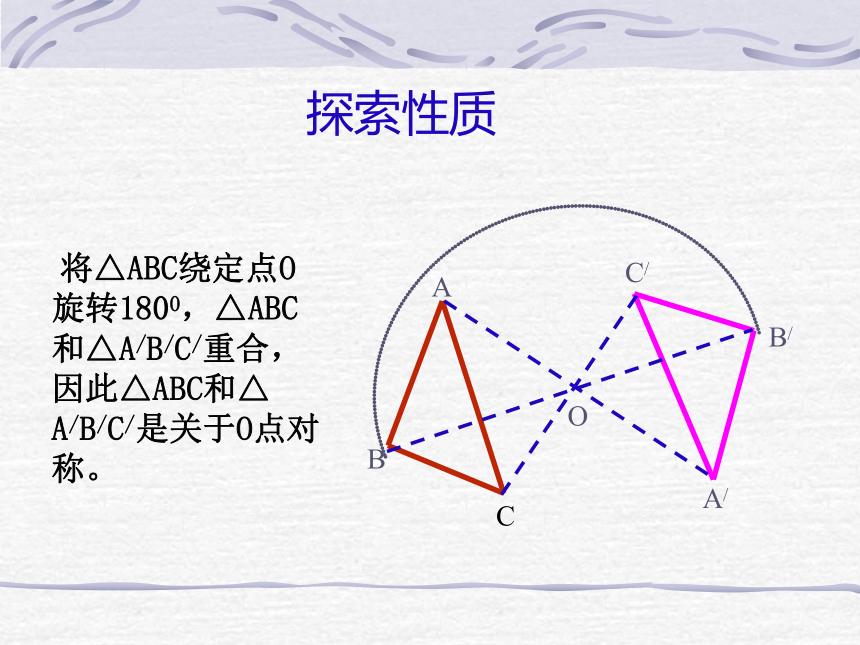
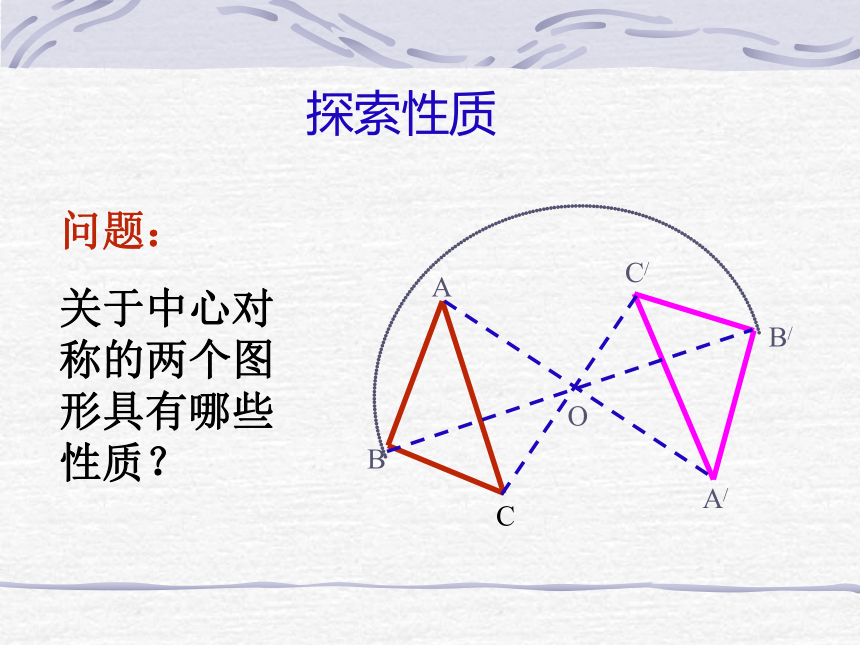
对称点:两个图形的对应点叫做关于中心的对称点。ABCA/B/C/O探索性质 将△ABC绕定点O旋转1800,△ABC和△A/B/C/重合,因此△ABC和△ A/B/C/是关于O点对称。ABCA/B/C/O探索性质 问题:
关于中心对称的两个图形具有哪些性质?性质定理1:关于中心对称的两个图形 是全等形。
定理2:关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。中心对称的判定 逆定理:如果两相图形的对应点连线都经过某一点并且被这一点平分,那么这两个图形关于这一点对称。例题例:已知四边形ABCD和点O(如图),画四边形A/B/C/D/ ,使它与已知四边形关于点O对称。ABCDO画法:1、连结AO并延长到A/,使OA/ =OA,得到A的对称点A/ 。
2、同样画B、C、D的对称点B/ 、C/ 、D/ 。
3、顺次连结A/ 、B/ 、C/ 、D/各点。
四边形A/B/C/D/就是所求的四边形。ABCDA/B/C/D/O(三)知能训练判断正误:
(1)平行四边形的对角顶点关于对角线交点对称。
(2)平行四边形的对边关于对角线的交点对称。
练一练:
(1)已知A点及O点,画A关于O的对称点。
(2)已知线段AB及O,画线段AB关于O的对称线段。
(3)已知△ABC及O,画△ABC关于O的对称三角形。总结归纳1、学生讨论归纳出本节课的重点知识。2、思考中心对称和轴对称的区别,如下表:作业课本P166---3、4。
2、能力目标:经过探讨学习能熟练应用中心对称知识解决有关问题;
3、思想目标:通过学习要掌握旋转变换的数学思想;
4、情感目标:在探索中心对称性质的过程中,发展自主学习的能力,培养合作交流的习惯。问题1:什么是中心对称?问题2:什么是对称中心?问题3:什么是对称点?探索概念中心对称:把一个图形绕着某一个点旋转1800,如果它能够与另一个图形重合,那么就是说这两个图形关于这个点对称,也称中心对称。对称中心:这个固定的点叫做对称中心。
对称点:两个图形的对应点叫做关于中心的对称点。ABCA/B/C/O探索性质 将△ABC绕定点O旋转1800,△ABC和△A/B/C/重合,因此△ABC和△ A/B/C/是关于O点对称。ABCA/B/C/O探索性质 问题:
关于中心对称的两个图形具有哪些性质?性质定理1:关于中心对称的两个图形 是全等形。
定理2:关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。中心对称的判定 逆定理:如果两相图形的对应点连线都经过某一点并且被这一点平分,那么这两个图形关于这一点对称。例题例:已知四边形ABCD和点O(如图),画四边形A/B/C/D/ ,使它与已知四边形关于点O对称。ABCDO画法:1、连结AO并延长到A/,使OA/ =OA,得到A的对称点A/ 。
2、同样画B、C、D的对称点B/ 、C/ 、D/ 。
3、顺次连结A/ 、B/ 、C/ 、D/各点。
四边形A/B/C/D/就是所求的四边形。ABCDA/B/C/D/O(三)知能训练判断正误:
(1)平行四边形的对角顶点关于对角线交点对称。
(2)平行四边形的对边关于对角线的交点对称。
练一练:
(1)已知A点及O点,画A关于O的对称点。
(2)已知线段AB及O,画线段AB关于O的对称线段。
(3)已知△ABC及O,画△ABC关于O的对称三角形。总结归纳1、学生讨论归纳出本节课的重点知识。2、思考中心对称和轴对称的区别,如下表:作业课本P166---3、4。
