第2课时 平面直角坐标系中的轴对称导学案(无答案)
文档属性
| 名称 | 第2课时 平面直角坐标系中的轴对称导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 268.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-20 13:50:29 | ||
图片预览

文档简介
第2课时 平面直角坐标系中的轴对称
【学习目标】
1、了解平面直角坐标系中关于坐标轴对称的两个点的坐标的关系(重点);
2、能在平面直角坐标系中作出简单的平面图形经过一次轴对称变换后的图形并写出对称点的坐标(难点)
【学习过程】
一.学前准备
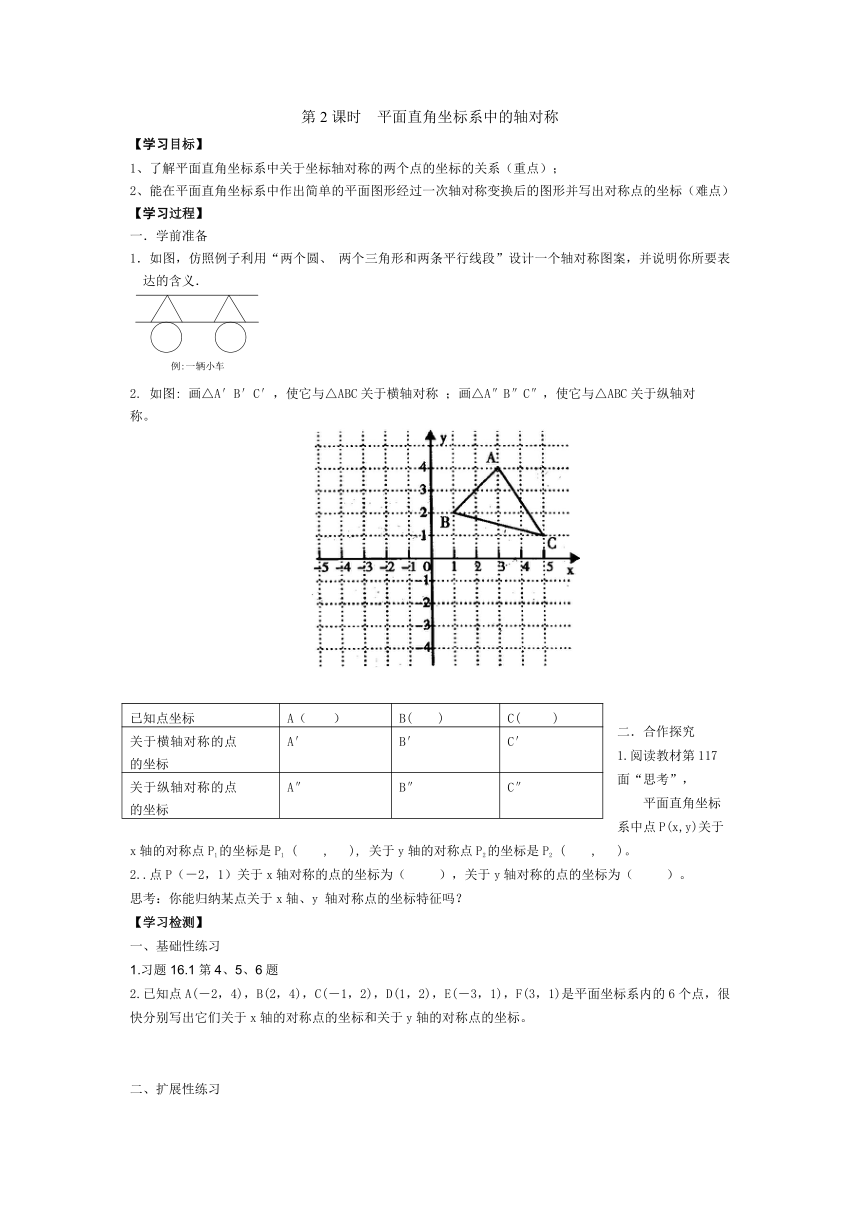
1.如图,仿照例子利用“两个圆、两个三角形和两条平行线段”设计一个轴对称图案,并说明你所要表达的含义.
2. 如图: 画△A′B′C′,使它与△ABC关于横轴对称;画△A″B″C″,使它与△ABC关于纵轴对称。
已知点坐标 A( ) B( ) C( )
关于横轴对称的点的坐标 A′ B′ C′
关于纵轴对称的点的坐标 A″ B″ C″
二.合作探究
1.阅读教材第117面“思考”,
平面直角坐标系中点P(x,y)关于x轴的对称点P1的坐标是P1 ( , ), 关于y轴的对称点P2的坐标是P2 ( , )。
2..点P(-2,1)关于x轴对称的点的坐标为( ),关于y轴对称的点的坐标为( )。
思考:你能归纳某点关于x轴、y 轴对称点的坐标特征吗?
【学习检测】
一、基础性练习
1.习题16.1第4、5、6题
2.已知点A(-2,4),B(2,4),C(-1,2),D(1,2),E(-3,1),F(3,1)是平面坐标系内的6个点,很快分别写出它们关于x轴的对称点的坐标和关于y轴的对称点的坐标。
二、扩展性练习
1. 若点P(2a+b,-3a)与点P′(8,b+2)关于x轴对称,则a = ,b= .
2.平面直角坐标系中长方形ABCD,A(-1,1),B(1,1),C(1,0),D(-1,0),在下左图中画出它关于x轴对称的图形,在下右图中将它向下平移1个单位,这两个变换得到的结果一样吗?
3. 画△A1 B1 C1,,,使它与△ABC关于直线x=1对称.
【学习小结】
1、 我的收获:
2、 我的困惑:
【学习目标】
1、了解平面直角坐标系中关于坐标轴对称的两个点的坐标的关系(重点);
2、能在平面直角坐标系中作出简单的平面图形经过一次轴对称变换后的图形并写出对称点的坐标(难点)
【学习过程】
一.学前准备
1.如图,仿照例子利用“两个圆、两个三角形和两条平行线段”设计一个轴对称图案,并说明你所要表达的含义.
2. 如图: 画△A′B′C′,使它与△ABC关于横轴对称;画△A″B″C″,使它与△ABC关于纵轴对称。
已知点坐标 A( ) B( ) C( )
关于横轴对称的点的坐标 A′ B′ C′
关于纵轴对称的点的坐标 A″ B″ C″
二.合作探究
1.阅读教材第117面“思考”,
平面直角坐标系中点P(x,y)关于x轴的对称点P1的坐标是P1 ( , ), 关于y轴的对称点P2的坐标是P2 ( , )。
2..点P(-2,1)关于x轴对称的点的坐标为( ),关于y轴对称的点的坐标为( )。
思考:你能归纳某点关于x轴、y 轴对称点的坐标特征吗?
【学习检测】
一、基础性练习
1.习题16.1第4、5、6题
2.已知点A(-2,4),B(2,4),C(-1,2),D(1,2),E(-3,1),F(3,1)是平面坐标系内的6个点,很快分别写出它们关于x轴的对称点的坐标和关于y轴的对称点的坐标。
二、扩展性练习
1. 若点P(2a+b,-3a)与点P′(8,b+2)关于x轴对称,则a = ,b= .
2.平面直角坐标系中长方形ABCD,A(-1,1),B(1,1),C(1,0),D(-1,0),在下左图中画出它关于x轴对称的图形,在下右图中将它向下平移1个单位,这两个变换得到的结果一样吗?
3. 画△A1 B1 C1,,,使它与△ABC关于直线x=1对称.
【学习小结】
1、 我的收获:
2、 我的困惑:
