1.2.2 绝对值不等式的解法 课件2
文档属性
| 名称 | 1.2.2 绝对值不等式的解法 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-20 00:00:00 | ||
图片预览






文档简介
课件15张PPT。第一讲 不等式和绝对值不等式
1.2 绝对值不等式
1.2.2 绝对值不等式的解法(一)会利用绝对值的几何意义求解以下类型的不等式:
①|ax+b|≤c; ②|ax+b|≥c.含有绝对值的不等式的两种基本的类型
第一种类型:设a为正数.根据绝对值的意义,不等式|x|<a的解集是{x|-a<x<a},它的几何意义就是数轴上到原点的距离小于a的点的集合,是开区间(-a,a),如下图所示.
如果给定的不等式符合上述形式,就可以直接利用它的结果来解.思考1 |x|<1的解集为________.
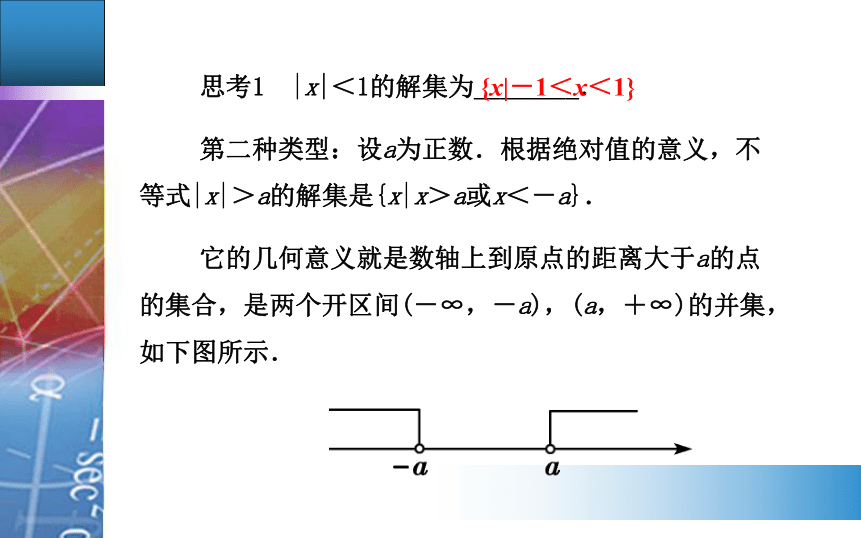
第二种类型:设a为正数.根据绝对值的意义,不等式|x|>a的解集是{x|x>a或x<-a}.
它的几何意义就是数轴上到原点的距离大于a的点的集合,是两个开区间(-∞,-a),(a,+∞)的并集,如下图所示.
{x|-1<x<1}同样,如果给定的不等式符合这种类型,就可以直接利用它的结果来解.
思考2 |x|>1的解集为________.{x|x<-1或x>1}题型一 |ax+b|≤e(或|ax+b|≥e)(e>0)型,不等式的解法变 式训 练1.解下列不等式.
(1)|1-2x|>5;
(2)|4x-1|+2≤10.题型二 绝对值不等式的综合性问题变 式训 练2.x2-2|x|-15>0的解集是________.解析:∵|x|2-2|x|-15>0,
∴|x|>5或|x|<-3(舍去).
∴x<-5或x>5.
故不等式的解集为{x|x<-5或x>5}.
答案:{x|x<-5或x>5}
1.2 绝对值不等式
1.2.2 绝对值不等式的解法(一)会利用绝对值的几何意义求解以下类型的不等式:
①|ax+b|≤c; ②|ax+b|≥c.含有绝对值的不等式的两种基本的类型
第一种类型:设a为正数.根据绝对值的意义,不等式|x|<a的解集是{x|-a<x<a},它的几何意义就是数轴上到原点的距离小于a的点的集合,是开区间(-a,a),如下图所示.
如果给定的不等式符合上述形式,就可以直接利用它的结果来解.思考1 |x|<1的解集为________.
第二种类型:设a为正数.根据绝对值的意义,不等式|x|>a的解集是{x|x>a或x<-a}.
它的几何意义就是数轴上到原点的距离大于a的点的集合,是两个开区间(-∞,-a),(a,+∞)的并集,如下图所示.
{x|-1<x<1}同样,如果给定的不等式符合这种类型,就可以直接利用它的结果来解.
思考2 |x|>1的解集为________.{x|x<-1或x>1}题型一 |ax+b|≤e(或|ax+b|≥e)(e>0)型,不等式的解法变 式训 练1.解下列不等式.
(1)|1-2x|>5;
(2)|4x-1|+2≤10.题型二 绝对值不等式的综合性问题变 式训 练2.x2-2|x|-15>0的解集是________.解析:∵|x|2-2|x|-15>0,
∴|x|>5或|x|<-3(舍去).
∴x<-5或x>5.
故不等式的解集为{x|x<-5或x>5}.
答案:{x|x<-5或x>5}
