1.2.1 绝对值三角不等式 教案
文档属性
| 名称 | 1.2.1 绝对值三角不等式 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 135.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-20 16:00:03 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.2.1
绝对值三角不等式
教案
教学目标
1.了解绝对值三角不等式的含义,理解绝对值三角不等式公式及推导方法,
会进行简
单的应用.
2.充分运用观察、类比、猜想、分析证明的数学思维方法,体会转化和数形结合的数学
思想,并能运用绝对值三角不等式公式进行推理和证明.
教学重、难点
重点:绝对值三角不等式的含义,绝对值三角不等式的理解和运用.
难点:绝对值三角不等式的发现和推导、取等条件.
教学过程
一、复习引入:
关于含有绝对值的不等式的问题,主要包括两类:一类是解不等式,另一类是证明不等式.本节课探讨不等式证明这类问题.
1.请同学们回忆一下绝对值的意义.
.
几何意义:在数轴上,一个点到原点的距离称为这个点所表示的数的绝对值.
2.证明一个含有绝对值的不等式成立,除了要应用一般不等式的基本性质之外,经常还要用到关于绝对值的和、差、积、商的性质:
(1),当且仅当时等号成立,当且仅当
时等号成立.
(2),
(3),
(4)
那么
二、讲解新课:
探究:之间有什么关系?
结论:(当且仅当ab≥0时,等号成立.)
定理1
a,b如果
是实数,则(当且仅当ab≥0时,等号成立.)
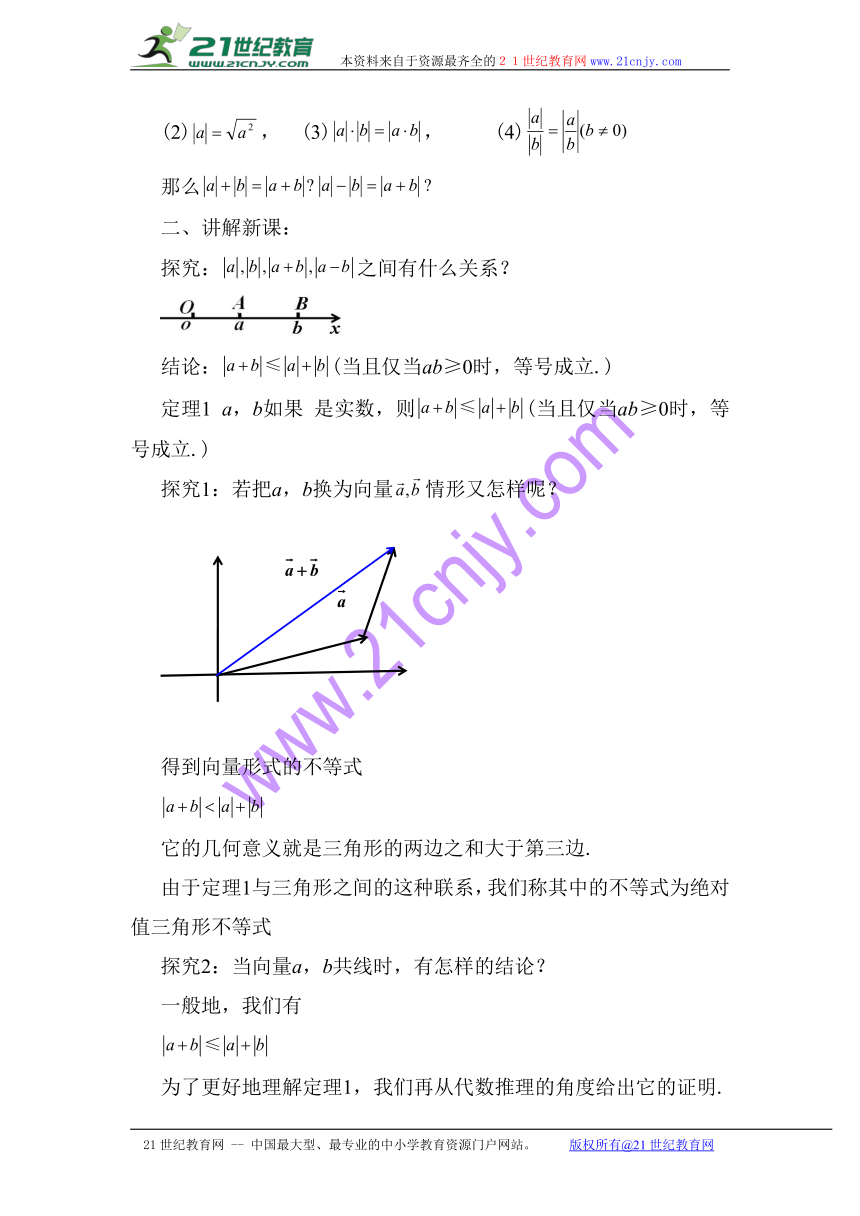
探究1:若把a,b换为向量情形又怎样呢?
得到向量形式的不等式
它的几何意义就是三角形的两边之和大于第三边.
由于定理1与三角形之间的这种联系,我们称其中的不等式为绝对值三角形不等式
探究2:当向量a,b共线时,有怎样的结论?
一般地,我们有
为了更好地理解定理1,我们再从代数推理的角度给出它的证明.
证明:(1)当ab≥0时,
(2)当ab<0时,
综合(1)(2)知定理成立.
根据定理1,有,就是,所以,.
即:如果a,b是实数,则
以上我们讨论了关于两个实数的绝对值不等式,这是最基本、最重要的绝对值不等式.根据这样思想方法,我们可以讨论涉及多个实数的绝对值不等式问题.例如,我们有21教育网
定理2
如果a、b、c是实数,那么,当且仅当时,等号成立.
思考:如何利用数轴给出定理2的几何解释?
(设A,B,C为数轴上的3个点,分别表示数a,b,c,则线段当且仅当C在A,B之间时,等号成立.)
三、典型例题:
例2
两个施工队分别被安排在公路沿线的两个地点施工,这两个地点分别位于公路路碑的第10公里和第20公里处.现要在公路沿线建两个施工队的共同临时生活区,每个施工队每天在生活区和施工地点之间往返一次,要使两个施工队每天往返的路程之和最小,生活区应该建于何处?21世纪教育网版权所有
四、课堂小结:
1.定理1
2.绝对值三角不等式的几种形式,以及取等号的条件.
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
1.2.1
绝对值三角不等式
教案
教学目标
1.了解绝对值三角不等式的含义,理解绝对值三角不等式公式及推导方法,
会进行简
单的应用.
2.充分运用观察、类比、猜想、分析证明的数学思维方法,体会转化和数形结合的数学
思想,并能运用绝对值三角不等式公式进行推理和证明.
教学重、难点
重点:绝对值三角不等式的含义,绝对值三角不等式的理解和运用.
难点:绝对值三角不等式的发现和推导、取等条件.
教学过程
一、复习引入:
关于含有绝对值的不等式的问题,主要包括两类:一类是解不等式,另一类是证明不等式.本节课探讨不等式证明这类问题.
1.请同学们回忆一下绝对值的意义.
.
几何意义:在数轴上,一个点到原点的距离称为这个点所表示的数的绝对值.
2.证明一个含有绝对值的不等式成立,除了要应用一般不等式的基本性质之外,经常还要用到关于绝对值的和、差、积、商的性质:
(1),当且仅当时等号成立,当且仅当
时等号成立.
(2),
(3),
(4)
那么
二、讲解新课:
探究:之间有什么关系?
结论:(当且仅当ab≥0时,等号成立.)
定理1
a,b如果
是实数,则(当且仅当ab≥0时,等号成立.)
探究1:若把a,b换为向量情形又怎样呢?
得到向量形式的不等式
它的几何意义就是三角形的两边之和大于第三边.
由于定理1与三角形之间的这种联系,我们称其中的不等式为绝对值三角形不等式
探究2:当向量a,b共线时,有怎样的结论?
一般地,我们有
为了更好地理解定理1,我们再从代数推理的角度给出它的证明.
证明:(1)当ab≥0时,
(2)当ab<0时,
综合(1)(2)知定理成立.
根据定理1,有,就是,所以,.
即:如果a,b是实数,则
以上我们讨论了关于两个实数的绝对值不等式,这是最基本、最重要的绝对值不等式.根据这样思想方法,我们可以讨论涉及多个实数的绝对值不等式问题.例如,我们有21教育网
定理2
如果a、b、c是实数,那么,当且仅当时,等号成立.
思考:如何利用数轴给出定理2的几何解释?
(设A,B,C为数轴上的3个点,分别表示数a,b,c,则线段当且仅当C在A,B之间时,等号成立.)
三、典型例题:
例2
两个施工队分别被安排在公路沿线的两个地点施工,这两个地点分别位于公路路碑的第10公里和第20公里处.现要在公路沿线建两个施工队的共同临时生活区,每个施工队每天在生活区和施工地点之间往返一次,要使两个施工队每天往返的路程之和最小,生活区应该建于何处?21世纪教育网版权所有
四、课堂小结:
1.定理1
2.绝对值三角不等式的几种形式,以及取等号的条件.
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
