2.3 反证法与放缩法 同步练习1(含答案)
文档属性
| 名称 | 2.3 反证法与放缩法 同步练习1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 134.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-20 00:00:00 | ||
图片预览




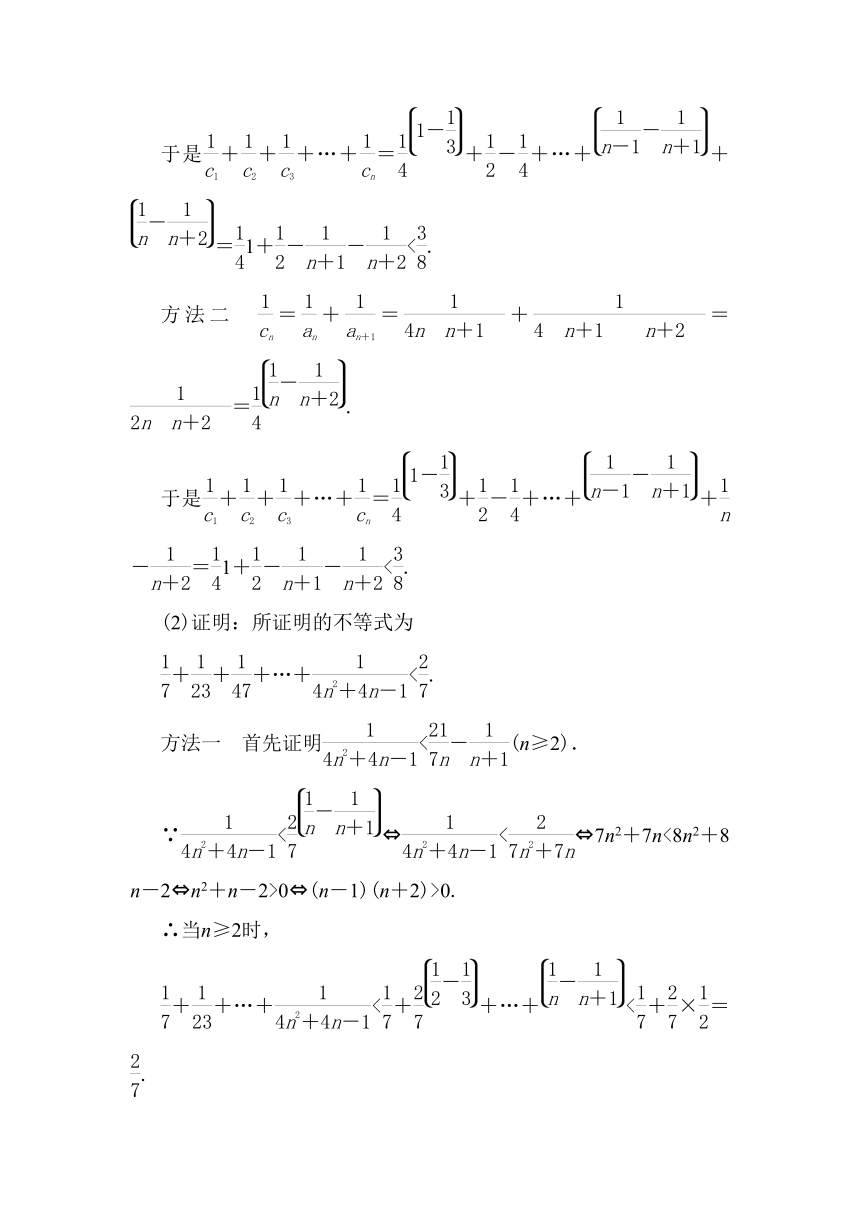
文档简介
2.3
反证法与放缩法
同步练习
1.用反证法证明“若整系数一元二次方程ax2+bx+c=0(a≠0)有有理根,那么a,b,c中至少有一个偶数”时,下列假设中正确的是( )
A.假设a,b,c都是偶数
B.假设a,b,c都不是偶数
C.假设a,b,c至多有一个偶数
D.假设a,b,c至多有两个偶数
答案:B
2.在求证“数列,,不可能为等比数列”时最好采用( )
A.分析法
B.综合法
C.反证法
D.直接法
答案:C
3.设M=+++…+,则( )
A.M=1
B.M<1
C.M>1
D.M与1大小关系不定
答案:B
4.a,b,c,d∈R,a2+b2=1,c2+d2=1,则abcd的最小值等于( )
A.
B.-
C.
D.-
答案:B
5.A=1+++…+与(n∈N
)的大小关系为________.
解析:n∈N
,当n=1时,A==1;
当n>1时,A=1+++…+>1+++…+=1+(-1)+(-)+…+(-)=.
综上可知,A≥.
答案:A≥
6.设a,b,c∈R+,则三个数a+,b+,c+( )
A.都大于2
B.都小于2
C.至少有一个不大于2
D.至少有一个不小于2
答案:D
7.若正数a,b满足ab≥1+a+b,则a+b的最小值为________.
答案:2+2
8.A=1+++…+与2的大小关系是________.
解析:A=1+++…+<1+++…+=1+++…+=2-<2.
答案:A<2
9.已知x,y>0,且x+y>2.
证明:,中至少有一个小于2.
证明:(反证法)设≥2,≥2,则
由①②式可得2+x+y≥2(x+y),
即x+y≤2与题设矛盾.
∴,中至少有一个小于2.
10.若数列{xn}的通项公式为xn=,求证:x1·x3·x5·…·x2n-1<.
证明:∵==,
x1·x3·x5·…·x2n-1=××…×<=.
∴x1·x3·x5·…·x2n-1<
.
11.数列{an}的通项公式an=4n(n+1).
(1)记=+,求证:对一切正整数n,有+++…+<.
(2)求证:对一切正整数n,有+++…+<.
答案:(1)证明:方法一 ==-,
所以=+=.
于是+++…+=+-+…++=1+--<.
方法二 =+=+==.
于是+++…+=+-+…++-=1+--<.
(2)证明:所证明的不等式为
+++…+<.
方法一 首先证明<-(n≥2).
∵< < 7n2+7n<8n2+8n-2 n2+n-2>0 (n-1)(n+2)>0.
∴当n≥2时,
++…+<++…+<+×=.
当n=1时,<.
综上所述,对一切正整数n,有
+++…+<.
方法二 <==.
当n≥3时,++…+<++++…++<++<++=.
当n=1时,<;
当n=2时,+<+=.
综上所述,对一切正整数n,有
+++…+<.
12.若数列{an}的通项公式为an=n2,n∈N
,求证:对一切正整数n,有++…+<.
证明:①当n=1时,=1<,∴原不等式成立.
②当n=2时,
+=1+<,∴原不等式成立.
③当n≥3时,
∵n2>(n-1)·(n+1),∴<.
++…+=++…++<1+++…++=1++++…++=1+1-+-+-+…+--=1+=+--<.
∴当n≥3时,∴原不等式成立.
综上,对一切正整数n,有++…+<.
13.正项数列{an}的通项公式an=2n,令bn=,数列{bn}的前n项和为Tn.求证:对于任意的n∈N
,都有Tn<.
证明:由于an=2n,bn=.
则bn==.
Tn=1-+-+-+…+-+-=1+--<=.
14.设数列{an}的前n项和为Sn,满足2Sn=an+1-2n+1+1(n∈N
),且a1,a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)求证:对一切正整数n,有++…+<.
解析:(1)2Sn=an+1-2n+1+1,2Sn+1=an+2-2n+2+1
相减得:an+2=3an+1+2n+1
而2S1=a2-3 a2=2a1+3,则a3=3a2+4=6a1+13
故a1,a2+5,a3成等差数列
a1+a3=2(a2+5) a1=1.
(2)a1=1,a2=5,得an+1=3an+2n对 n∈N
均成立.
an+1=3an+2n an+1+2n+1=3(an+2n)得
an+2n=3(an-1+2n-1)=32(an-2+2n-2)=…=3n-1(a1+2) an=3n-2n.
(3)当n=1时,=1<;
当n≥2时,
n≥2>2 3n>2×2n an>2n <.
++…+<1+++…+=1+-<,
由上式得:对一切正整数n,有
++…+<.
15.设an是函数f(x)=x3+n2x-1(n∈N
)的零点,且0证明:先证明左边的不等式:
因为a+n2an-1=0.
由0所以an>.所以
a1+a2+…+an>++…+.
以下证明++…+≥.①
因为an>≥=-,
所以
a1+a2+…+an>+++…+=1-=.
不等式①对应任何n∈N
都成立.所以
a1+a2+…+an>.
再证明右边的不等式:
当n=1时,f(x)=x3+x-1.
由于f=3+-1=-<0,
f=3+-1=>0,
所以由(1)知0因为当n≥2时,<=-,
所以当n≥2时,
a1+a2+a3+a4+…+an<++++…+=1+-<.
所以当n∈N
时,都有a1+a2+…+an<.
综上所述,
反证法与放缩法
同步练习
1.用反证法证明“若整系数一元二次方程ax2+bx+c=0(a≠0)有有理根,那么a,b,c中至少有一个偶数”时,下列假设中正确的是( )
A.假设a,b,c都是偶数
B.假设a,b,c都不是偶数
C.假设a,b,c至多有一个偶数
D.假设a,b,c至多有两个偶数
答案:B
2.在求证“数列,,不可能为等比数列”时最好采用( )
A.分析法
B.综合法
C.反证法
D.直接法
答案:C
3.设M=+++…+,则( )
A.M=1
B.M<1
C.M>1
D.M与1大小关系不定
答案:B
4.a,b,c,d∈R,a2+b2=1,c2+d2=1,则abcd的最小值等于( )
A.
B.-
C.
D.-
答案:B
5.A=1+++…+与(n∈N
)的大小关系为________.
解析:n∈N
,当n=1时,A==1;
当n>1时,A=1+++…+>1+++…+=1+(-1)+(-)+…+(-)=.
综上可知,A≥.
答案:A≥
6.设a,b,c∈R+,则三个数a+,b+,c+( )
A.都大于2
B.都小于2
C.至少有一个不大于2
D.至少有一个不小于2
答案:D
7.若正数a,b满足ab≥1+a+b,则a+b的最小值为________.
答案:2+2
8.A=1+++…+与2的大小关系是________.
解析:A=1+++…+<1+++…+=1+++…+=2-<2.
答案:A<2
9.已知x,y>0,且x+y>2.
证明:,中至少有一个小于2.
证明:(反证法)设≥2,≥2,则
由①②式可得2+x+y≥2(x+y),
即x+y≤2与题设矛盾.
∴,中至少有一个小于2.
10.若数列{xn}的通项公式为xn=,求证:x1·x3·x5·…·x2n-1<.
证明:∵==,
x1·x3·x5·…·x2n-1=××…×<=.
∴x1·x3·x5·…·x2n-1<
.
11.数列{an}的通项公式an=4n(n+1).
(1)记=+,求证:对一切正整数n,有+++…+<.
(2)求证:对一切正整数n,有+++…+<.
答案:(1)证明:方法一 ==-,
所以=+=.
于是+++…+=+-+…++=1+--<.
方法二 =+=+==.
于是+++…+=+-+…++-=1+--<.
(2)证明:所证明的不等式为
+++…+<.
方法一 首先证明<-(n≥2).
∵< < 7n2+7n<8n2+8n-2 n2+n-2>0 (n-1)(n+2)>0.
∴当n≥2时,
++…+<++…+<+×=.
当n=1时,<.
综上所述,对一切正整数n,有
+++…+<.
方法二 <==.
当n≥3时,++…+<++++…++<++<++=.
当n=1时,<;
当n=2时,+<+=.
综上所述,对一切正整数n,有
+++…+<.
12.若数列{an}的通项公式为an=n2,n∈N
,求证:对一切正整数n,有++…+<.
证明:①当n=1时,=1<,∴原不等式成立.
②当n=2时,
+=1+<,∴原不等式成立.
③当n≥3时,
∵n2>(n-1)·(n+1),∴<.
++…+=++…++<1+++…++=1++++…++=1+1-+-+-+…+--=1+=+--<.
∴当n≥3时,∴原不等式成立.
综上,对一切正整数n,有++…+<.
13.正项数列{an}的通项公式an=2n,令bn=,数列{bn}的前n项和为Tn.求证:对于任意的n∈N
,都有Tn<.
证明:由于an=2n,bn=.
则bn==.
Tn=1-+-+-+…+-+-=1+--<=.
14.设数列{an}的前n项和为Sn,满足2Sn=an+1-2n+1+1(n∈N
),且a1,a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)求证:对一切正整数n,有++…+<.
解析:(1)2Sn=an+1-2n+1+1,2Sn+1=an+2-2n+2+1
相减得:an+2=3an+1+2n+1
而2S1=a2-3 a2=2a1+3,则a3=3a2+4=6a1+13
故a1,a2+5,a3成等差数列
a1+a3=2(a2+5) a1=1.
(2)a1=1,a2=5,得an+1=3an+2n对 n∈N
均成立.
an+1=3an+2n an+1+2n+1=3(an+2n)得
an+2n=3(an-1+2n-1)=32(an-2+2n-2)=…=3n-1(a1+2) an=3n-2n.
(3)当n=1时,=1<;
当n≥2时,
n≥2>2 3n>2×2n an>2n <.
++…+<1+++…+=1+-<,
由上式得:对一切正整数n,有
++…+<.
15.设an是函数f(x)=x3+n2x-1(n∈N
)的零点,且0
因为a+n2an-1=0.
由0
a1+a2+…+an>++…+.
以下证明++…+≥.①
因为an>≥=-,
所以
a1+a2+…+an>+++…+=1-=.
不等式①对应任何n∈N
都成立.所以
a1+a2+…+an>.
再证明右边的不等式:
当n=1时,f(x)=x3+x-1.
由于f=3+-1=-<0,
f=3+-1=>0,
所以
所以当n≥2时,
a1+a2+a3+a4+…+an<++++…+=1+-<.
所以当n∈N
时,都有a1+a2+…+an<.
综上所述,
