18.1.2平行四边形的判定2---三角形中位线定理课件
文档属性
| 名称 | 18.1.2平行四边形的判定2---三角形中位线定理课件 |  | |
| 格式 | zip | ||
| 文件大小 | 146.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-20 21:18:09 | ||
图片预览


文档简介
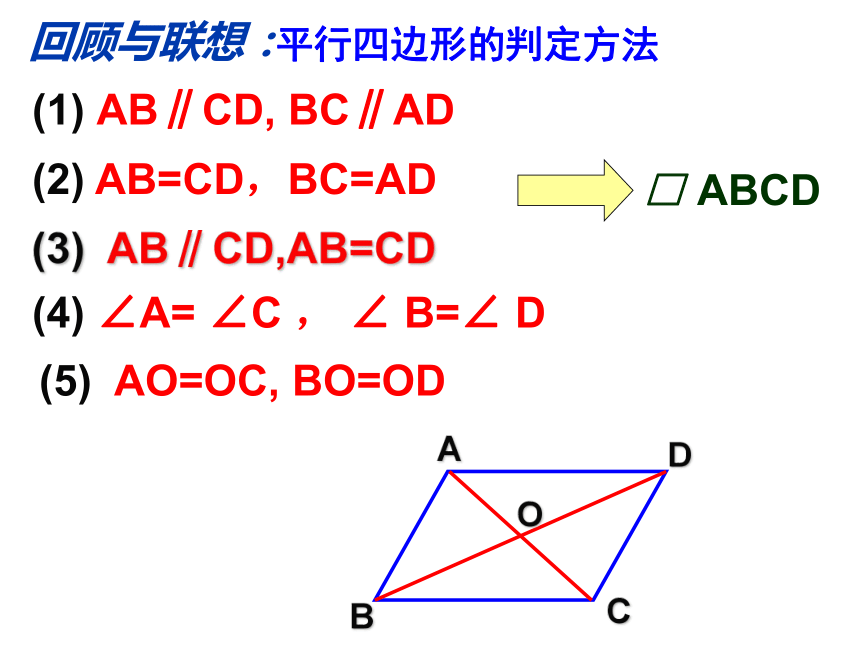
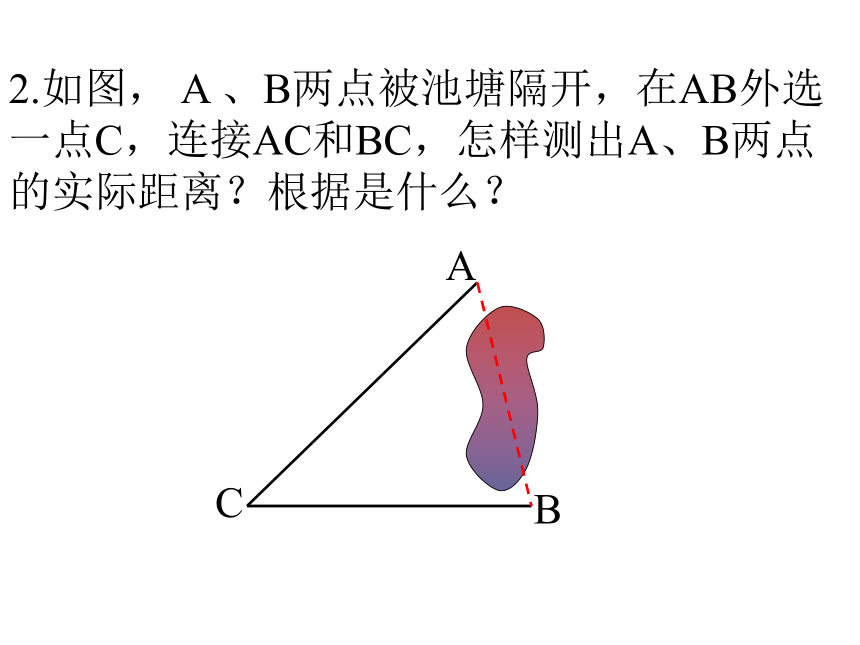
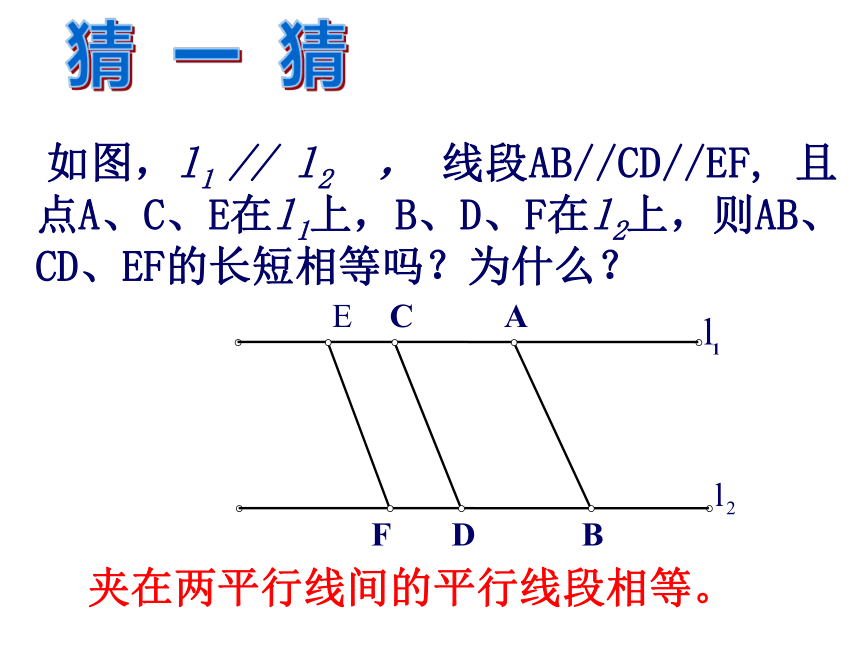
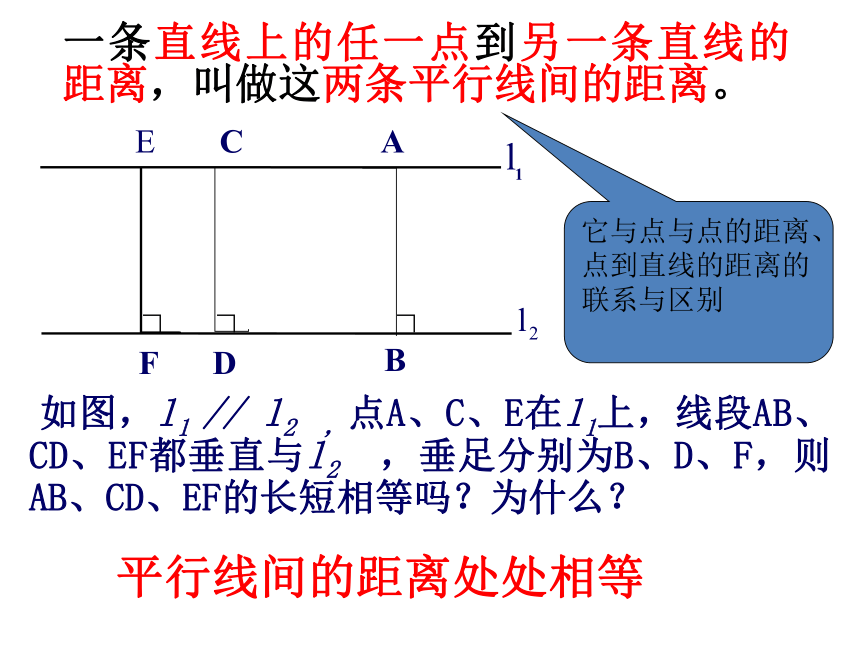
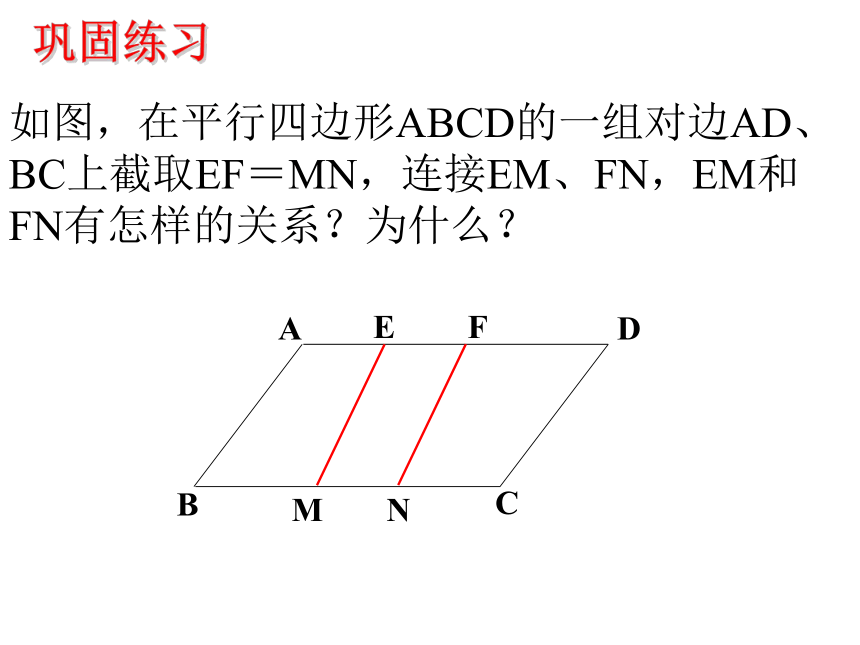
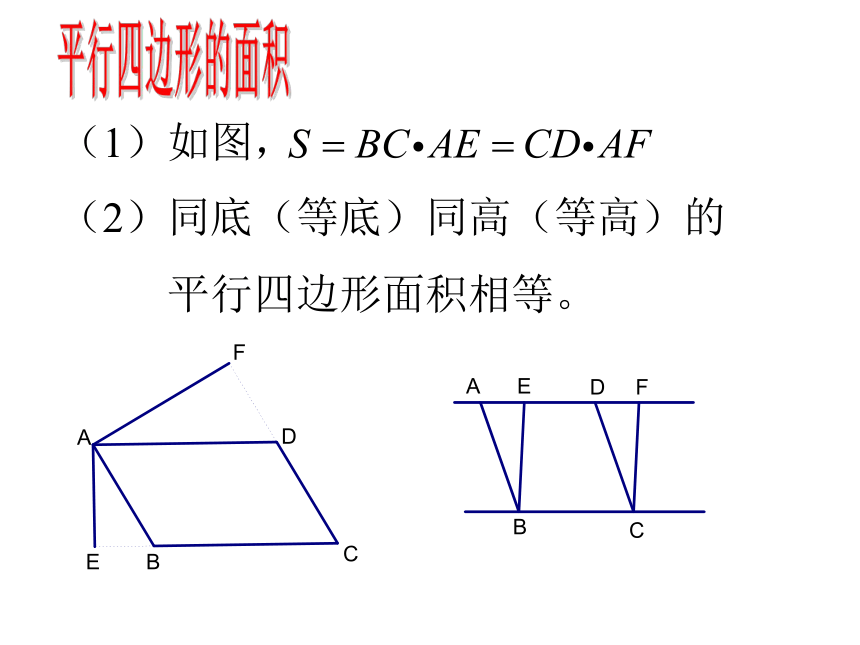
课件34张PPT。18.1.2 平行四边形的判定(3)新人教版八(下)第19章四边形课件三角形中位线定理从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形平行四边形的判定方法 温故知新回顾与联想:□ ABCD(1) AB∥CD, BC∥AD(2) AB=CD,BC=AD(4) ∠A= ∠C , ∠ B=∠ D(5) AO=OC, BO=OD(3) AB∥CD,AB=CDABCDO平行四边形的判定方法2.如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?ABC 如图,l1 // l2 , 线段AB//CD//EF, 且点A、C、E在l1上,B、D、F在l2上,则AB、CD、EF的长短相等吗?为什么?猜 一 猜夹在两平行线间的平行线段相等。∟∟∟ 如图,l1 // l2 ,点A、C、E在l1上,线段AB、CD、EF都垂直与l2 ,垂足分别为B、D、F,则AB、CD、EF的长短相等吗?为什么?一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离。平行线间的距离处处相等它与点与点的距离、点到直线的距离的联系与区别如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?巩固练习平行四边形的面积(1)如图,(2)同底(等底)同高(等高)的
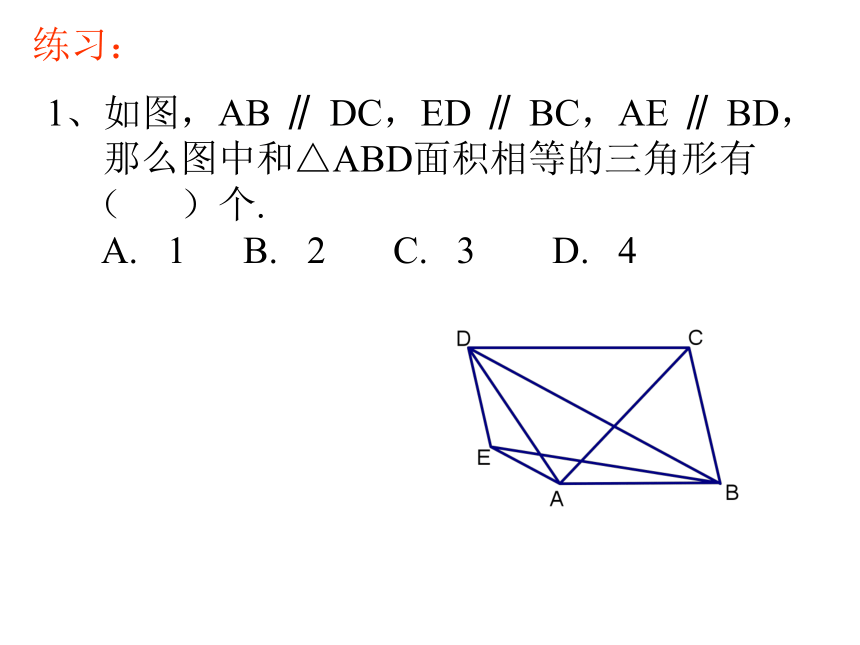
平行四边形面积相等。练习:1、如图,AB ∥ DC,ED ∥ BC,AE ∥ BD,
那么图中和△ABD面积相等的三角形有
( )个.
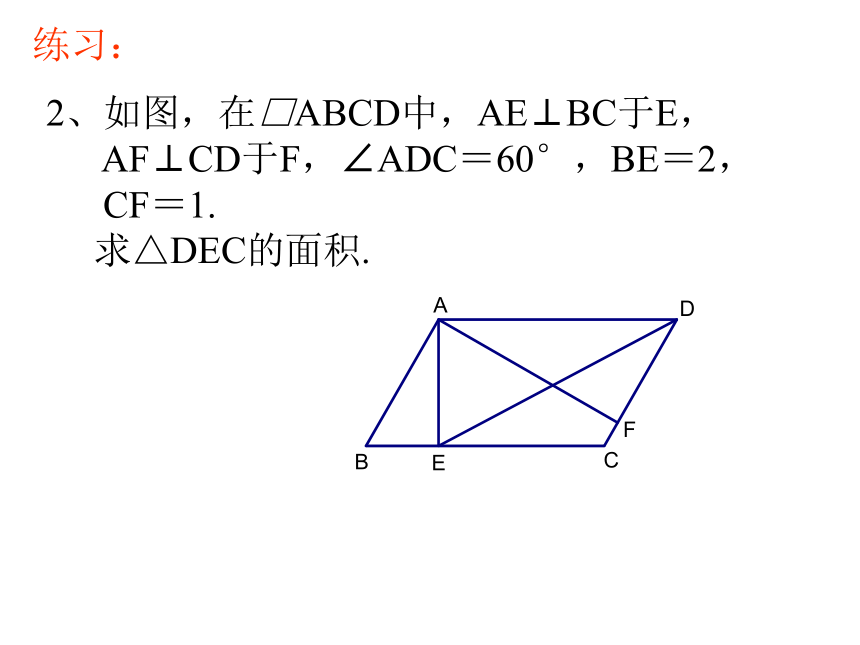
A. 1 B. 2 C. 3 D. 4练习:2、如图,在□ABCD中,AE⊥BC于E,
AF⊥CD于F,∠ADC=60°,BE=2,
CF=1.
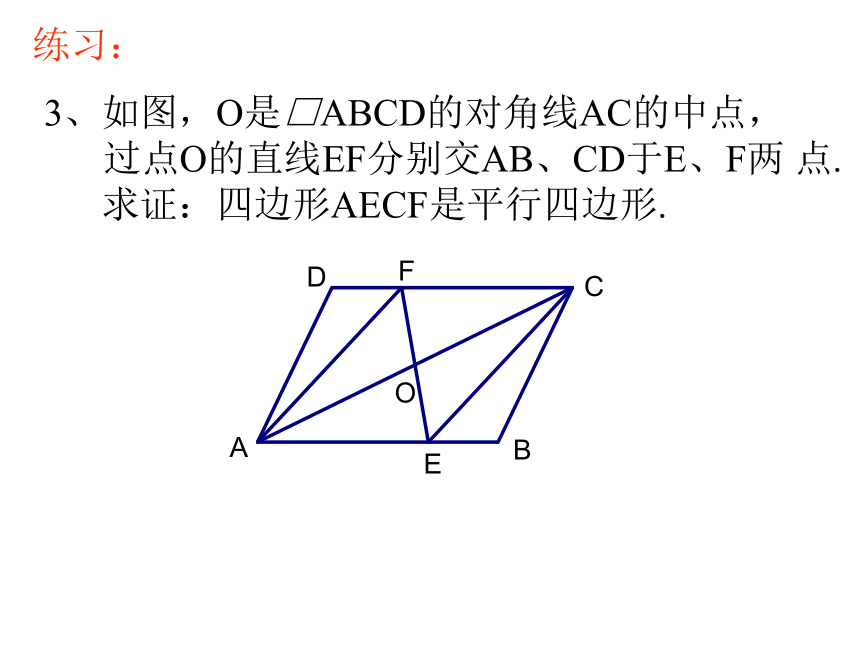
求△DEC的面积.练习:3、如图,O是□ABCD的对角线AC的中点,
过点O的直线EF分别交AB、CD于E、F两 点.
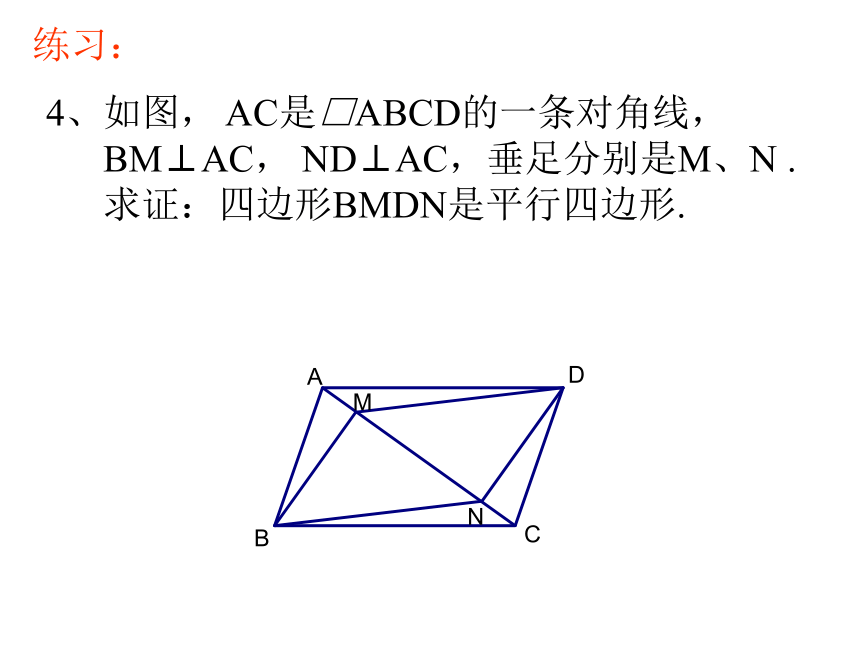
求证:四边形AECF是平行四边形.练习:4、如图, AC是□ABCD的一条对角线,
BM⊥AC, ND⊥AC,垂足分别是M、N .
求证:四边形BMDN是平行四边形.练习:5、如图,在□ABCD中,延长AD到F,使
DF=AD,连结BF交CD于点E .
求证:点E平分CD与BF.练习:6、如图,已知E为□ABCD中DC延长线上的
一 点,且CE=DC,连结AE,分别交BC、
BD于点F、G,连结AC交BD于点O,连结
OF .
求证:AB=2OF.现有一张三角形纸片,你能通过裁剪,将它拼成一个平行四边形吗?创设情境问题1:需要把三角形剪成几块?问题2:如何将剪开的部分拼成一个平行四边形?ABCFABCDEF∵DE=EF 、∠AED=∠CEF 、AE=EC∴△ADE ≌ △CFE证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.∴AD=FC 、∠A=∠ECF
∴AB∥FC又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形还有另外的证法吗?∴DF∥BC,DF=BC又∵即DE∥BC例1、如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC位置关系数量关系2DE=BCF证明:延长DE到F,使EF=DE,连接FC、DC、AF。∵AE=EC,又EF=DE∴四边形ADCF 是平行四边形∴CF DA,即CF BD∴四边形DBCF是平行四边形。∴DF BC又DE= DF, ∴DE∥BC,且DE= BC例1、如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC证法二连结三角形两边中点的线段叫三角形的中位线DE是△ABC的中位线定义:三角形中位线定理三角形的中位线平行于三角形的第三边,并且等于第三边的一半FE1、一个三角形有几条中位线?D思考:2.三角形的中位线与三角形的中线有什么区别?B中位线是两个中点的连线,
而中线是一个顶点和对边中点的连线。CAFEDACB三角形的中位线与三角形的中线有什么区别?思考:三角形的中位线平行于三角形的第三边,并且等于第三边的一半三角形中位线定理BCDEA三角形中位线定理有何作用?证明:连接DE、DF
∵AD是△ABC的中线,EF是中位线,
∴点D、E、F分别是BC、AB、AC的中点
∴ DE、DF也是△ABC的中位线
∴DE∥AC,DF∥ AB
(三角形的中位线的定义)
∴四边形AEDF是平行四边形
(平行四边形的定义)
∴ AD与EF互相平分
(平行四边形的对角线互相平分)1、已知,如图AD是△ABC的中线,EF是中位线,求证:AD与EF互相平分练一练(1)△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.AEDCB(1)(2) △ABC中,D、E分别是AB、AC的中点,∠A=50°, ∠B=70°,则∠AED=_____.练一练2、填空题5cm10560°50°70°60°60°(4)三角形的周长为18cm,面积为48cm2 ,这个三角形的三条中位线围成三角形的周长是 ,面积是 .(3)如图,E是平行四边形ABCD的AB边上的中点,且AD=10cm,那么OE= cm.5练一练2、填空题9cm10512cm2①图中有几个平行四边形?②图中有几个三角形?它们有什么关系?思考:(5)如图:如果AD= AB,AE= AC,
DE=2cm,那么BC= cm。ACDBE(6)在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是 。811练一练2、填空题248381.51.544四边形EFGH
是平行四边形吗?顺次连结四边形各边中点所得的四边形是平行四边形已知:E、F、G、H分别是四边形ABCD中AB、 BC、CD、DA的中点。
求证:EFGH是平行四边形。例2、求证:实践应用3、如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?ABC练一练求证:DE=EF挑战自我: 4.已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN。D,E,F分别是MB,BC,CN的中点,连结DE,EF。练一练1.三角形的中位线定义.2.三角形的中位线定理.3. 在三角形中给出一边的中点时,通常要转化为中位线来解题.4.线段的倍分要转化为相等问题来解决.5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)小结巩固新知
1.三角形的中位线_______第三边,并且______第三边的____________
2.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=——
3.若等腰△ABC的周长是40cm,AB=AC=14cm,则中位线DE=———60°4ABCDED 8cm6cm 平行于
等于 一半 4.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,
若MN =12 ,则BC = . 61°24 5. 如图, △ABC 中, D ,E 分别为AB,
AC 的中点,当BC =10㎝时,则DE = .5㎝ 6.如图,已知△ABC中,
AB = 3㎝,BC=3.4 ㎝ AC=4㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长
是 ㎝.
5.27、如下图:在Rt △ ABC中,∠A=90°,D、E、F分别是各边中点, AB=6cm,AC=8cm,则△DEF的周长= cm。12EFBACD
平行四边形面积相等。练习:1、如图,AB ∥ DC,ED ∥ BC,AE ∥ BD,
那么图中和△ABD面积相等的三角形有
( )个.
A. 1 B. 2 C. 3 D. 4练习:2、如图,在□ABCD中,AE⊥BC于E,
AF⊥CD于F,∠ADC=60°,BE=2,
CF=1.
求△DEC的面积.练习:3、如图,O是□ABCD的对角线AC的中点,
过点O的直线EF分别交AB、CD于E、F两 点.
求证:四边形AECF是平行四边形.练习:4、如图, AC是□ABCD的一条对角线,
BM⊥AC, ND⊥AC,垂足分别是M、N .
求证:四边形BMDN是平行四边形.练习:5、如图,在□ABCD中,延长AD到F,使
DF=AD,连结BF交CD于点E .
求证:点E平分CD与BF.练习:6、如图,已知E为□ABCD中DC延长线上的
一 点,且CE=DC,连结AE,分别交BC、
BD于点F、G,连结AC交BD于点O,连结
OF .
求证:AB=2OF.现有一张三角形纸片,你能通过裁剪,将它拼成一个平行四边形吗?创设情境问题1:需要把三角形剪成几块?问题2:如何将剪开的部分拼成一个平行四边形?ABCFABCDEF∵DE=EF 、∠AED=∠CEF 、AE=EC∴△ADE ≌ △CFE证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.∴AD=FC 、∠A=∠ECF
∴AB∥FC又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形还有另外的证法吗?∴DF∥BC,DF=BC又∵即DE∥BC例1、如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC位置关系数量关系2DE=BCF证明:延长DE到F,使EF=DE,连接FC、DC、AF。∵AE=EC,又EF=DE∴四边形ADCF 是平行四边形∴CF DA,即CF BD∴四边形DBCF是平行四边形。∴DF BC又DE= DF, ∴DE∥BC,且DE= BC例1、如图,点D、E分别是△ABC的边AB、AC的中点,求证DE∥BC且DE= BC证法二连结三角形两边中点的线段叫三角形的中位线DE是△ABC的中位线定义:三角形中位线定理三角形的中位线平行于三角形的第三边,并且等于第三边的一半FE1、一个三角形有几条中位线?D思考:2.三角形的中位线与三角形的中线有什么区别?B中位线是两个中点的连线,
而中线是一个顶点和对边中点的连线。CAFEDACB三角形的中位线与三角形的中线有什么区别?思考:三角形的中位线平行于三角形的第三边,并且等于第三边的一半三角形中位线定理BCDEA三角形中位线定理有何作用?证明:连接DE、DF
∵AD是△ABC的中线,EF是中位线,
∴点D、E、F分别是BC、AB、AC的中点
∴ DE、DF也是△ABC的中位线
∴DE∥AC,DF∥ AB
(三角形的中位线的定义)
∴四边形AEDF是平行四边形
(平行四边形的定义)
∴ AD与EF互相平分
(平行四边形的对角线互相平分)1、已知,如图AD是△ABC的中线,EF是中位线,求证:AD与EF互相平分练一练(1)△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.AEDCB(1)(2) △ABC中,D、E分别是AB、AC的中点,∠A=50°, ∠B=70°,则∠AED=_____.练一练2、填空题5cm10560°50°70°60°60°(4)三角形的周长为18cm,面积为48cm2 ,这个三角形的三条中位线围成三角形的周长是 ,面积是 .(3)如图,E是平行四边形ABCD的AB边上的中点,且AD=10cm,那么OE= cm.5练一练2、填空题9cm10512cm2①图中有几个平行四边形?②图中有几个三角形?它们有什么关系?思考:(5)如图:如果AD= AB,AE= AC,
DE=2cm,那么BC= cm。ACDBE(6)在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是 。811练一练2、填空题248381.51.544四边形EFGH
是平行四边形吗?顺次连结四边形各边中点所得的四边形是平行四边形已知:E、F、G、H分别是四边形ABCD中AB、 BC、CD、DA的中点。
求证:EFGH是平行四边形。例2、求证:实践应用3、如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?ABC练一练求证:DE=EF挑战自我: 4.已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN。D,E,F分别是MB,BC,CN的中点,连结DE,EF。练一练1.三角形的中位线定义.2.三角形的中位线定理.3. 在三角形中给出一边的中点时,通常要转化为中位线来解题.4.线段的倍分要转化为相等问题来解决.5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)小结巩固新知
1.三角形的中位线_______第三边,并且______第三边的____________
2.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=——
3.若等腰△ABC的周长是40cm,AB=AC=14cm,则中位线DE=———60°4ABCDED 8cm6cm 平行于
等于 一半 4.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,
若MN =12 ,则BC = . 61°24 5. 如图, △ABC 中, D ,E 分别为AB,
AC 的中点,当BC =10㎝时,则DE = .5㎝ 6.如图,已知△ABC中,
AB = 3㎝,BC=3.4 ㎝ AC=4㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长
是 ㎝.
5.27、如下图:在Rt △ ABC中,∠A=90°,D、E、F分别是各边中点, AB=6cm,AC=8cm,则△DEF的周长= cm。12EFBACD
