2016-2017学年度冀教版八年级上学期数学期末模拟试题1
文档属性
| 名称 | 2016-2017学年度冀教版八年级上学期数学期末模拟试题1 |

|
|
| 格式 | zip | ||
| 文件大小 | 193.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-20 00:00:00 | ||
图片预览



文档简介
登陆21世纪教育 助您教考全无忧
2016-2017冀教版八年级上数学期末模拟试题1
班级___________姓名_________________总分__________________
一.选择题(共12小题)
1.下列各式中,分式的个数是( ).
A.2 B.3 C.4 D.5
2.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A.若甲对,则乙对 B.若乙对,则甲对
C.若乙错,则甲错 D.若甲错,则乙对
3.实数的平方根为( )
A.a B.±a C.± D.±
4.要使式子﹣有意义,字母x的取值必须满足( )
A.x≤ B.x≥﹣ C.x≥且x≠3 D.x≥
5.下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )
6.若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A.12 B.9 C.12或9 D.9或7
7.化简的结果是( )
A. B. C. D.y
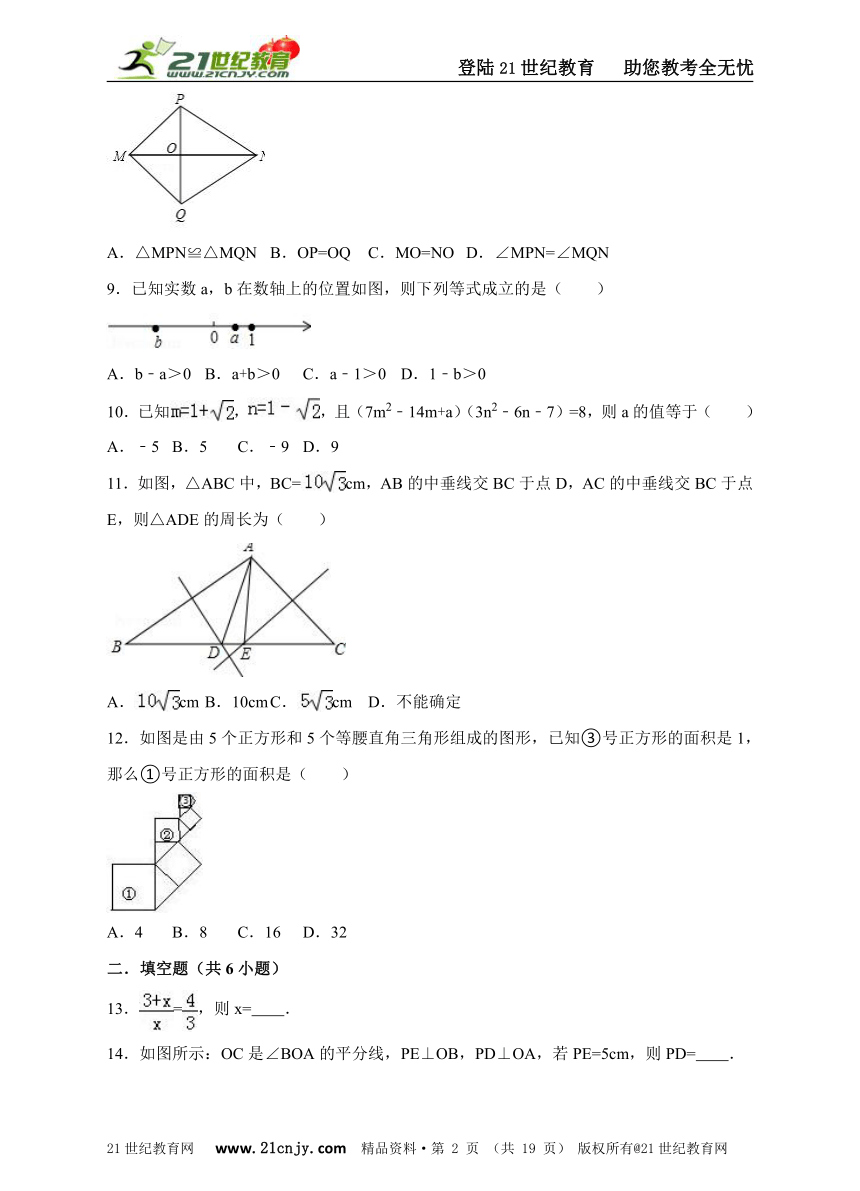
8.如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论中不正确的是( )
A.△MPN≌△MQN B.OP=OQ C.MO=NO D.∠MPN=∠MQN
9.已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
A.b﹣a>0 B.a+b>0 C.a﹣1>0 D.1﹣b>0
10.已知,,且(7m2﹣14m+a)(3n2﹣6n﹣7)=8,则a的值等于( )
A.﹣5 B.5 C.﹣9 D.9
11.如图,△ABC中,BC=cm,AB的中垂线交BC于点D,AC的中垂线交BC于点E,则△ADE的周长为( )
A.cm B.10cm C.cm D.不能确定
12.如图是由5个正方形和5个等腰直角三角形组成的图形,已知③号正方形的面积是1,那么①号正方形的面积是( )
A.4 B.8 C.16 D.32
二.填空题(共6小题)
13.=,则x= .
14.如图所示:OC是∠BOA的平分线,PE⊥OB,PD⊥OA,若PE=5cm,则PD= .
15.4.24970≈ (精确到百分位);近似数6.34万精确到 位.
16.方程(y﹣1)=y+1的解是 .
17.用反证法证明:“在同一平面内,若a垂直于b,b垂直于c,则a平行于c”,应假设 .
18.星光时代广场有一部自动扶梯匀速由下而上运动,甲、乙两人在乘扶梯的同时匀速登梯,甲登了30级后到达楼上,乙登梯的速度是甲的2倍(单位时间内乙登楼级数是甲的2倍),他登了36级后到达楼上,那么由楼下到楼上自动扶梯级数为 .
三.解答题(共8小题)
19.(1)计算:﹣(π﹣3)0+(﹣1)2013+|2﹣|;
(2)解方程:.
20.如图:AN⊥OB,BM⊥OA,垂足分别为N,M,OM=ON.
求证:PM=PN.
21.(1)先化简、再求值:,其中x=,y=3.
(2)先化简、再求值:,其中a=.
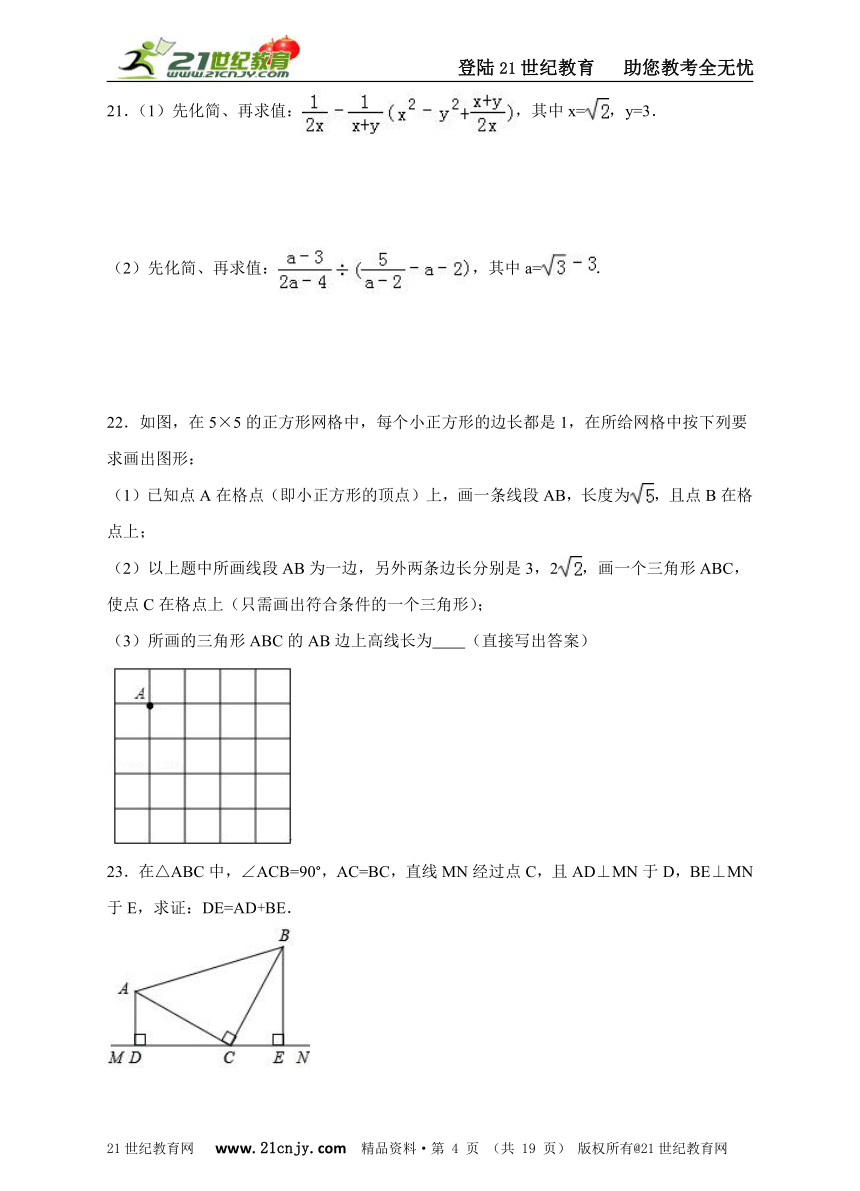
22.如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:
(1)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为,且点B在格点上;
(2)以上题中所画线段AB为一边,另外两条边长分别是3,2,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);
(3)所画的三角形ABC的AB边上高线长为 (直接写出答案)
23.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.
24.某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
25.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为:…①(其中a、b、c为三角形的三边长,s为面积).
而另一个文明古国古希腊也有求三角形面积的海伦公式:
s=…②(其中p=.)
(1)若已知三角形的三边长分别为5,7,8,试分别运用公式①和公式②,计算该三角形的面积s;
(2)你能否由公式①推导出公式②?请试试.
26.探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
参考答案与试题解析
一.选择题(共12小题)
1. 分析:判断分式的依据是看代数式的分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
解:,的分母中均不含有字母,因此它们是整式,而不是分式;
a+的分子不是整式,因此不是分式.
,,的分母中含有字母,因此是分式.
故选:B.
2. 分析:分别假设甲说的对和乙说的正确,进而得出答案.
解:若甲对,即只参加一项的人数大于14人,不妨假设只参加一项的人数是15人,
则两项都参加的人数为5人,故乙错.
若乙对,即两项都参加的人数小于5人,则两项都参加的人数至多为4人,
此时只参加一项的人数为16人,故甲对.
故选:B.
3. 分析:首先根据算术平方根的定义可以求得=|a|,再利用绝对值的定义可以化简|a|即可得到结果.
解:∵当a为任意实数时,=|a|,
而|a|的平方根为.
∴实数的平方根为.
故选:D.
4. 分析:根据二次根式有意义的条件可得2x﹣3≥0,根据分式有意义的条件可得x﹣3≠0,再解即可.
解:由题意得:2x﹣3≥0,且x﹣3≠0,
解得:x≥,且x≠3,
故选:C.
5. 分析:根据轴对称图形的概念求解.
解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选D.
6. 分析:利用等腰三角形的性质以及三角形三边关系得出其周长即可.
解:∵一个等腰三角形的两边长分别是2和5,
∴当腰长为2,则2+2<5,此时不成立,
当腰长为5时,则它的周长为:5+5+2=12.
故选:A.
7. 分析:首先利用分式的加减运算法则计算括号里面的,然后再利用分式的乘除运算法则求得结果.
解:= = =.
故选B.
8. 分析:由已知条件中两边对应相等加上公共边很容易得到△MPN≌△MQN,可得∠MPN=∠MQN,进而可得△PON≌△QON可得OP=OQ
于是答案可得.
解:∵MP=MQ,PN=QN,MN=MN,
∴△MPN≌△MQN
故A正确;
∵MN垂直平分PQ
∴OP=OQ
故B正确;
∴∠MPN=∠MQN
故D正确.
∴只有C是错误的.
故选C.
9. 分析:本题运用实数与数轴的对应关系确定b<0,1>a>0,且|b|>1>|a|,然后根据绝对值的意义化简即可求解.
解:由数轴上a,b两点的位置可知b<0,1>a>0,且|b|>|a|,
A、b﹣a<0,故选项A错误;
B、|a+b<0,故选项B错误;
C、a﹣1<0,故选项C错误;
D、|正确.
故选:D.
10. 分析:观察已知等式可知,两个括号里分别有m2﹣2m,n2﹣2n的结构,可由已知m、n的值移项,平方得出m2﹣2m,n2﹣2n的值,代入已知等式即可.
解:由m=1+得m﹣1=,
两边平方,得m2﹣2m+1=2
即m2﹣2m=1,同理得n2﹣2n=1.
又(7m2﹣14m+a)(3n2﹣6n﹣7)=8,
所以(7+a)(3﹣7)=8,
解得a=﹣9
故选C.
11. 分析:先根据线段垂直平分线的性质求出AD=BD,AE=CE,再通过等量代换即可得出答案.
解:∵AB的中垂线交BC于点D,AC的中垂线交BC于点E,
∴AD=BD,AE=CE,
∴BC=BD+CE+DE=AD+AC+DE=10cm.
故选A.
12. 分析:等腰直角三角形中,直角边长和斜边长的比值为1:,正方形面积为边长的平方;
所以要求①号正方形的面积,求出①号正方形的边长即可.
解:
要求①号正方形的面积,求①号正方形的边长即可,
题目中给出③号正方形的面积为1,即③号正方形的边长为1,
根据勾股定理4号正方形的边长为=,
以此类推,可以求得①号正方形边长为4,
所以①号正方形面积为4×4=16.
故选C.
二.填空题(共6小题)
13. 分析:首先两边同时乘以3x去分母可得3(3+x)=4x,再解整式方程可得x的值,然后进行检验即可.
解:两边同时乘以3x得:3(3+x)=4x,
解得:x=9,
检验:把x=9代入最简公分母3x≠0,
则x=9是分式方程的解,
故答案为:9.
14. 分析:根据角平分线性质得出PE=PD,代入求出即可.
解:∵OC是∠BOA的平分线,PE⊥OB,PD⊥OA,
∴PE=PD,
∵PE=5cm,
∴PD=5cm,
故答案为:5cm.
15. 分析:把数4.24970的千分位上的数字9进行四舍五入得到4.24970≈4.25;近似数6.34万精确到0.01万位.
解:4.24970≈4.25(精确到百分位);近似数6.34万精确到百位.
故答案为4.25;百.
16. 分析:先去括号,再移项,合并同类项,系数化1,再进行整理即可.
解:∵(y﹣1)=y+1,
∴y﹣﹣y=1,
∴(﹣1)y=1+
∴y=,
∴y=3+2;
故答案为:y=3+2.
17. 分析:反证法的步骤中,第一步是假设结论不成立,反面成立,可据即可解答.
解:用反证法证明“在同一平面内,若a⊥b,b⊥c,则a∥b”,应假设:a不平行b或a与b相交.
故答案是:a不平行b或a与b相交.
18. 分析:可以设自动扶梯在单位时间上升x级,甲在单位时间上y级,则乙在单位时间上2y级,由甲上的台阶总数为x+y,需要的时间为30÷y,即可得总扶梯阶数;同理可根据甲的登梯情况列出乙登梯的代数式,由扶梯从楼下到楼上的级数相等建立方程,解方程可得x与y的关系,代入其中一个代数式即可得扶梯阶数.
解:设自动扶梯在单位时间上升x级,甲在单位时间上y级,则乙在单位时间上2y级.根据题意得:
(x+y)×=(x+2y)×,
解得:y=2x.
即甲上2级,自动扶梯上升1级,
那么由楼下到楼上,自动扶梯级数为:(x+y)×=
+30=45(级).
故答案为:45级.
三.解答题(共8小题)
19. 分析:(1)原式第一项利用立方根的定义化简,第二项利用零指数幂法则计算,第三项利用﹣1的奇次幂为﹣1,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:(1)原式=2﹣1+(﹣1)+2﹣
=2﹣;
(2)方程两边同乘(2x+1),得:4=x+2x+1,
解得:x=1,
检验:把x=1代入2x+1=3≠0,
故原分式方程的解为x=1.
20. 分析:首先证明△BOM≌△AON可得BO=AO,∠A=∠B,进而得到BN=AM,再证明△BNP≌△AMP可得PM=PN.
证明:∵AN⊥OB,BM⊥OA,
∴∠ONA=∠OMB=90°,
在△OBM和△OAN中,
,
∴△BOM≌△AON(ASA),
∴BO=AO,∠A=∠B,
∴BO﹣ON=AO﹣OM,
即BN=AM,
在△BNP和△AMP中,
,
∴△BNP≌△AMP(AAS),
∴PM=PN.
21. 分析:(1)用平方差公式把(x2﹣y2)分解因式后,又分配律化简,再代值计算;
(2)先通分,变除法为乘法后,化简求值.
解:(1)原式=
=
=﹣(x﹣y)
=y﹣x,
当x=,y=3时,
原式=3;
(2)原式=
=
=
=,
当a=﹣3时,原式=﹣=﹣.
22. 分析:(1)根据勾股定理可知使线段AB为直角边为2和1的直角三角形的斜边即可;
(2)作出另外两条边长分别是3,2的三角形ABC即可;
(3)根据三角形的面积公式即可得到所画的三角形ABC的AB边上高线长.
解:(1)如图所示:
(2)如图所示:
(3)三角形ABC的AB边上高线长为:×3×2×2÷
=3×2÷
=.
故答案为:.
23. 分析:先证明∠BCE=∠CAD,再证明△ADC≌△CEB,可得到AD=CE,DC=EB,等量代换,可得出DE=AD+BE.
证明:∵∠ACB=90°,AC=BC,
∴∠ACD+∠BCE=90°,
又∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,而∠ACD+∠DAC=90°,
∴∠BCE=∠CAD.
在△ADC和△CEB中
∵,
∴△ADC≌△CEB(AAS).
∴AD=CE,DC=EB.
又∵DE=DC+CE,
∴DE=EB+AD.
24. 分析:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元.根据第二次购进干果数量是第一次的2倍还多300千克,列出方程,解方程即可求解;
(2)根据利润=售价﹣进价,可求出结果.
解:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元,
由题意,得=2×+300,
解得x=5,
经检验x=5是方程的解.
答:该种干果的第一次进价是每千克5元;
(2)[+﹣600]×9+600×9×80%﹣(3000+9000)
=(600+1500﹣600)×9+4320﹣12000
=1500×9+4320﹣12000
=13500+4320﹣12000
=5820(元).
答:超市销售这种干果共盈利5820元.
25. 分析:(1)代入计算即可;
(2)需要在括号内都乘以4,括号外再乘,保持等式不变,构成完全平方公式,再进行计算.
解:(1)s=,
=;
p=(5+7+8)=10,
又s=;
(2)=(﹣)
=,
=(c+a﹣b)(c﹣a+b)(a+b+c)(a+b﹣c),
=(2p﹣2a)(2p﹣2b) 2p (2p﹣2c),
=p(p﹣a)(p﹣b)(p﹣c),
∴=.
(说明:若在整个推导过程中,始终带根号运算当然也正确)
26. 分析:(1)利用直角三角形的性质“直角三角形斜边中线等于斜边的一半”得到DE=DF;
(2)利用等腰三角形的性质和判定得出结论,从而判定△MEB≌△MFA(AAS),得到DE=DF.
(3)利用三角形的中位线和直角三角形的性质根据SAS证明△DHE≌△FGD可得.
解:(1)∵AE⊥BC,BF⊥AC
∴△AEB和△AFB都是直角三角形
∵D是AB的中点
∴DE和DF分别为Rt△AEB和Rt△AFB的斜边中线
∴DE=AB,DF=AB(直角三角形斜边中线等于斜边的一半)
∴DE=DF
∵DE=kDF
∴k=1
(2)∵CB=CA
∴∠CBA=∠CAB
∵∠MAC=∠MB
∴∠CBA﹣∠MBC=∠CAB﹣∠MAC
即∠ABM=∠BAM
∴AM=BM
∵ME⊥BC,MF⊥AC
∴∠MEB=∠MFA=90
又∵∠MBE=∠MAF
∴△MEB≌△MFA(AAS)
∴BE=AF
∵D是AB的中点,即BD=AD
又∵∠DBE=∠DAF
∴△DBE≌△DAF(SAS)
∴DE=DF
(3)DE=DF
如图1,作AM的中点G,BM的中点H,
∵点 D是 边 AB的 中点
∴DG∥BM,DG=BM
同理可得:DH∥AM,DH=AM
∵ME⊥BC于E,H 是BM的中点
∴在Rt△BEM中,HE=BM=BH
∴∠HBE=∠HEB
∠MHE=∠HBE+∠HEB=2∠MBC
又∵DG=BM,HE=BM
∴DG=HE
同理可得:DH=FG,∠MGF=2∠MAC
∵DG∥BM,DH∥GM
∴四边形DHMG是平行四边形
∴∠DGM=∠DHM
∵∠MGF=2∠MAC,∠MHE=2∠MBC
又∵∠MBC=∠MAC
∴∠MGF=∠MHE
∴∠DGM+∠MGF=∠DHM+∠MHE
∴∠DGF=∠DHE
在△DHE与△FGD中
,
∴△DHE≌△FGD(SAS),
∴DE=DF
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 19 页) 版权所有@21世纪教育网
2016-2017冀教版八年级上数学期末模拟试题1
班级___________姓名_________________总分__________________
一.选择题(共12小题)
1.下列各式中,分式的个数是( ).
A.2 B.3 C.4 D.5
2.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A.若甲对,则乙对 B.若乙对,则甲对
C.若乙错,则甲错 D.若甲错,则乙对
3.实数的平方根为( )
A.a B.±a C.± D.±
4.要使式子﹣有意义,字母x的取值必须满足( )
A.x≤ B.x≥﹣ C.x≥且x≠3 D.x≥
5.下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )
6.若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A.12 B.9 C.12或9 D.9或7
7.化简的结果是( )
A. B. C. D.y
8.如图,MP=MQ,PN=QN,MN交PQ于点O,则下列结论中不正确的是( )
A.△MPN≌△MQN B.OP=OQ C.MO=NO D.∠MPN=∠MQN
9.已知实数a,b在数轴上的位置如图,则下列等式成立的是( )
A.b﹣a>0 B.a+b>0 C.a﹣1>0 D.1﹣b>0
10.已知,,且(7m2﹣14m+a)(3n2﹣6n﹣7)=8,则a的值等于( )
A.﹣5 B.5 C.﹣9 D.9
11.如图,△ABC中,BC=cm,AB的中垂线交BC于点D,AC的中垂线交BC于点E,则△ADE的周长为( )
A.cm B.10cm C.cm D.不能确定
12.如图是由5个正方形和5个等腰直角三角形组成的图形,已知③号正方形的面积是1,那么①号正方形的面积是( )
A.4 B.8 C.16 D.32
二.填空题(共6小题)
13.=,则x= .
14.如图所示:OC是∠BOA的平分线,PE⊥OB,PD⊥OA,若PE=5cm,则PD= .
15.4.24970≈ (精确到百分位);近似数6.34万精确到 位.
16.方程(y﹣1)=y+1的解是 .
17.用反证法证明:“在同一平面内,若a垂直于b,b垂直于c,则a平行于c”,应假设 .
18.星光时代广场有一部自动扶梯匀速由下而上运动,甲、乙两人在乘扶梯的同时匀速登梯,甲登了30级后到达楼上,乙登梯的速度是甲的2倍(单位时间内乙登楼级数是甲的2倍),他登了36级后到达楼上,那么由楼下到楼上自动扶梯级数为 .
三.解答题(共8小题)
19.(1)计算:﹣(π﹣3)0+(﹣1)2013+|2﹣|;
(2)解方程:.
20.如图:AN⊥OB,BM⊥OA,垂足分别为N,M,OM=ON.
求证:PM=PN.
21.(1)先化简、再求值:,其中x=,y=3.
(2)先化简、再求值:,其中a=.
22.如图,在5×5的正方形网格中,每个小正方形的边长都是1,在所给网格中按下列要求画出图形:
(1)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为,且点B在格点上;
(2)以上题中所画线段AB为一边,另外两条边长分别是3,2,画一个三角形ABC,使点C在格点上(只需画出符合条件的一个三角形);
(3)所画的三角形ABC的AB边上高线长为 (直接写出答案)
23.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.
24.某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
25.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为:…①(其中a、b、c为三角形的三边长,s为面积).
而另一个文明古国古希腊也有求三角形面积的海伦公式:
s=…②(其中p=.)
(1)若已知三角形的三边长分别为5,7,8,试分别运用公式①和公式②,计算该三角形的面积s;
(2)你能否由公式①推导出公式②?请试试.
26.探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
参考答案与试题解析
一.选择题(共12小题)
1. 分析:判断分式的依据是看代数式的分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
解:,的分母中均不含有字母,因此它们是整式,而不是分式;
a+的分子不是整式,因此不是分式.
,,的分母中含有字母,因此是分式.
故选:B.
2. 分析:分别假设甲说的对和乙说的正确,进而得出答案.
解:若甲对,即只参加一项的人数大于14人,不妨假设只参加一项的人数是15人,
则两项都参加的人数为5人,故乙错.
若乙对,即两项都参加的人数小于5人,则两项都参加的人数至多为4人,
此时只参加一项的人数为16人,故甲对.
故选:B.
3. 分析:首先根据算术平方根的定义可以求得=|a|,再利用绝对值的定义可以化简|a|即可得到结果.
解:∵当a为任意实数时,=|a|,
而|a|的平方根为.
∴实数的平方根为.
故选:D.
4. 分析:根据二次根式有意义的条件可得2x﹣3≥0,根据分式有意义的条件可得x﹣3≠0,再解即可.
解:由题意得:2x﹣3≥0,且x﹣3≠0,
解得:x≥,且x≠3,
故选:C.
5. 分析:根据轴对称图形的概念求解.
解:A、不是轴对称图形,故本选项错误;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、是轴对称图形,故本选项正确.
故选D.
6. 分析:利用等腰三角形的性质以及三角形三边关系得出其周长即可.
解:∵一个等腰三角形的两边长分别是2和5,
∴当腰长为2,则2+2<5,此时不成立,
当腰长为5时,则它的周长为:5+5+2=12.
故选:A.
7. 分析:首先利用分式的加减运算法则计算括号里面的,然后再利用分式的乘除运算法则求得结果.
解:= = =.
故选B.
8. 分析:由已知条件中两边对应相等加上公共边很容易得到△MPN≌△MQN,可得∠MPN=∠MQN,进而可得△PON≌△QON可得OP=OQ
于是答案可得.
解:∵MP=MQ,PN=QN,MN=MN,
∴△MPN≌△MQN
故A正确;
∵MN垂直平分PQ
∴OP=OQ
故B正确;
∴∠MPN=∠MQN
故D正确.
∴只有C是错误的.
故选C.
9. 分析:本题运用实数与数轴的对应关系确定b<0,1>a>0,且|b|>1>|a|,然后根据绝对值的意义化简即可求解.
解:由数轴上a,b两点的位置可知b<0,1>a>0,且|b|>|a|,
A、b﹣a<0,故选项A错误;
B、|a+b<0,故选项B错误;
C、a﹣1<0,故选项C错误;
D、|正确.
故选:D.
10. 分析:观察已知等式可知,两个括号里分别有m2﹣2m,n2﹣2n的结构,可由已知m、n的值移项,平方得出m2﹣2m,n2﹣2n的值,代入已知等式即可.
解:由m=1+得m﹣1=,
两边平方,得m2﹣2m+1=2
即m2﹣2m=1,同理得n2﹣2n=1.
又(7m2﹣14m+a)(3n2﹣6n﹣7)=8,
所以(7+a)(3﹣7)=8,
解得a=﹣9
故选C.
11. 分析:先根据线段垂直平分线的性质求出AD=BD,AE=CE,再通过等量代换即可得出答案.
解:∵AB的中垂线交BC于点D,AC的中垂线交BC于点E,
∴AD=BD,AE=CE,
∴BC=BD+CE+DE=AD+AC+DE=10cm.
故选A.
12. 分析:等腰直角三角形中,直角边长和斜边长的比值为1:,正方形面积为边长的平方;
所以要求①号正方形的面积,求出①号正方形的边长即可.
解:
要求①号正方形的面积,求①号正方形的边长即可,
题目中给出③号正方形的面积为1,即③号正方形的边长为1,
根据勾股定理4号正方形的边长为=,
以此类推,可以求得①号正方形边长为4,
所以①号正方形面积为4×4=16.
故选C.
二.填空题(共6小题)
13. 分析:首先两边同时乘以3x去分母可得3(3+x)=4x,再解整式方程可得x的值,然后进行检验即可.
解:两边同时乘以3x得:3(3+x)=4x,
解得:x=9,
检验:把x=9代入最简公分母3x≠0,
则x=9是分式方程的解,
故答案为:9.
14. 分析:根据角平分线性质得出PE=PD,代入求出即可.
解:∵OC是∠BOA的平分线,PE⊥OB,PD⊥OA,
∴PE=PD,
∵PE=5cm,
∴PD=5cm,
故答案为:5cm.
15. 分析:把数4.24970的千分位上的数字9进行四舍五入得到4.24970≈4.25;近似数6.34万精确到0.01万位.
解:4.24970≈4.25(精确到百分位);近似数6.34万精确到百位.
故答案为4.25;百.
16. 分析:先去括号,再移项,合并同类项,系数化1,再进行整理即可.
解:∵(y﹣1)=y+1,
∴y﹣﹣y=1,
∴(﹣1)y=1+
∴y=,
∴y=3+2;
故答案为:y=3+2.
17. 分析:反证法的步骤中,第一步是假设结论不成立,反面成立,可据即可解答.
解:用反证法证明“在同一平面内,若a⊥b,b⊥c,则a∥b”,应假设:a不平行b或a与b相交.
故答案是:a不平行b或a与b相交.
18. 分析:可以设自动扶梯在单位时间上升x级,甲在单位时间上y级,则乙在单位时间上2y级,由甲上的台阶总数为x+y,需要的时间为30÷y,即可得总扶梯阶数;同理可根据甲的登梯情况列出乙登梯的代数式,由扶梯从楼下到楼上的级数相等建立方程,解方程可得x与y的关系,代入其中一个代数式即可得扶梯阶数.
解:设自动扶梯在单位时间上升x级,甲在单位时间上y级,则乙在单位时间上2y级.根据题意得:
(x+y)×=(x+2y)×,
解得:y=2x.
即甲上2级,自动扶梯上升1级,
那么由楼下到楼上,自动扶梯级数为:(x+y)×=
+30=45(级).
故答案为:45级.
三.解答题(共8小题)
19. 分析:(1)原式第一项利用立方根的定义化简,第二项利用零指数幂法则计算,第三项利用﹣1的奇次幂为﹣1,最后一项利用绝对值的代数意义化简,计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:(1)原式=2﹣1+(﹣1)+2﹣
=2﹣;
(2)方程两边同乘(2x+1),得:4=x+2x+1,
解得:x=1,
检验:把x=1代入2x+1=3≠0,
故原分式方程的解为x=1.
20. 分析:首先证明△BOM≌△AON可得BO=AO,∠A=∠B,进而得到BN=AM,再证明△BNP≌△AMP可得PM=PN.
证明:∵AN⊥OB,BM⊥OA,
∴∠ONA=∠OMB=90°,
在△OBM和△OAN中,
,
∴△BOM≌△AON(ASA),
∴BO=AO,∠A=∠B,
∴BO﹣ON=AO﹣OM,
即BN=AM,
在△BNP和△AMP中,
,
∴△BNP≌△AMP(AAS),
∴PM=PN.
21. 分析:(1)用平方差公式把(x2﹣y2)分解因式后,又分配律化简,再代值计算;
(2)先通分,变除法为乘法后,化简求值.
解:(1)原式=
=
=﹣(x﹣y)
=y﹣x,
当x=,y=3时,
原式=3;
(2)原式=
=
=
=,
当a=﹣3时,原式=﹣=﹣.
22. 分析:(1)根据勾股定理可知使线段AB为直角边为2和1的直角三角形的斜边即可;
(2)作出另外两条边长分别是3,2的三角形ABC即可;
(3)根据三角形的面积公式即可得到所画的三角形ABC的AB边上高线长.
解:(1)如图所示:
(2)如图所示:
(3)三角形ABC的AB边上高线长为:×3×2×2÷
=3×2÷
=.
故答案为:.
23. 分析:先证明∠BCE=∠CAD,再证明△ADC≌△CEB,可得到AD=CE,DC=EB,等量代换,可得出DE=AD+BE.
证明:∵∠ACB=90°,AC=BC,
∴∠ACD+∠BCE=90°,
又∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,而∠ACD+∠DAC=90°,
∴∠BCE=∠CAD.
在△ADC和△CEB中
∵,
∴△ADC≌△CEB(AAS).
∴AD=CE,DC=EB.
又∵DE=DC+CE,
∴DE=EB+AD.
24. 分析:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元.根据第二次购进干果数量是第一次的2倍还多300千克,列出方程,解方程即可求解;
(2)根据利润=售价﹣进价,可求出结果.
解:(1)设该种干果的第一次进价是每千克x元,则第二次进价是每千克(1+20%)x元,
由题意,得=2×+300,
解得x=5,
经检验x=5是方程的解.
答:该种干果的第一次进价是每千克5元;
(2)[+﹣600]×9+600×9×80%﹣(3000+9000)
=(600+1500﹣600)×9+4320﹣12000
=1500×9+4320﹣12000
=13500+4320﹣12000
=5820(元).
答:超市销售这种干果共盈利5820元.
25. 分析:(1)代入计算即可;
(2)需要在括号内都乘以4,括号外再乘,保持等式不变,构成完全平方公式,再进行计算.
解:(1)s=,
=;
p=(5+7+8)=10,
又s=;
(2)=(﹣)
=,
=(c+a﹣b)(c﹣a+b)(a+b+c)(a+b﹣c),
=(2p﹣2a)(2p﹣2b) 2p (2p﹣2c),
=p(p﹣a)(p﹣b)(p﹣c),
∴=.
(说明:若在整个推导过程中,始终带根号运算当然也正确)
26. 分析:(1)利用直角三角形的性质“直角三角形斜边中线等于斜边的一半”得到DE=DF;
(2)利用等腰三角形的性质和判定得出结论,从而判定△MEB≌△MFA(AAS),得到DE=DF.
(3)利用三角形的中位线和直角三角形的性质根据SAS证明△DHE≌△FGD可得.
解:(1)∵AE⊥BC,BF⊥AC
∴△AEB和△AFB都是直角三角形
∵D是AB的中点
∴DE和DF分别为Rt△AEB和Rt△AFB的斜边中线
∴DE=AB,DF=AB(直角三角形斜边中线等于斜边的一半)
∴DE=DF
∵DE=kDF
∴k=1
(2)∵CB=CA
∴∠CBA=∠CAB
∵∠MAC=∠MB
∴∠CBA﹣∠MBC=∠CAB﹣∠MAC
即∠ABM=∠BAM
∴AM=BM
∵ME⊥BC,MF⊥AC
∴∠MEB=∠MFA=90
又∵∠MBE=∠MAF
∴△MEB≌△MFA(AAS)
∴BE=AF
∵D是AB的中点,即BD=AD
又∵∠DBE=∠DAF
∴△DBE≌△DAF(SAS)
∴DE=DF
(3)DE=DF
如图1,作AM的中点G,BM的中点H,
∵点 D是 边 AB的 中点
∴DG∥BM,DG=BM
同理可得:DH∥AM,DH=AM
∵ME⊥BC于E,H 是BM的中点
∴在Rt△BEM中,HE=BM=BH
∴∠HBE=∠HEB
∠MHE=∠HBE+∠HEB=2∠MBC
又∵DG=BM,HE=BM
∴DG=HE
同理可得:DH=FG,∠MGF=2∠MAC
∵DG∥BM,DH∥GM
∴四边形DHMG是平行四边形
∴∠DGM=∠DHM
∵∠MGF=2∠MAC,∠MHE=2∠MBC
又∵∠MBC=∠MAC
∴∠MGF=∠MHE
∴∠DGM+∠MGF=∠DHM+∠MHE
∴∠DGF=∠DHE
在△DHE与△FGD中
,
∴△DHE≌△FGD(SAS),
∴DE=DF
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 (共 19 页) 版权所有@21世纪教育网
同课章节目录
