面面垂直的性质_讲课

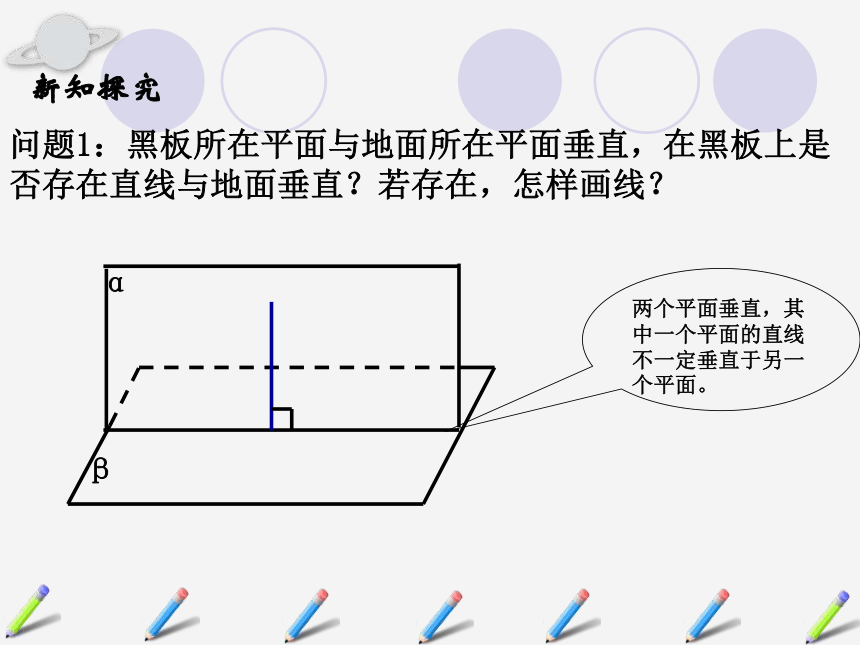
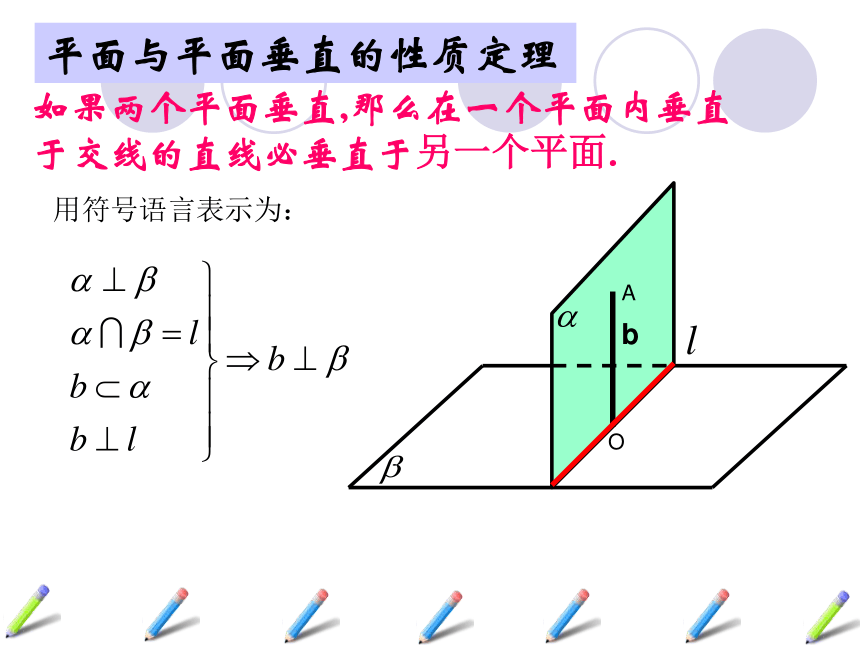
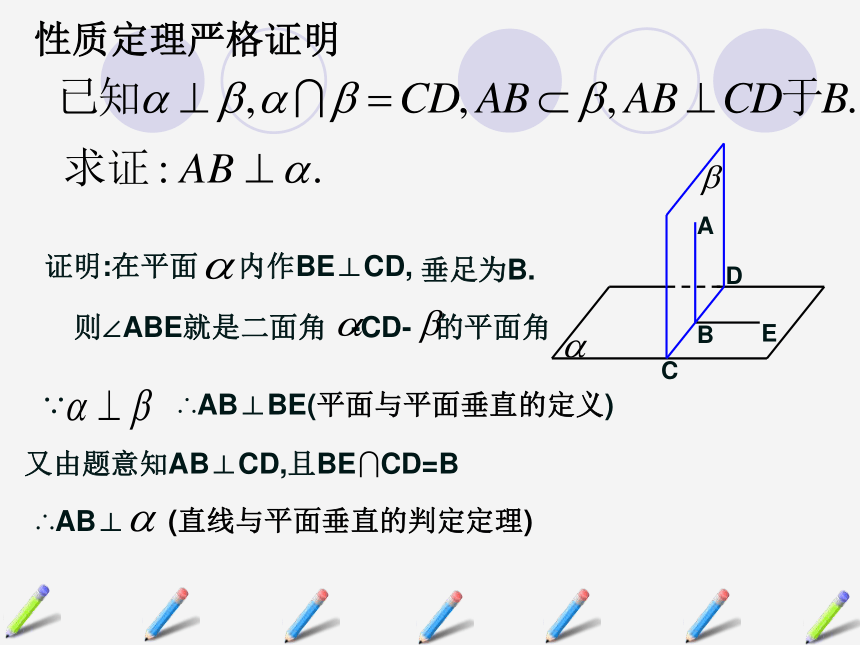
课件17张PPT。2.3.4平面与平面垂直的性质复习引入1、平面与平面垂直的定义2、平面与平面垂直的判定定理线面垂直 面面垂直 反过来，在平面与平面垂直的条件下能否得到线面垂直呢？两个平面相交，如果它们所成的二面角是直二面角，则两个平面垂直.若一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.新知探究 问题1：黑板所在平面与地面所在平面垂直，在黑板上是否存在直线与地面垂直？若存在，怎样画线？两个平面垂直，其中一个平面的直线不一定垂直于另一个平面。两个平面垂直，其中一个平面内垂直于交线的直线垂直于另一个平面。概括结论如果两个平面垂直,那么在一个平面内垂直于交线的直线必垂直于另一个平面.平面与平面垂直的性质定理用符号语言表示为：则∠ABE就是二面角 -CD- 的平面角∵ ∴AB⊥BE(平面与平面垂直的定义)又由题意知AB⊥CD,且BE CD=BEDC性质定理严格证明定理剖析：1、面面垂直?线面垂直；（线是一个平面内垂直于两平面交线的一条直线）αβAB2、可作为线面垂直的判定定理；3、为作面的垂线提供依据和方法.新知探究思考：平面?⊥平面β，结论：直线PC在平面?内说明:这个结论是面面垂直的另一个性质，如果两个平面垂直，那么经过第一个平面内的一点垂直于第二个平面的直线，在第一个平面内.文字语言：PCABD√××ι(4) 过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面。×应用巩固例2：如图:已知平面 ,直线 满足
试判断直线 与平面 的位置关系.解:在 内作垂直于 与 交线的直线∵∵即直线 与平面 平行.又∵应用巩固αβAbalB垂直乘胜追击
例3：如图，AB是⊙O的直径，C是圆周上不同于A，B的任意一点，平面PAC⊥平面ABC.(2)判断平面PBC与平面PAC的位置关系。(1)判断BC与平面PAC的位置关系，并证明。 (1)证明：∵ AB是⊙O的直径，C是圆周上不 同于A，B的任意一点 ∴∠ACB=90°
∴BC⊥AC 又∵平面PAC⊥平面ABC，
平面PAC∩平面ABC＝AC, BC 平面ABC ∴BC⊥平面PAC(2)又∵ BC 平面PBC ，∴平面PBC⊥平面PAC 1．给出下列四个命题：　　①垂直于同一个平面的两个平面平行；　　②垂直于同一条直线的两个平面平行；　　③垂直于同一个平面的两条直线平行；　　④垂直于同一条直线的两条直线平行．其中正确的命题的个数是（????? ）．　　A．1???????? B．2?????????? C．3?????????? D．4巩固深化 发展思维B? 2．给出下列四个命题：（其中a，b表直线，α，β, γ表平面）。　　①若a⊥b，a∥α，则b⊥α；　　②若a∥α，α⊥β，则a⊥β；　　③若β∥γ，α∥γ，则α⊥β；　　④若α⊥β，a⊥β，则a∥α。其中不正确的命题的个数是（????? ）．　　A．1???????? B．2??????????? C．3????????? D．4D一、平面与平面垂直的性质定理：
定理1：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。
定理2：两个平面垂直，那么经过第一个平面内的一点垂直于第二个平面的直线，必在第一个平面内.归纳总结二、空间垂直关系有线线垂直、线面垂直、面面垂直，请指出空间垂直关系相互转化的依据？①线面垂直的判定定理 ②线面垂直的定义 ③面面垂直的判定定理 ④面面垂直的性质定理 必做题:
课本73页习题2.3A组第2、5题选做题:
74页B组第3,4题布置作业谢谢指导