二次函数在闭区间上的最值
图片预览


文档简介
课件8张PPT。 二次函数在闭区间上的最值彭阳县第三中学
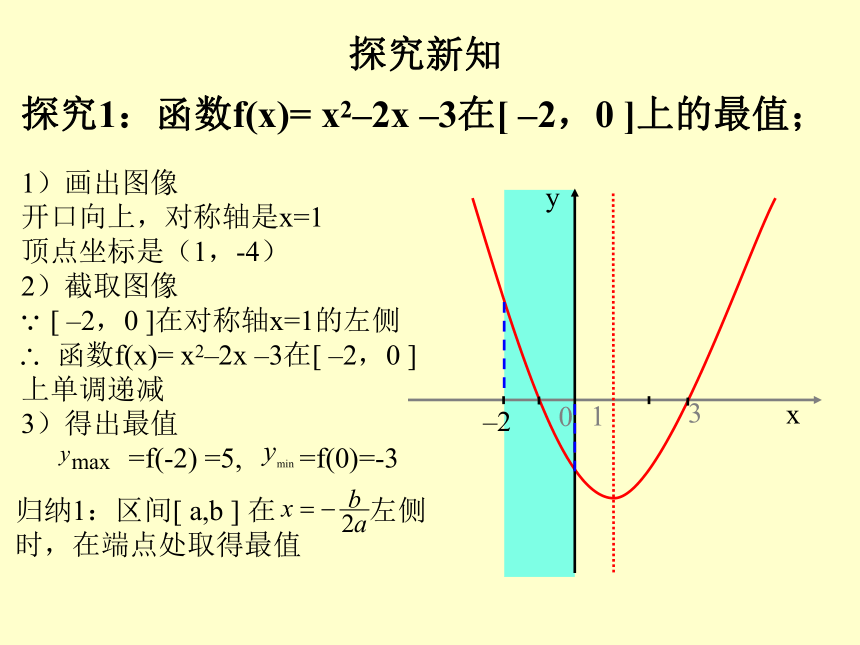
人民教育出版社必修一二次函数 y= ax2+bx+c的图象和性质RR知识衔接先减后增先增后减探究1:函数f(x)= x2–2x –3在[ –2,0 ]上的最值;
1)画出图像
开口向上,对称轴是x=1
顶点坐标是(1,-4)
2)截取图像
[ –2,0 ]在对称轴x=1的左侧
函数f(x)= x2–2x –3在[ –2,0 ]
上单调递减
3)得出最值
=f(-2) =5, =f(0)=-3归纳1:区间[ a,b ] 在 左侧
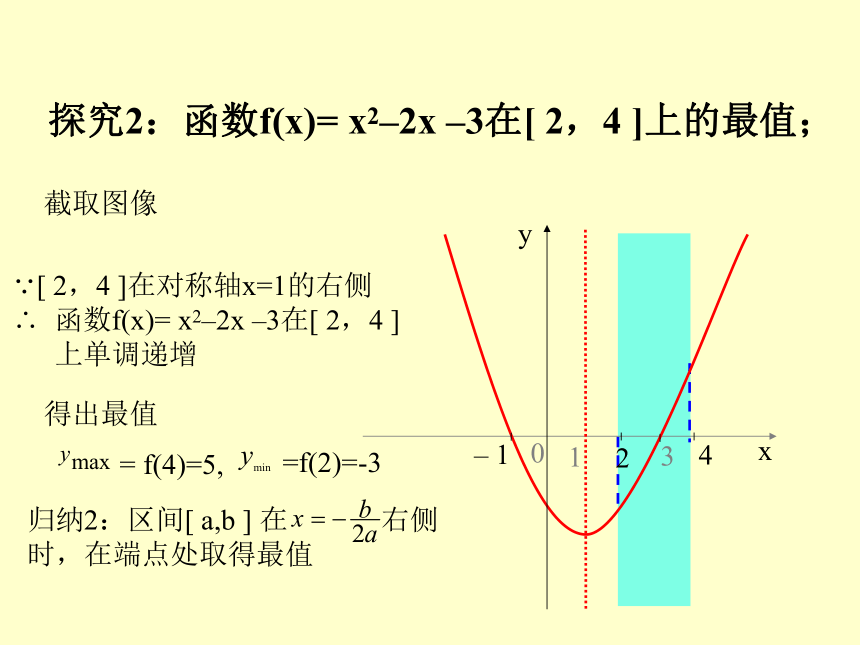
时,在端点处取得最值探究新知探究2:函数f(x)= x2–2x –3在[ 2,4 ]上的最值;
截取图像[ 2,4 ]在对称轴x=1的右侧
得出最值
归纳2:区间[ a,b ] 在 右侧
时,在端点处取得最值= f(4)=5,=f(2)=-3函数f(x)= x2–2x –3在[ 2,4 ]
上单调递增
探究3:函数f(x)= x2–2x –3在[ ]上的最值;截取图像对称轴x=1在[ ]内
函数f(x)= x2–2x –3在[ ]上先减后增得出最值
f( )= ,f(1)=-4 ,f( )=
= , =-4归纳3:对称轴 在区间[ a,b ] 内时,在端点或顶点处取得最值方法总结:求二次函数f(x)=ax2+bx+c在[m,n]上的最值: 方法一:
(1)画出图像(2)截取图像(3)得出最值
数形结合方法二:
(1)检查x0= 是否属于 [ m,n];
(2)当x0∈[m,n]时,f(m)、f(n)、f(x0)中的较大者是最大值,较小者是最小值;
(3)当x0 [m,n]时,f(m)、f(n)中的较大者是最大值,较小者是最小值.练习:求二次函数f(x)=x2-2ax-3在闭区间[3,4]上的最小值。解:如图可得:
1°当a<3时二次函数在[3,4]上单调递增
∴ f(x)min=f(3)=6-6a3°当a>4时,二次函数在[3,4]上单调递减∴ f(x)min=f(4)=13-8a
小结:求二次函数闭区间上的最值,含有参数时要分情况讨论,一般分对称轴在区间的左、中、右三种情况进行讨论yxo342°当3 a 4时二次函数先减后增
∴ f(x)min=f(a)=-a2-3学以致用谢谢各位光临指导
人民教育出版社必修一二次函数 y= ax2+bx+c的图象和性质RR知识衔接先减后增先增后减探究1:函数f(x)= x2–2x –3在[ –2,0 ]上的最值;
1)画出图像
开口向上,对称轴是x=1
顶点坐标是(1,-4)
2)截取图像
[ –2,0 ]在对称轴x=1的左侧
函数f(x)= x2–2x –3在[ –2,0 ]
上单调递减
3)得出最值
=f(-2) =5, =f(0)=-3归纳1:区间[ a,b ] 在 左侧
时,在端点处取得最值探究新知探究2:函数f(x)= x2–2x –3在[ 2,4 ]上的最值;
截取图像[ 2,4 ]在对称轴x=1的右侧
得出最值
归纳2:区间[ a,b ] 在 右侧
时,在端点处取得最值= f(4)=5,=f(2)=-3函数f(x)= x2–2x –3在[ 2,4 ]
上单调递增
探究3:函数f(x)= x2–2x –3在[ ]上的最值;截取图像对称轴x=1在[ ]内
函数f(x)= x2–2x –3在[ ]上先减后增得出最值
f( )= ,f(1)=-4 ,f( )=
= , =-4归纳3:对称轴 在区间[ a,b ] 内时,在端点或顶点处取得最值方法总结:求二次函数f(x)=ax2+bx+c在[m,n]上的最值: 方法一:
(1)画出图像(2)截取图像(3)得出最值
数形结合方法二:
(1)检查x0= 是否属于 [ m,n];
(2)当x0∈[m,n]时,f(m)、f(n)、f(x0)中的较大者是最大值,较小者是最小值;
(3)当x0 [m,n]时,f(m)、f(n)中的较大者是最大值,较小者是最小值.练习:求二次函数f(x)=x2-2ax-3在闭区间[3,4]上的最小值。解:如图可得:
1°当a<3时二次函数在[3,4]上单调递增
∴ f(x)min=f(3)=6-6a3°当a>4时,二次函数在[3,4]上单调递减∴ f(x)min=f(4)=13-8a
小结:求二次函数闭区间上的最值,含有参数时要分情况讨论,一般分对称轴在区间的左、中、右三种情况进行讨论yxo342°当3 a 4时二次函数先减后增
∴ f(x)min=f(a)=-a2-3学以致用谢谢各位光临指导
