1.1 锐角三角函数(第1课时)
图片预览


文档简介
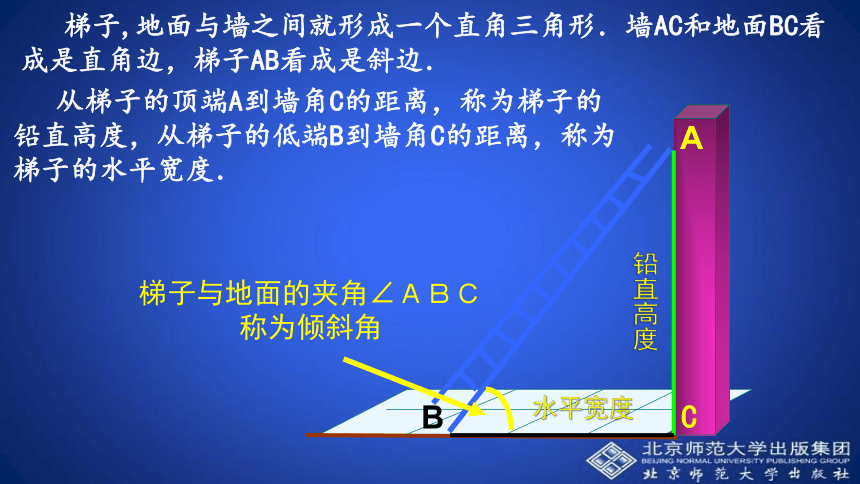
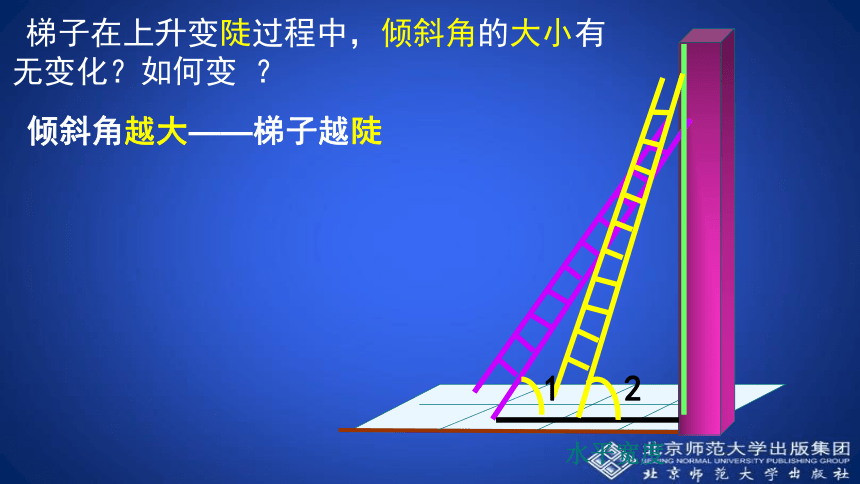
课件18张PPT。1.1 锐角三角函数(第1课时)第一章 直角三角形的边角关系梯子是我们日常生活中常见的物体.你知道梯子的倾斜程度与什么有关吗? 梯子,地面与墙之间就形成一个直角三角形.墙AC和地面BC看成是直角边,梯子AB看成是斜边.铅直高度水平宽度梯子与地面的夹角∠ABC称为倾斜角 从梯子的顶端A到墙角C的距离,称为梯子的铅直高度,从梯子的低端B到墙角C的距离,称为梯子的水平宽度. ACB 梯子在上升变陡过程中,倾斜角的大小有无变化?如何变 ?
水平宽度
12倾斜角越大——梯子越陡
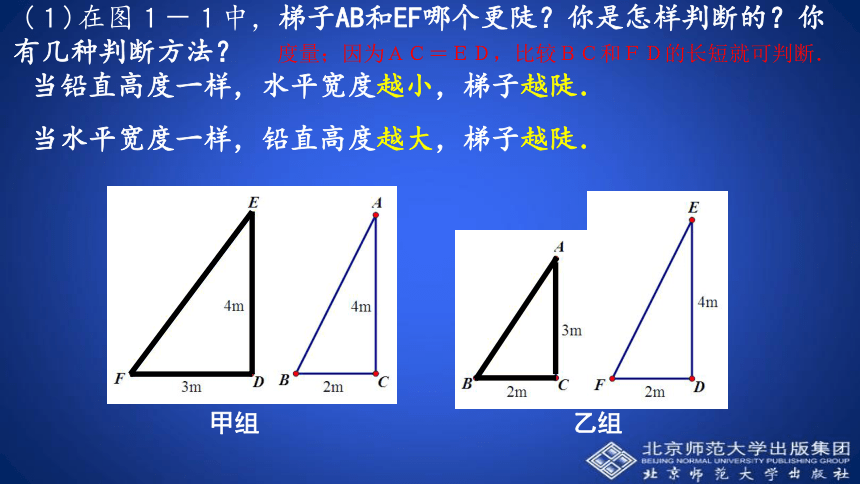
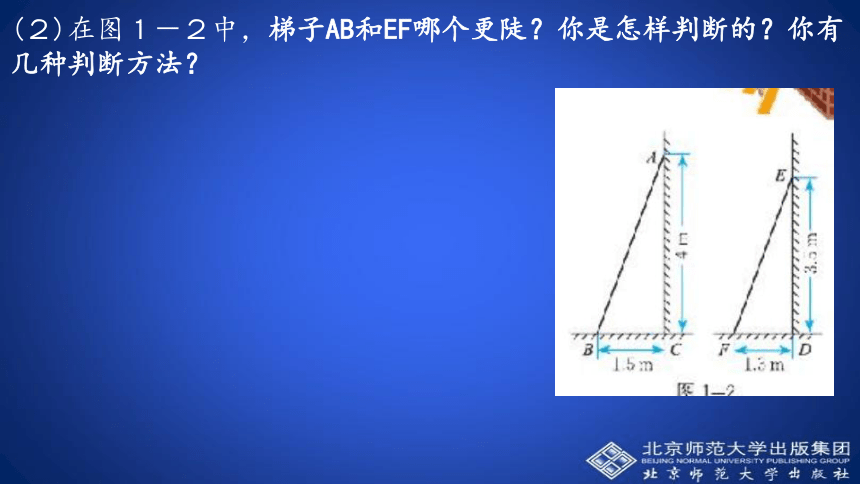
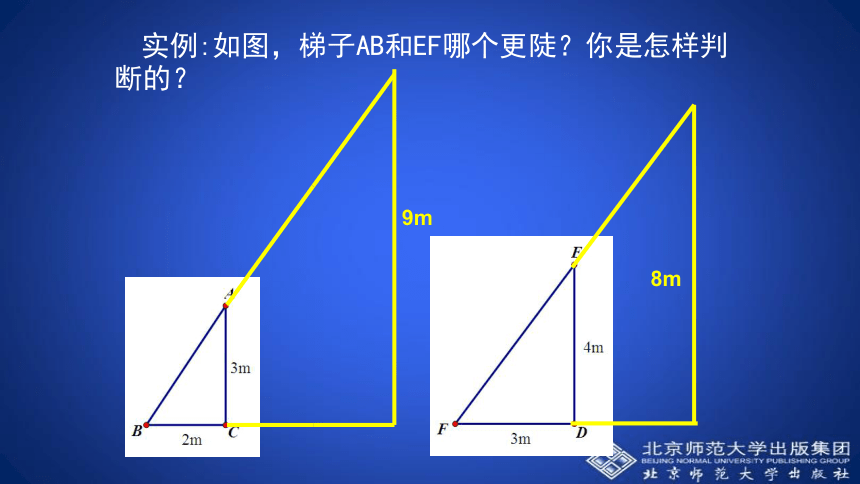
(1)在图1-1中,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法?当铅直高度一样,水平宽度越小,梯子越陡.当水平宽度一样,铅直高度越大,梯子越陡.甲组乙组度量;因为AC=ED,比较BC和FD的长短就可判断.(2)在图1-2中,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法? 实例:如图,梯子AB和EF哪个更陡?你是怎样判断的?9m8m如图,三部梯子的倾斜程度一样,通过测量发现其中两部梯子的数据如下,请你用上面的方法分析当倾斜角相等时,铅直高度和水平宽度之间有何关系。请你判别下列哪部梯子最陡记作:tanA梯子的倾斜程度与tanA的关系
tanA越大,梯子越陡, ∠A越大斜边∠A的对边BC∠A的邻边AC在Rt△ABC中1.tanA是在直角三角形中定义的,∠A是一个锐
角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯
省去“∠”号(注意tanA不表示tan乘以A).
3.tanA没有单位,它表示一个比值,即直角三角形中∠A的对边与邻边的比. 4.tanA的大小只与∠A的大小有关,而与直角三角
形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,
则这两个锐角相等.
请你用不同的符号表示下列图形中两个锐角的正切例1 下图表示两个自动扶梯的几何模型,那一个自动扶梯比较陡?解:甲梯中乙梯中∵ tanα> tanβ
∴甲梯更陡斜坡的倾斜程度常用坡度表示.例如,有一山坡在水平方向上每前进80m就升高60m,山坡的坡度
1.坡面与水平面的夹角(α)叫坡角
2.坡面的铅直高度与水平宽度的比称为坡度i
(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
例: 如图,为拦水坝的横截面,其中AB面的坡度
i= ,若坝高BC=20米,求坝面AB的长。这节课学习了哪些内容?在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫做∠A的正切.记作:tanA
tanA=
∠A的对边∠A的邻边∠A的对边∠A的邻边tanA越大,梯子越陡, ∠A越大课堂小结:作业布置习题1.1 1、2、4
课堂练习
12倾斜角越大——梯子越陡
(1)在图1-1中,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法?当铅直高度一样,水平宽度越小,梯子越陡.当水平宽度一样,铅直高度越大,梯子越陡.甲组乙组度量;因为AC=ED,比较BC和FD的长短就可判断.(2)在图1-2中,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法? 实例:如图,梯子AB和EF哪个更陡?你是怎样判断的?9m8m如图,三部梯子的倾斜程度一样,通过测量发现其中两部梯子的数据如下,请你用上面的方法分析当倾斜角相等时,铅直高度和水平宽度之间有何关系。请你判别下列哪部梯子最陡记作:tanA梯子的倾斜程度与tanA的关系
tanA越大,梯子越陡, ∠A越大斜边∠A的对边BC∠A的邻边AC在Rt△ABC中1.tanA是在直角三角形中定义的,∠A是一个锐
角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯
省去“∠”号(注意tanA不表示tan乘以A).
3.tanA没有单位,它表示一个比值,即直角三角形中∠A的对边与邻边的比. 4.tanA的大小只与∠A的大小有关,而与直角三角
形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,
则这两个锐角相等.
请你用不同的符号表示下列图形中两个锐角的正切例1 下图表示两个自动扶梯的几何模型,那一个自动扶梯比较陡?解:甲梯中乙梯中∵ tanα> tanβ
∴甲梯更陡斜坡的倾斜程度常用坡度表示.例如,有一山坡在水平方向上每前进80m就升高60m,山坡的坡度
1.坡面与水平面的夹角(α)叫坡角
2.坡面的铅直高度与水平宽度的比称为坡度i
(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
例: 如图,为拦水坝的横截面,其中AB面的坡度
i= ,若坝高BC=20米,求坝面AB的长。这节课学习了哪些内容?在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比随之确定,这个比叫做∠A的正切.记作:tanA
tanA=
∠A的对边∠A的邻边∠A的对边∠A的邻边tanA越大,梯子越陡, ∠A越大课堂小结:作业布置习题1.1 1、2、4
课堂练习
