1.1 锐角三角函数(第2课时)
图片预览




文档简介
课件15张PPT。第一章 直角三角形的边角关系1.1 锐角三角函数(第2课时)复习引入 2.在Rt△ABC中,∠C=90°,
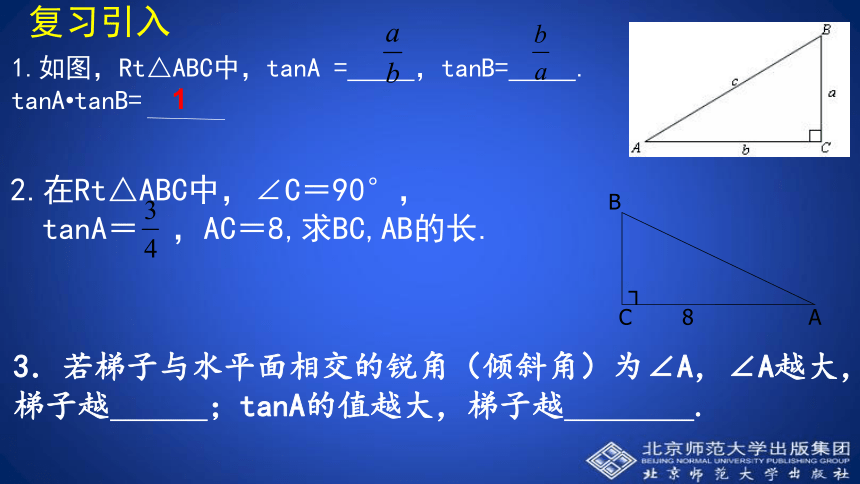
tanA= ,AC=8,求BC,AB的长.1.如图,Rt△ABC中,tanA = ,tanB= .
tanA?tanB= 3.若梯子与水平面相交的锐角(倾斜角)为∠A,∠A越大,梯子越 ;tanA的值越大,梯子越 .1探究活动1:如图 (1)Rt△AB1C1和Rt△AB2C2的关系是 . . (3)如果改变B2在斜边上的位置, .思考:从上面的问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值________,根据是___________________________.它的邻边与斜边的比值呢?思考:当Rt△ABC中的一个锐角A确定时,∠A的对边与邻边的比便随
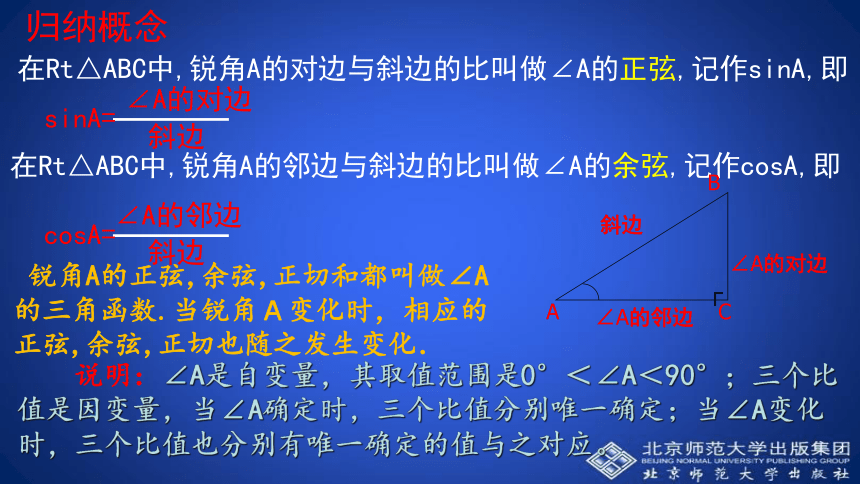
之确定.此时,其它边之间的比值也确定吗? 与同伴进行交流.也随之确定相似三角形的对应边成比例归纳概念在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即 锐角A的正弦,余弦,正切和都叫做∠A的三角函数.当锐角A变化时,相应的正弦,余弦,正切也随之发生变化. 说明:∠A是自变量,其取值范围是0°<∠A<90°;三个比值是因变量,当∠A确定时,三个比值分别唯一确定;当∠A变化时,三个比值也分别有唯一确定的值与之对应。铅直高度水平宽度倾斜角探究活动2:我们知道,梯子的倾斜程度与tanA有关系,tanA越大,梯子越陡,那么梯子的倾斜程度与sinA和cosA有关系吗?是怎样的关系?A探索发现:
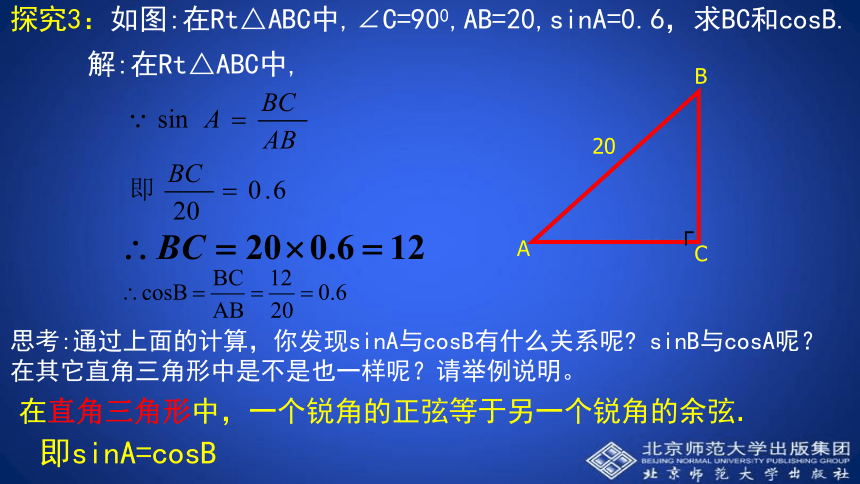
梯子的倾斜程度与sinA和cosA有关.sinA的值越大,梯子 ;cosA的值越 ,梯子越陡.越陡小探究3:如图:在Rt△ABC中,∠C=900,AB=20,sinA=0.6,求BC和cosB.解:在Rt△ABC中, 思考:通过上面的计算,你发现sinA与cosB有什么关系呢? sinB与cosA呢?在其它直角三角形中是不是也一样呢?请举例说明。在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.即sinA=cosB1、如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定2、已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.c==及时检测3、如图, ∠C=90°CD⊥ABACCDABADBCAC归类提升 类型一:已知直角三角形两边长,求锐角三角函数值.例1 如图,在Rt△ABC中,∠C=90°, AC=3,AB=6,求∠B的三个三角函数值。3 类型二:利用三角函数值求线段的长度例2 如图,在Rt△ABC中,∠C=90°,BC=5,sinA= ,求AC和AB。类型三:利用已知三角函数值,求其它三角函数值例3 在Rt△ABC中,∠C=90°,BC=6,sinA= ,求cosA、tanB的值. 类型四:求非直角三角形中锐角的三角函数值例4 如图:在等腰△ABC中,AB=AC=5,BC=6.求: sinB,cosB,tanB.求锐角三角函数时,勾股定理的运用是很重要的.1、锐角三角函数定义:
sinA= ,cosA= ,tanA= ;总结延伸sinB= ,cosB= ,tanB= ;2.若∠A+∠B=90°,则
(1)sinA=cosB,cosA=sinB,在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.(2)sinA2+sinB2=
(3)tanA·tanB=
(4)tanA=2、温馨提示:
(1)sinA,cosA,tanA, 是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形);
(2)sinA,cosA,tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
(3)sinA,cosA,tanA都是一个比值,注意区别,且sinA,cosA,tanA均大于0,无单位;
(4)sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长没有必然关系;
(5)角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.3.在用三角函数解决一般三角形或四边形的实际问题中,应注意构造直角三角形.
tanA= ,AC=8,求BC,AB的长.1.如图,Rt△ABC中,tanA = ,tanB= .
tanA?tanB= 3.若梯子与水平面相交的锐角(倾斜角)为∠A,∠A越大,梯子越 ;tanA的值越大,梯子越 .1探究活动1:如图 (1)Rt△AB1C1和Rt△AB2C2的关系是 . . (3)如果改变B2在斜边上的位置, .思考:从上面的问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值________,根据是___________________________.它的邻边与斜边的比值呢?思考:当Rt△ABC中的一个锐角A确定时,∠A的对边与邻边的比便随
之确定.此时,其它边之间的比值也确定吗? 与同伴进行交流.也随之确定相似三角形的对应边成比例归纳概念在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即 锐角A的正弦,余弦,正切和都叫做∠A的三角函数.当锐角A变化时,相应的正弦,余弦,正切也随之发生变化. 说明:∠A是自变量,其取值范围是0°<∠A<90°;三个比值是因变量,当∠A确定时,三个比值分别唯一确定;当∠A变化时,三个比值也分别有唯一确定的值与之对应。铅直高度水平宽度倾斜角探究活动2:我们知道,梯子的倾斜程度与tanA有关系,tanA越大,梯子越陡,那么梯子的倾斜程度与sinA和cosA有关系吗?是怎样的关系?A探索发现:
梯子的倾斜程度与sinA和cosA有关.sinA的值越大,梯子 ;cosA的值越 ,梯子越陡.越陡小探究3:如图:在Rt△ABC中,∠C=900,AB=20,sinA=0.6,求BC和cosB.解:在Rt△ABC中, 思考:通过上面的计算,你发现sinA与cosB有什么关系呢? sinB与cosA呢?在其它直角三角形中是不是也一样呢?请举例说明。在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.即sinA=cosB1、如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定2、已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.c==及时检测3、如图, ∠C=90°CD⊥ABACCDABADBCAC归类提升 类型一:已知直角三角形两边长,求锐角三角函数值.例1 如图,在Rt△ABC中,∠C=90°, AC=3,AB=6,求∠B的三个三角函数值。3 类型二:利用三角函数值求线段的长度例2 如图,在Rt△ABC中,∠C=90°,BC=5,sinA= ,求AC和AB。类型三:利用已知三角函数值,求其它三角函数值例3 在Rt△ABC中,∠C=90°,BC=6,sinA= ,求cosA、tanB的值. 类型四:求非直角三角形中锐角的三角函数值例4 如图:在等腰△ABC中,AB=AC=5,BC=6.求: sinB,cosB,tanB.求锐角三角函数时,勾股定理的运用是很重要的.1、锐角三角函数定义:
sinA= ,cosA= ,tanA= ;总结延伸sinB= ,cosB= ,tanB= ;2.若∠A+∠B=90°,则
(1)sinA=cosB,cosA=sinB,在直角三角形中,一个锐角的正弦等于另一个锐角的余弦.(2)sinA2+sinB2=
(3)tanA·tanB=
(4)tanA=2、温馨提示:
(1)sinA,cosA,tanA, 是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形);
(2)sinA,cosA,tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
(3)sinA,cosA,tanA都是一个比值,注意区别,且sinA,cosA,tanA均大于0,无单位;
(4)sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长没有必然关系;
(5)角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.3.在用三角函数解决一般三角形或四边形的实际问题中,应注意构造直角三角形.
